苏科版七年级下册数学课件9.1—9.4 复习课(共19张PPT)
文档属性
| 名称 | 苏科版七年级下册数学课件9.1—9.4 复习课(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 10:17:40 | ||
图片预览





文档简介
第9章 9.1~9.4 复习课
苏教版七年级下册 数学
知识回顾:
1、单项式乘单项式
2、单项式乘多项式
3、多项式乘多项式
4、完全平方公式
5、平方差公式
一般
特殊
简
难
① 系数相乘的结果作为系数
② 同底数幂相乘
③ 只在一个单项式中含有的字母,
连同指数作为积的一个因式
单项式 单项式
×
知识点一:
单项式 单项式
×
知识点一:
1. (-3a2b3)2.(-2a3b2)3=
原式=9a4b6.(-8a9b6)
=(-8×9)(a4.a9)(b6.b6)
=-72a13b12
-72a13b12
2. (-x2ym)2.(kxn+1y) =-2x6y3,则k= ,m= ,
n= 。
原式=x4y2m .(kxn+1y)
=k(x4.xn+1)(y2m.y)
=kxn+5y2m+1
1
-2
1
单项式 多项式
×
知识点二:
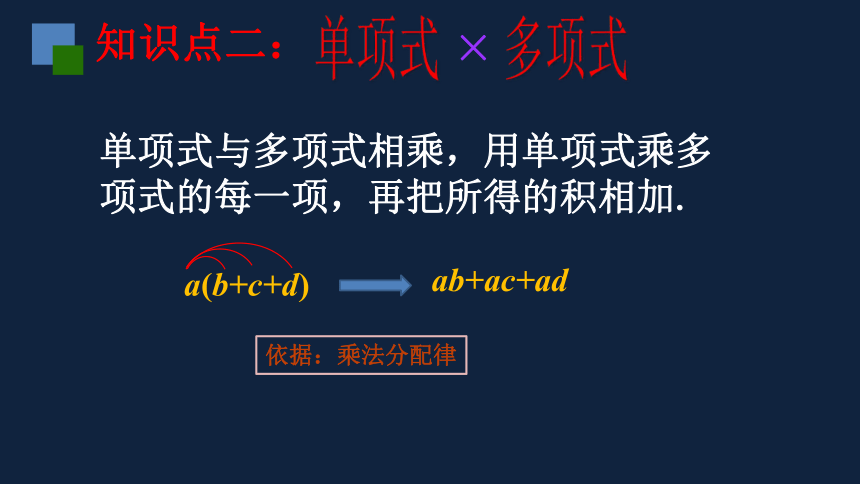
单项式与多项式相乘,用单项式乘多项式的每一项,再把所得的积相加.
ab+ac+ad
a(b+c+d)
依据:乘法分配律
单项式 多项式
×
知识点二:
3.(-2a3+3a2-4a).(-5a5)=
10a8-15a7+20a6
注意变号
4. 已知xy2=-2,则-xy(x2y5-xy3-y)的值为( )
A.2 B.6 C.10 D.14
解:原式=-x3y6+x2y4+xy2
=-(xy2)3+(xy2)2+xy2
∵xy2=-2,
∴原式=-(-2)3+(-2)2+(-2)=8+4-2=10
C
整体代入
(a+b)(c+d)
多项式 多项式
×
知识点三:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
ac+bc+ad+bd
多项式 多项式
×
知识点三:
6. 若a-b=1,ab=-2,则(a+1).(b-1)= 。
原式=x2-4x-bx+4b
=x2-(4+b)x+4b
展开
合并同类项
整体代入
注意变号
-3
-4
5. (x-4).(x-b)= x2-x+a,则a= ,b= 。
原式=ab-a+b-1
=ab-(a-b)-1
当a-b=1,ab=-2时,
原式=-2-1-1=-4
展开
添括号
整体思想
-12
添括号
多项式 多项式
×
知识点三:
7. 多项式x2+x+b与多项式x2-ax-2的乘积不含x2项
和x3项,则-????(?????????????)的值是
?
解: (x2+x+b)(x2-ax-2)
=x4-ax3-2x2+x3-ax2-2x+bx2-abx-2b
=x4+(-a+1)x3+(-2-a+b)x2+(-2-ab)x-2b
∵不含x2项和x3项
∴
?????+1=0?2?????+????=0
?
∴
????=1????=3
?
0
展开
合并同类项
完全平方式
知识点四:
语言表述:两数和(差)的平方,等于它们的平方和加上(减去)它们乘积的两倍.
(a-b)2 a2-2ab+b2
(a+b)2 a2+2ab+b2
符号看前方
完全平方式
知识点四:
8. 已知a+b=2,ab=1,求:
(1)a2+b2
(a-b)2=a2-2ab+b2
(a+b)2=a2+2ab+b2
整体思想
解:∵a+b=2
∴(a+b)2=a2+2ab+b2
=4
∵ab=1
∴a2+b2=4-2=2
完全平方式
知识点四:
8. 已知a+b=2,ab=1,求:
(2)a2+b2-3ab
(a-b)2=a2-2ab+b2
(a+b)2=a2+2ab+b2
解:由(1)得:a2+b2=2
又∵ab=1
∴a2+b2-3ab=2-3=-1
方法二
a2+b2-3ab=(a+b)2-5ab
=22-5×1
=-1
方法一
完全平方式
知识点四:
8. 已知a+b=2,ab=1,求:
(3)(a-b)2
(a-b)2=a2-2ab+b2
(a+b)2=a2+2ab+b2
解:∵a+b=2
∴(a-b)2=(a+b)2-4ab
=22-4×1
=0
整体思想
完全平方式
知识点四:
(a-b)2=a2+b2-2ab
(a+b)2=a2+b2+2ab
整体思想
9. 若n满足(n-2004)2+(2005-n)2=1,则
(2005-n) (n-2004) =
解:设n-2004=a,2005-n=b
则a2+b2=1,
又a+b=1,
挖掘隐含条件
∴2ab=(a+b)2-(a2+b2)=0
∴ab=0
即(2005-n) (n-2004) =0
0
平方差公式
知识点五:
(a+b)(a-b) a2-b2
语言表述:两个数的和与这两个数的差的积等于这两个数的平方差.
平方差公式
知识点五:
10.计算: (1) (a-b)(a+b)(a2-b2)
解:原式=(a2-b2)(a2-b2) =(a2-b2)2
=a4-2a2b2+b4
(2) (x-2y+2)(x+2y-2)
解:原式=[x-(2y-2)][x+(2y-2)]
=x2-(2y-2)2
=x2-(4y2-8y+4)
=x2-4y2+8y-4
整体思想
添括号
平方差公式
知识点五:
11.已知a+b=2,那么a2-b2+4b=
整体代入
(a+b)(a-b) =a2-b2
逆用
解:原式=(a+b)(a-b) +4b
=2(a-b)+4b
=2a-2b+4b
=2a+2b
=2(a+b)
=4
4
解: ∵ a+b=2
∴a=2-b
∴原式=(2-b)2-b2+4b
=4-4b+b2-b2+4b
=4
转化
整体代入
方法二
方法一
平方差公式
知识点五:
(2)20062-2005×2007
12. 计算 (1)832-172
解:原式=20062-(2006-1)(2006+1)
=20062-(20062-1)
=1
解:原式=(83-17)(83+17)
=66 ×100
=6600
(a+b)(a-b) =a2-b2
逆用
(2)将图③中的正方形分割,并填上相应的代数式,用拼图法可得出(a+b+c+d)2 =______________ _________
(3)通过上题的推导,你发现了什么规律?课后对代数式:(a+b+c+d+e)2 的展开式进行探索。
③
巩固练习,提高深化
a
a
b
b
c
c
d
d
+2ab+2ac+2ad+2bc+2bd+2cd
a2+ b2 +c2+d2
a2
b2
c2
d2
ab
ab
ac
ac
ad
ad
bc
bc
bd
bd
cd
cd
苏教版七年级下册 数学
知识回顾:
1、单项式乘单项式
2、单项式乘多项式
3、多项式乘多项式
4、完全平方公式
5、平方差公式
一般
特殊
简
难
① 系数相乘的结果作为系数
② 同底数幂相乘
③ 只在一个单项式中含有的字母,
连同指数作为积的一个因式
单项式 单项式
×
知识点一:
单项式 单项式
×
知识点一:
1. (-3a2b3)2.(-2a3b2)3=
原式=9a4b6.(-8a9b6)
=(-8×9)(a4.a9)(b6.b6)
=-72a13b12
-72a13b12
2. (-x2ym)2.(kxn+1y) =-2x6y3,则k= ,m= ,
n= 。
原式=x4y2m .(kxn+1y)
=k(x4.xn+1)(y2m.y)
=kxn+5y2m+1
1
-2
1
单项式 多项式
×
知识点二:
单项式与多项式相乘,用单项式乘多项式的每一项,再把所得的积相加.
ab+ac+ad
a(b+c+d)
依据:乘法分配律
单项式 多项式
×
知识点二:
3.(-2a3+3a2-4a).(-5a5)=
10a8-15a7+20a6
注意变号
4. 已知xy2=-2,则-xy(x2y5-xy3-y)的值为( )
A.2 B.6 C.10 D.14
解:原式=-x3y6+x2y4+xy2
=-(xy2)3+(xy2)2+xy2
∵xy2=-2,
∴原式=-(-2)3+(-2)2+(-2)=8+4-2=10
C
整体代入
(a+b)(c+d)
多项式 多项式
×
知识点三:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
ac+bc+ad+bd
多项式 多项式
×
知识点三:
6. 若a-b=1,ab=-2,则(a+1).(b-1)= 。
原式=x2-4x-bx+4b
=x2-(4+b)x+4b
展开
合并同类项
整体代入
注意变号
-3
-4
5. (x-4).(x-b)= x2-x+a,则a= ,b= 。
原式=ab-a+b-1
=ab-(a-b)-1
当a-b=1,ab=-2时,
原式=-2-1-1=-4
展开
添括号
整体思想
-12
添括号
多项式 多项式
×
知识点三:
7. 多项式x2+x+b与多项式x2-ax-2的乘积不含x2项
和x3项,则-????(?????????????)的值是
?
解: (x2+x+b)(x2-ax-2)
=x4-ax3-2x2+x3-ax2-2x+bx2-abx-2b
=x4+(-a+1)x3+(-2-a+b)x2+(-2-ab)x-2b
∵不含x2项和x3项
∴
?????+1=0?2?????+????=0
?
∴
????=1????=3
?
0
展开
合并同类项
完全平方式
知识点四:
语言表述:两数和(差)的平方,等于它们的平方和加上(减去)它们乘积的两倍.
(a-b)2 a2-2ab+b2
(a+b)2 a2+2ab+b2
符号看前方
完全平方式
知识点四:
8. 已知a+b=2,ab=1,求:
(1)a2+b2
(a-b)2=a2-2ab+b2
(a+b)2=a2+2ab+b2
整体思想
解:∵a+b=2
∴(a+b)2=a2+2ab+b2
=4
∵ab=1
∴a2+b2=4-2=2
完全平方式
知识点四:
8. 已知a+b=2,ab=1,求:
(2)a2+b2-3ab
(a-b)2=a2-2ab+b2
(a+b)2=a2+2ab+b2
解:由(1)得:a2+b2=2
又∵ab=1
∴a2+b2-3ab=2-3=-1
方法二
a2+b2-3ab=(a+b)2-5ab
=22-5×1
=-1
方法一
完全平方式
知识点四:
8. 已知a+b=2,ab=1,求:
(3)(a-b)2
(a-b)2=a2-2ab+b2
(a+b)2=a2+2ab+b2
解:∵a+b=2
∴(a-b)2=(a+b)2-4ab
=22-4×1
=0
整体思想
完全平方式
知识点四:
(a-b)2=a2+b2-2ab
(a+b)2=a2+b2+2ab
整体思想
9. 若n满足(n-2004)2+(2005-n)2=1,则
(2005-n) (n-2004) =
解:设n-2004=a,2005-n=b
则a2+b2=1,
又a+b=1,
挖掘隐含条件
∴2ab=(a+b)2-(a2+b2)=0
∴ab=0
即(2005-n) (n-2004) =0
0
平方差公式
知识点五:
(a+b)(a-b) a2-b2
语言表述:两个数的和与这两个数的差的积等于这两个数的平方差.
平方差公式
知识点五:
10.计算: (1) (a-b)(a+b)(a2-b2)
解:原式=(a2-b2)(a2-b2) =(a2-b2)2
=a4-2a2b2+b4
(2) (x-2y+2)(x+2y-2)
解:原式=[x-(2y-2)][x+(2y-2)]
=x2-(2y-2)2
=x2-(4y2-8y+4)
=x2-4y2+8y-4
整体思想
添括号
平方差公式
知识点五:
11.已知a+b=2,那么a2-b2+4b=
整体代入
(a+b)(a-b) =a2-b2
逆用
解:原式=(a+b)(a-b) +4b
=2(a-b)+4b
=2a-2b+4b
=2a+2b
=2(a+b)
=4
4
解: ∵ a+b=2
∴a=2-b
∴原式=(2-b)2-b2+4b
=4-4b+b2-b2+4b
=4
转化
整体代入
方法二
方法一
平方差公式
知识点五:
(2)20062-2005×2007
12. 计算 (1)832-172
解:原式=20062-(2006-1)(2006+1)
=20062-(20062-1)
=1
解:原式=(83-17)(83+17)
=66 ×100
=6600
(a+b)(a-b) =a2-b2
逆用
(2)将图③中的正方形分割,并填上相应的代数式,用拼图法可得出(a+b+c+d)2 =______________ _________
(3)通过上题的推导,你发现了什么规律?课后对代数式:(a+b+c+d+e)2 的展开式进行探索。
③
巩固练习,提高深化
a
a
b
b
c
c
d
d
+2ab+2ac+2ad+2bc+2bd+2cd
a2+ b2 +c2+d2
a2
b2
c2
d2
ab
ab
ac
ac
ad
ad
bc
bc
bd
bd
cd
cd
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
