苏科版数学八年级下册10.1分式课件(共22张PPT)
文档属性
| 名称 | 苏科版数学八年级下册10.1分式课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 10:20:20 | ||
图片预览








文档简介
第10章 分式 10.1 分式
苏科版八年级下册 数学
我们知道:我们每课时学习的数学知识是相对独立的。但实际上,所有数学知识是联系的,整体的。
把这些“知识点” 联系起来看就组成了一条“知识线”。
把这些“知识线” 整体地看就组成了一个“知识面”。最终组成数学的知识结构和知识体系。
所以建议同学们在每天学习数学之前,最好养成这样的习惯,站在今天要学知识的视角,看看昨天学了什么,想想明天会学什么?只有这样联系地学,整体地学,你才会学得更好!
一、我们从哪里来?现在在哪里?
1.小学里的“算术数”引进“负数”走到初中里的“有理数”,完成了代数的第一次飞跃!
2.初中里的“数”用“字母表示数”走到初中里的“式 ”,从特殊到一般,完成了代数的第二次飞跃!
3.
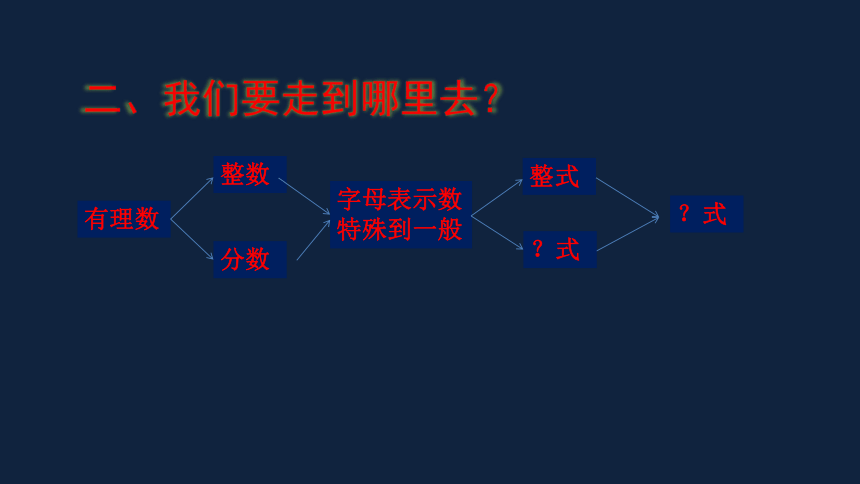
有理数
整数
分数
字母表示数
特殊到一般
整式
运算:加减乘
有理数
整数
分数
字母表示数
特殊到一般
整式
?式
?式
二、我们要走到哪里去?
三、我们怎样走到那里去?
解决数学内部的矛盾
解决遇到的实际问题
数学的发展
(一)数学视角
整式的运算只研究了加减、乘法(乘方)运算,如果进行除法运算,会怎样?
问题1:a4÷a2=?
问题2:a2÷a4=?
解答1:a4÷a2=a2(同底数幂的除法)
解答2:a2÷a4=a-2= (负整数指数幂定义)
问题1:
(1)如果某市人口总数为650万人,绿地总面积为 b m2,那么该市人均拥有绿地面积为( )m2;
(2)如果某市人口总数为a人,绿地总面积为b m2,那么该市人均拥有绿地面积为( ) m2 ;
(二)生活视角
(2)一块长方形玻璃的面积为s m2,如果长
是 12m,那么宽是( )m.
(3)一块长方形玻璃的面积为s m2,如果长
是 a m,那么宽是( )m.
问题2:
(1)一块长方形玻璃的面积为5 m2,如果
长是3 m,那么宽是( )m.
问题3:
有两块棉田,一块面积为a 公顷,产棉花m 千克;另一块面积为b 公顷,产棉花n 千克. 这两块棉田平均每公顷产棉花( )千克.
b 公顷
a 公顷
类比联想
这些式子有什么共同点和不同点?
相同点:1.都具有分数线,具有分数的形式。
不同点:前面3个代数式就是整式,后4个代数式,分母中都含有字母,不是整式。
2.分子或者分母都是整式。
归纳抽象
一般地,如果A、B表示两个整式,并且B中含有字母,那么代数式 叫做分式,其中A是分式的分子,B是分式的分母.
分式的定义
……
现学即用
下列代数式中,哪些是分式?并说明理由.
答:分式有(2)、(5)、(6).
理由:形如 ,A、B为整式,且B中含有字母.
深化认识
在分式 中,因为B中含有字母,根据小学知识就可以知道分母(除数)不能为0,所以,说到分式,首先要考虑的是分母的情况。
分母B ≠0,分式有意义
分式
分母B =0,分式无意义
运用知识
例1.当x取什么值时,分式
(1)无意义?(2)有意义?
解:由分母2x-3=0 ,得 ,所以当 时,
分式无意义;当 时,分式有意义.
总结:分式有意义、无意义只跟分式的分母有关。
例2.当x取什么值时,分式 的值为零?
分析:分式属于代数式,根据代数式的知识,分式的值随分式中字母取值的变化而变化。用具体的数值代替分式中的字母,按照式子中的运算关系计算,就能得到相应的分式的值。求分式的值的前提是分母不等于0.
总结:1.考虑到不等式求解的困难,我们也可以先分子等于0,求出x的值后,再代入分母检验是否等于0。
2.如果上面问题变成“分式的值为-2”,你会列式吗?
3.分式的值为0,首先是分母B ≠0,其次是分子A=0。
解:由条件可知,分母2x-3 ≠ 0且分子x-2=0 ,得 ,且x=2,所以,当x=2时,分式的值为零.
思维拓展
值为正?
例3.当x取什么值时,分式
分析:根据“两数相除,同号得正,异号得负”得到不等式组,不等式组的解集就是要求的x的取值范围.
变式:若上述“分式的值为负”呢,同学们会求吗?
分式可以表示现实生活中的一些数量关系!
提高认识
1.b个苹果分给a个孩子,每个孩子分到 个?
2.a亩地的总产量是b公斤,每亩平均产量 公斤?
3.b元钱买了a支铅笔,每支 元?
4.……………………………………
你还能对分式 所表示的意义做出解释吗?
小结:分式(代数式):符号语言!具有一般性!有效模型!
整式
定义
运算:整式的加减、整式的乘法
四、后面我们将走向哪里?
分数
定义
分数的基本性质
约分、通分、计算
分式
定义
???
来路——思路——去路
通过今天这节课的学习和研究,你有哪些收获?
1.知道了分式的定义和分式的值的定义;特别要注意B ≠0的前提;
2.知道了分式从哪里来,向哪里去?
3.知道了研究分式的一般方法和学习路径。
课堂小结
1.阅读本课教材;
2.体会学习方法;
3.完成巩固练习。
课后作业
感谢大家
当堂练习
1(1)小明t小时走了s千米的路,则小明走路的平均速度是( )千米/小时;
(2)一件工作甲单独做需a天完成,乙单独做需b天完成,甲乙合作1天完成的工作量为( ).
2(1)当a 时,分式 无意义;
(2)当a 时,分式 有意义;
(3)当a 时,分式 的值为0.
3.若分式 的值为负数,求x的取值范围.
4.当x为何整数时,分式 的值为整数?
苏科版八年级下册 数学
我们知道:我们每课时学习的数学知识是相对独立的。但实际上,所有数学知识是联系的,整体的。
把这些“知识点” 联系起来看就组成了一条“知识线”。
把这些“知识线” 整体地看就组成了一个“知识面”。最终组成数学的知识结构和知识体系。
所以建议同学们在每天学习数学之前,最好养成这样的习惯,站在今天要学知识的视角,看看昨天学了什么,想想明天会学什么?只有这样联系地学,整体地学,你才会学得更好!
一、我们从哪里来?现在在哪里?
1.小学里的“算术数”引进“负数”走到初中里的“有理数”,完成了代数的第一次飞跃!
2.初中里的“数”用“字母表示数”走到初中里的“式 ”,从特殊到一般,完成了代数的第二次飞跃!
3.
有理数
整数
分数
字母表示数
特殊到一般
整式
运算:加减乘
有理数
整数
分数
字母表示数
特殊到一般
整式
?式
?式
二、我们要走到哪里去?
三、我们怎样走到那里去?
解决数学内部的矛盾
解决遇到的实际问题
数学的发展
(一)数学视角
整式的运算只研究了加减、乘法(乘方)运算,如果进行除法运算,会怎样?
问题1:a4÷a2=?
问题2:a2÷a4=?
解答1:a4÷a2=a2(同底数幂的除法)
解答2:a2÷a4=a-2= (负整数指数幂定义)
问题1:
(1)如果某市人口总数为650万人,绿地总面积为 b m2,那么该市人均拥有绿地面积为( )m2;
(2)如果某市人口总数为a人,绿地总面积为b m2,那么该市人均拥有绿地面积为( ) m2 ;
(二)生活视角
(2)一块长方形玻璃的面积为s m2,如果长
是 12m,那么宽是( )m.
(3)一块长方形玻璃的面积为s m2,如果长
是 a m,那么宽是( )m.
问题2:
(1)一块长方形玻璃的面积为5 m2,如果
长是3 m,那么宽是( )m.
问题3:
有两块棉田,一块面积为a 公顷,产棉花m 千克;另一块面积为b 公顷,产棉花n 千克. 这两块棉田平均每公顷产棉花( )千克.
b 公顷
a 公顷
类比联想
这些式子有什么共同点和不同点?
相同点:1.都具有分数线,具有分数的形式。
不同点:前面3个代数式就是整式,后4个代数式,分母中都含有字母,不是整式。
2.分子或者分母都是整式。
归纳抽象
一般地,如果A、B表示两个整式,并且B中含有字母,那么代数式 叫做分式,其中A是分式的分子,B是分式的分母.
分式的定义
……
现学即用
下列代数式中,哪些是分式?并说明理由.
答:分式有(2)、(5)、(6).
理由:形如 ,A、B为整式,且B中含有字母.
深化认识
在分式 中,因为B中含有字母,根据小学知识就可以知道分母(除数)不能为0,所以,说到分式,首先要考虑的是分母的情况。
分母B ≠0,分式有意义
分式
分母B =0,分式无意义
运用知识
例1.当x取什么值时,分式
(1)无意义?(2)有意义?
解:由分母2x-3=0 ,得 ,所以当 时,
分式无意义;当 时,分式有意义.
总结:分式有意义、无意义只跟分式的分母有关。
例2.当x取什么值时,分式 的值为零?
分析:分式属于代数式,根据代数式的知识,分式的值随分式中字母取值的变化而变化。用具体的数值代替分式中的字母,按照式子中的运算关系计算,就能得到相应的分式的值。求分式的值的前提是分母不等于0.
总结:1.考虑到不等式求解的困难,我们也可以先分子等于0,求出x的值后,再代入分母检验是否等于0。
2.如果上面问题变成“分式的值为-2”,你会列式吗?
3.分式的值为0,首先是分母B ≠0,其次是分子A=0。
解:由条件可知,分母2x-3 ≠ 0且分子x-2=0 ,得 ,且x=2,所以,当x=2时,分式的值为零.
思维拓展
值为正?
例3.当x取什么值时,分式
分析:根据“两数相除,同号得正,异号得负”得到不等式组,不等式组的解集就是要求的x的取值范围.
变式:若上述“分式的值为负”呢,同学们会求吗?
分式可以表示现实生活中的一些数量关系!
提高认识
1.b个苹果分给a个孩子,每个孩子分到 个?
2.a亩地的总产量是b公斤,每亩平均产量 公斤?
3.b元钱买了a支铅笔,每支 元?
4.……………………………………
你还能对分式 所表示的意义做出解释吗?
小结:分式(代数式):符号语言!具有一般性!有效模型!
整式
定义
运算:整式的加减、整式的乘法
四、后面我们将走向哪里?
分数
定义
分数的基本性质
约分、通分、计算
分式
定义
???
来路——思路——去路
通过今天这节课的学习和研究,你有哪些收获?
1.知道了分式的定义和分式的值的定义;特别要注意B ≠0的前提;
2.知道了分式从哪里来,向哪里去?
3.知道了研究分式的一般方法和学习路径。
课堂小结
1.阅读本课教材;
2.体会学习方法;
3.完成巩固练习。
课后作业
感谢大家
当堂练习
1(1)小明t小时走了s千米的路,则小明走路的平均速度是( )千米/小时;
(2)一件工作甲单独做需a天完成,乙单独做需b天完成,甲乙合作1天完成的工作量为( ).
2(1)当a 时,分式 无意义;
(2)当a 时,分式 有意义;
(3)当a 时,分式 的值为0.
3.若分式 的值为负数,求x的取值范围.
4.当x为何整数时,分式 的值为整数?
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
