苏科版数学八年级下册9.5三角形的中位线课件(共22张PPT)
文档属性
| 名称 | 苏科版数学八年级下册9.5三角形的中位线课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 10:21:54 | ||
图片预览





文档简介
9.5 三角形中位线
苏科版八年级下册 数学
动手操作
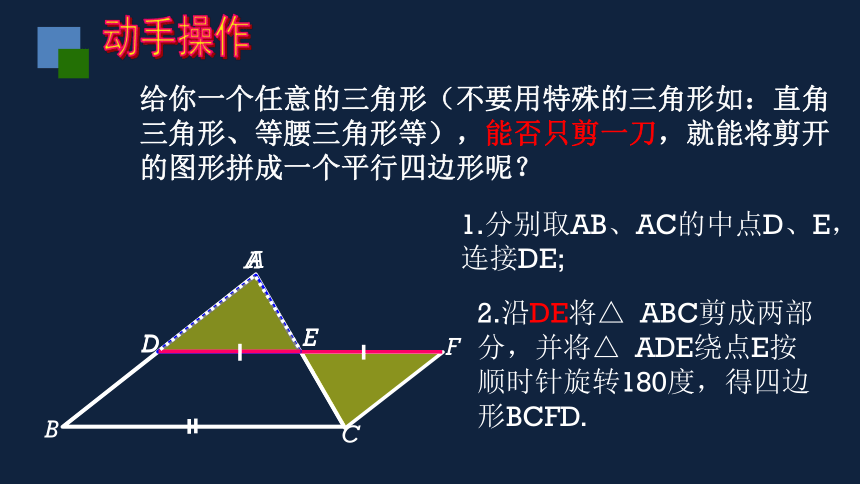
给你一个任意的三角形(不要用特殊的三角形如:直角三角形、等腰三角形等),能否只剪一刀,就能将剪开的图形拼成一个平行四边形呢?
A
B
C
D
E
A
D
E
F
1.分别取AB、AC的中点D、E,连接DE;
2.沿DE将△ ABC剪成两部分,并将△ ADE绕点E按顺时针旋转180度,得四边形BCFD.
A
B
C
D
E
F
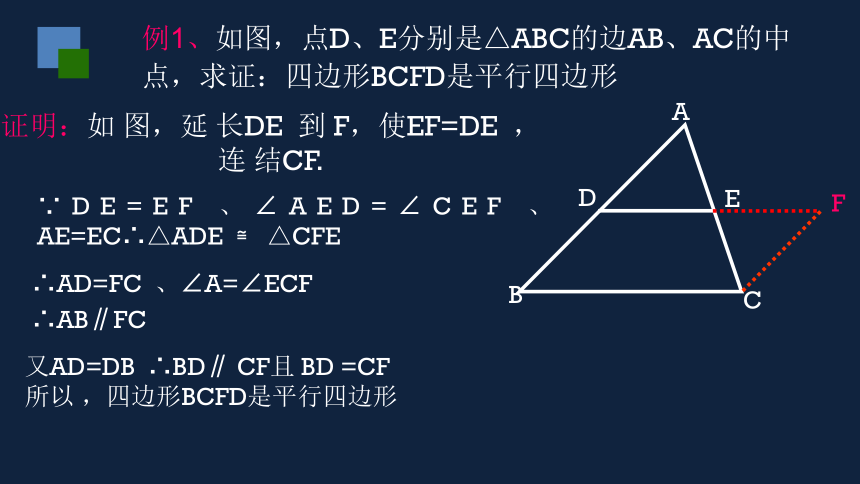
∵DE=EF 、∠AED=∠CEF 、AE=EC∴△ADE ≌ △CFE
证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∴AD=FC 、∠A=∠ECF
∴AB∥FC
又AD=DB ∴BD∥ CF且 BD =CF
所以 ,四边形BCFD是平行四边形
例1、如图,点D、E分别是△ABC的边AB、AC的中点,求证:四边形BCFD是平行四边形
F
E
思考:
1、一个三角形有几条中位线?
A
B
C
D
例如:DE是△ABC的中位线
三角形的中位线定义:
3条
四个
2、这三条中位线把三角形分成几个三角形?
连结三角形两边中点的线段叫三角形的中位线。
线段:DE、EF、DF
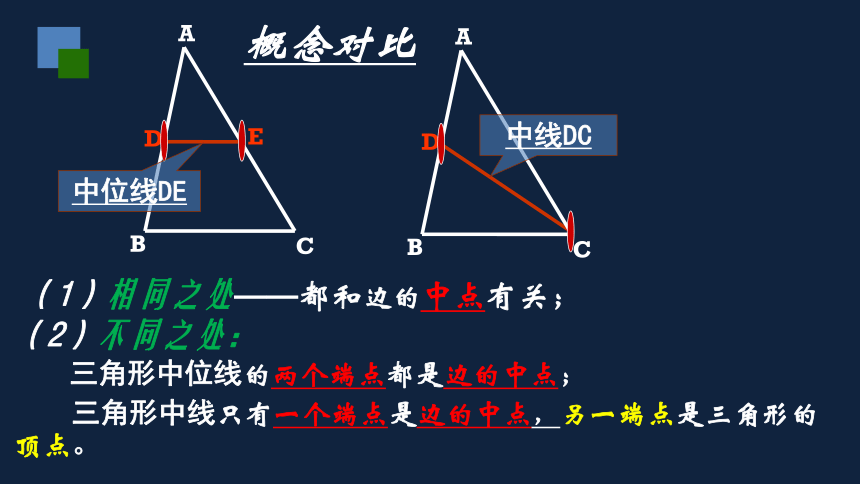
(1)相同之处——都和边的中点有关;
(2)不同之处:
三角形中位线的两个端点都是边的中点;
三角形中线只有一个端点是边的中点,另一端点是三角形的顶点。
C
B
A
E
D
概念对比
C
B
A
D
中线DC
中位线DE
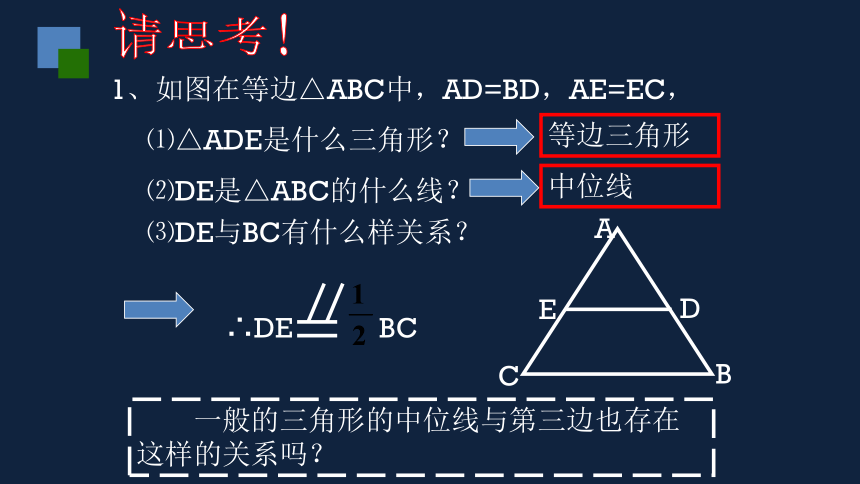
1、如图在等边△ABC中,AD=BD,AE=EC,
B
C
D
E
A
⑴△ADE是什么三角形?
⑶DE与BC有什么样关系?
等边三角形
请思考!
∴DE BC
一般的三角形的中位线与第三边也存在这样的关系吗?
⑵DE是△ABC的什么线?
中位线
又∵DE=EF ∠1=∠2
∴△ADE ≌ △CFE
证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∴AD=FC 、∠A=∠ECF
∴AB∥FC
又AD=DB
∴BD∥ CF且 BD =CF
∴四边形BCFD是平行四边形
还有另外的证法吗?
∴DF∥BC,DF=BC
又∵
即DE∥BC
∵点E是AC的中点∴AE=EC
例1、已知:在△ABC 中,DE是△ABC 的中位线
求证:DE∥BC,且DE= BC 。
A
B
C
D
E
F
1
2
⌒
⌒
A
B
C
E
D
F
证明:如图,延长DE至F,
使EF=DE,连接CD、AF、CF
∵AE=EC DE=EF
∴四边形ADCF是平行四边形
∴AD FC
又∵D为AB中点,
∴DB FC
∴四边形BCFD是平行四边形
∴DF= BC
//
又DE DF
∴DE= BC
∥
C
E
D
F
B
A
证法三:过点C作AB的平行线交DE的延长线于F
∵CF∥AB,
∴∠A=∠ECF
又AE=EC,∠AED=∠CEF
∴△ADE≌△CFE
∴ AD=FC
又DB=AD,∴DB = FC
∥
∴四边形BCFD是平行四边形
∴DE// BC 且DE=EF=1/2BC
三角形中位线定理
三角形的中位线平行于第三边,且等于第三边的一半。
C
A
B
D
E
用符号语言表示
∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.
2
1
(数量关系)
(位置关系)
主要用途:
(1)证明平行
(2)证明一条线段是另一条线段的2倍或
2.如图:在△ABC中,DE是中位线。
(1)若∠ADE=60°,则∠B= ;
(2)若BC=8cm,则DE= cm.
(3)DE +BC=12cm,则BC=
60°
4
8cm
6cm
1.三角形的中位线_______第三边,并且______第三边的_______
平行于
等于
一半
3.若等腰△ABC的周长40cm,AB=AC=14cm,则中位线DE=
E
A
B
C
D
4.如图, MN为△ABC的中位线,若∠ABC=61°则∠AMN= ,若MN=12,则BC= .
A
M
B
C
N
61°
24
5. 如图, △ABC中,D,E分别为AB,AC 的中点,当BC=10㎝时,则DE= .
5㎝
A
D
B
C
E
6.如图,已知△ABC中,AB =3㎝,BC=3.4cm ,AC=4㎝ 且D,E,F分别为AB,BC,AC边的中点,则△DEF的周长是 ㎝.
A
B
C
D
E
F
5.2
7、如下图:在Rt △ ABC中,∠A=90°,D、E、F分别是各边中点, AB=6cm,AC=8cm,则△DEF的周长= cm。
12
⑹
⑺
E
F
B
A
C
D
例2 已知:点O是△ABC内一点,D、E、F、G
分别是AO、BO、CB、CA的中点.
求证:四边形DEFG是平行四边形.
C
A
O
F
G
D
E
D
E
O
变式:如图,在四边形 AOBC中,D、E、F、G、分别是AO、0B、BC、CA的中点,四边形DEFG是什么四边形?为什么?
结论: 顺次连结四边形各边中点所得四边形是平行四边形。
B
GF AB
DE AB
A
B
C
D
E
F
G
H
已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。
证明:连结AC
∵ AE=EB、CF=FB,
(三角形中位线定理)
∴EF∥AC,EF= AC
∴四边形EFGH是平行四边形
同理: HG∥AC,HG= AC
∴EF ∥HG,且EF=HG
证明、求证顺次连结四边形各边中点所得的四边形是平行四边形。
★任意四边形四边中点连线所得的四边形一定是平行四边形。
已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
猜想四边形EFGH的形状并证明.
A
B
C
D
E
F
G
H
变式组:
变式1:若AC=BD, 四边形EFGH是什么图形?
变式2:若AC⊥BD, 四边形EFGH是什么图形?
变式3:若AC=BD,且 AC⊥BD, 四边形EFGH是什么图形?
思考与归纳
1.顺次联结矩形各边中点所得的四边形是 .
A
B
C
D
E
F
G
H
菱形
2.顺次联结等腰梯形各边中点所得的四边形是 .
菱形
A
B
E
C
G
D
H
F
(3)顺次联结 的
四边形的中点得到的四边形是正方形.
归纳:
(1)顺次联结 的
四边形的中点得到的四边形是菱形.
(2)顺次联结 的
四边形的中点得到的四边形是矩形.
对角线相等
对角线垂直
对角线相等且垂直
结 论
原四边形两条对角线
连接四边中点所得四边形
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关.
它的对角线是否垂直
或者是否相等
它的对角线是否垂直
或者是否相等
我思考我快乐
C
A
B
D
F
E
G
H
I
如下图,D、E、F、G、H、I都是各自所在线段的中点,若△GHI的周长是5cm,则△ABC的周长是 cm。
20
知识总结:
1。判定定理:一组对边平行且相等的四边形是平行四边形
2.定义 :连接三角形两边中点的线段叫做三角形的中位线
3.三角形的中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半。
本节课你有哪些收获?
4.顺次连接四边形各边中点所得到的四边形。
5.三角形的中位线定理不仅给出了中位线与第三边的关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.
注意:
在处理问题时,要求同时出现三角形及中位线
①有中点连线而无三角形,要作辅助线产生三角形
②有三角形而无中位线,要连结两边中点得中位线
定 理 应 用:
⑴定理为证明平行关系提供了新的工具
⑵定理为证明一条线段是另一条线段的2倍或 1/2提供了一个新的途径
思考题:已知如图:在△ABC中,AB、BC、CA的中点分别是E、F、G,AD是高。求 证:∠EDG= ∠EFG。
分析:EF是△ABC的中位线
DG是Rt△ADC斜边上的中线
∴EF=DG
你还想到了什么?
苏科版八年级下册 数学
动手操作
给你一个任意的三角形(不要用特殊的三角形如:直角三角形、等腰三角形等),能否只剪一刀,就能将剪开的图形拼成一个平行四边形呢?
A
B
C
D
E
A
D
E
F
1.分别取AB、AC的中点D、E,连接DE;
2.沿DE将△ ABC剪成两部分,并将△ ADE绕点E按顺时针旋转180度,得四边形BCFD.
A
B
C
D
E
F
∵DE=EF 、∠AED=∠CEF 、AE=EC∴△ADE ≌ △CFE
证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∴AD=FC 、∠A=∠ECF
∴AB∥FC
又AD=DB ∴BD∥ CF且 BD =CF
所以 ,四边形BCFD是平行四边形
例1、如图,点D、E分别是△ABC的边AB、AC的中点,求证:四边形BCFD是平行四边形
F
E
思考:
1、一个三角形有几条中位线?
A
B
C
D
例如:DE是△ABC的中位线
三角形的中位线定义:
3条
四个
2、这三条中位线把三角形分成几个三角形?
连结三角形两边中点的线段叫三角形的中位线。
线段:DE、EF、DF
(1)相同之处——都和边的中点有关;
(2)不同之处:
三角形中位线的两个端点都是边的中点;
三角形中线只有一个端点是边的中点,另一端点是三角形的顶点。
C
B
A
E
D
概念对比
C
B
A
D
中线DC
中位线DE
1、如图在等边△ABC中,AD=BD,AE=EC,
B
C
D
E
A
⑴△ADE是什么三角形?
⑶DE与BC有什么样关系?
等边三角形
请思考!
∴DE BC
一般的三角形的中位线与第三边也存在这样的关系吗?
⑵DE是△ABC的什么线?
中位线
又∵DE=EF ∠1=∠2
∴△ADE ≌ △CFE
证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∴AD=FC 、∠A=∠ECF
∴AB∥FC
又AD=DB
∴BD∥ CF且 BD =CF
∴四边形BCFD是平行四边形
还有另外的证法吗?
∴DF∥BC,DF=BC
又∵
即DE∥BC
∵点E是AC的中点∴AE=EC
例1、已知:在△ABC 中,DE是△ABC 的中位线
求证:DE∥BC,且DE= BC 。
A
B
C
D
E
F
1
2
⌒
⌒
A
B
C
E
D
F
证明:如图,延长DE至F,
使EF=DE,连接CD、AF、CF
∵AE=EC DE=EF
∴四边形ADCF是平行四边形
∴AD FC
又∵D为AB中点,
∴DB FC
∴四边形BCFD是平行四边形
∴DF= BC
//
又DE DF
∴DE= BC
∥
C
E
D
F
B
A
证法三:过点C作AB的平行线交DE的延长线于F
∵CF∥AB,
∴∠A=∠ECF
又AE=EC,∠AED=∠CEF
∴△ADE≌△CFE
∴ AD=FC
又DB=AD,∴DB = FC
∥
∴四边形BCFD是平行四边形
∴DE// BC 且DE=EF=1/2BC
三角形中位线定理
三角形的中位线平行于第三边,且等于第三边的一半。
C
A
B
D
E
用符号语言表示
∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.
2
1
(数量关系)
(位置关系)
主要用途:
(1)证明平行
(2)证明一条线段是另一条线段的2倍或
2.如图:在△ABC中,DE是中位线。
(1)若∠ADE=60°,则∠B= ;
(2)若BC=8cm,则DE= cm.
(3)DE +BC=12cm,则BC=
60°
4
8cm
6cm
1.三角形的中位线_______第三边,并且______第三边的_______
平行于
等于
一半
3.若等腰△ABC的周长40cm,AB=AC=14cm,则中位线DE=
E
A
B
C
D
4.如图, MN为△ABC的中位线,若∠ABC=61°则∠AMN= ,若MN=12,则BC= .
A
M
B
C
N
61°
24
5. 如图, △ABC中,D,E分别为AB,AC 的中点,当BC=10㎝时,则DE= .
5㎝
A
D
B
C
E
6.如图,已知△ABC中,AB =3㎝,BC=3.4cm ,AC=4㎝ 且D,E,F分别为AB,BC,AC边的中点,则△DEF的周长是 ㎝.
A
B
C
D
E
F
5.2
7、如下图:在Rt △ ABC中,∠A=90°,D、E、F分别是各边中点, AB=6cm,AC=8cm,则△DEF的周长= cm。
12
⑹
⑺
E
F
B
A
C
D
例2 已知:点O是△ABC内一点,D、E、F、G
分别是AO、BO、CB、CA的中点.
求证:四边形DEFG是平行四边形.
C
A
O
F
G
D
E
D
E
O
变式:如图,在四边形 AOBC中,D、E、F、G、分别是AO、0B、BC、CA的中点,四边形DEFG是什么四边形?为什么?
结论: 顺次连结四边形各边中点所得四边形是平行四边形。
B
GF AB
DE AB
A
B
C
D
E
F
G
H
已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。
证明:连结AC
∵ AE=EB、CF=FB,
(三角形中位线定理)
∴EF∥AC,EF= AC
∴四边形EFGH是平行四边形
同理: HG∥AC,HG= AC
∴EF ∥HG,且EF=HG
证明、求证顺次连结四边形各边中点所得的四边形是平行四边形。
★任意四边形四边中点连线所得的四边形一定是平行四边形。
已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
猜想四边形EFGH的形状并证明.
A
B
C
D
E
F
G
H
变式组:
变式1:若AC=BD, 四边形EFGH是什么图形?
变式2:若AC⊥BD, 四边形EFGH是什么图形?
变式3:若AC=BD,且 AC⊥BD, 四边形EFGH是什么图形?
思考与归纳
1.顺次联结矩形各边中点所得的四边形是 .
A
B
C
D
E
F
G
H
菱形
2.顺次联结等腰梯形各边中点所得的四边形是 .
菱形
A
B
E
C
G
D
H
F
(3)顺次联结 的
四边形的中点得到的四边形是正方形.
归纳:
(1)顺次联结 的
四边形的中点得到的四边形是菱形.
(2)顺次联结 的
四边形的中点得到的四边形是矩形.
对角线相等
对角线垂直
对角线相等且垂直
结 论
原四边形两条对角线
连接四边中点所得四边形
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关.
它的对角线是否垂直
或者是否相等
它的对角线是否垂直
或者是否相等
我思考我快乐
C
A
B
D
F
E
G
H
I
如下图,D、E、F、G、H、I都是各自所在线段的中点,若△GHI的周长是5cm,则△ABC的周长是 cm。
20
知识总结:
1。判定定理:一组对边平行且相等的四边形是平行四边形
2.定义 :连接三角形两边中点的线段叫做三角形的中位线
3.三角形的中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半。
本节课你有哪些收获?
4.顺次连接四边形各边中点所得到的四边形。
5.三角形的中位线定理不仅给出了中位线与第三边的关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.
注意:
在处理问题时,要求同时出现三角形及中位线
①有中点连线而无三角形,要作辅助线产生三角形
②有三角形而无中位线,要连结两边中点得中位线
定 理 应 用:
⑴定理为证明平行关系提供了新的工具
⑵定理为证明一条线段是另一条线段的2倍或 1/2提供了一个新的途径
思考题:已知如图:在△ABC中,AB、BC、CA的中点分别是E、F、G,AD是高。求 证:∠EDG= ∠EFG。
分析:EF是△ABC的中位线
DG是Rt△ADC斜边上的中线
∴EF=DG
你还想到了什么?
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
