苏科版数学七年级下册 7.5多边形的内角和、外角和(共35张PPT)
文档属性
| 名称 | 苏科版数学七年级下册 7.5多边形的内角和、外角和(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 10:27:11 | ||
图片预览





文档简介
7.5 多边形的内角和与外角和
苏教版七年级下册 数学
议一议
小学里我们知道:三角形的三个内角和是1800
(1)在上述过程中,哪些角的大小发生了变化?
如图,在△ABC的边AC所在的直线绕点A按逆时针方向旋转的过程中,直线AC与边BC的延长线分别交于点C1、C2、C3 ……
(2)已知∠BAC=50°、∠ACB=70°,求他们的和, 度量∠BAC1与∠AC1B; ∠BAC2与∠AC2B;∠BAC3与∠AC3B;并分别求它们的和, 你发现了什么?
A
B
C
C
C
1
2
3
C
(1)∠BAC1、∠AC1B、∠BAC2、∠AC2B、∠BAC3、∠AC3B都发生了变化
(2)∠BAC+∠ACB=120°
∠BAC1=65°,∠AC1B= 55° ;∠BAC2=80°, ∠AC2B=40 °;
∠BAC3=90°,∠AC3B= 30°;以上四对角的和均为120 °.
尽管在AC旋转过程中,这些角的度数都在发生变化,但每对角的和均不变.
议一议
小学里我们知道:三角形的三个内角和是
(3)当直线AC 绕点A旋转到AC′,使得AC′∥BC时,度量∠BAC′的度数, 你发现什么?
如图,在△ABC的边AC所在的直线绕点A按逆时针方向旋转的过程中,直线AC与边BC的延长线分别交于点C1、C2、C3 ……
A
B
C
C
C
C
1
2
3
C
当AC′∥BC时,∠BAC=1200
发现:把△ABC的边AC所在的直线绕点A按逆时针方向旋转,直线AC与边BC的延长线分别交于点C1、C2、C3 ……点Cn(n=1,2,3……),在这个过程中,∠BACn的度数逐渐变大,∠ACnB的度数逐渐变小,而∠BACn与∠ACnB的度数之和始终不变,为120 °.当点离点C越来越远时,∠ACnB的度数接近于0,因而当AC′∥BC时,∠C′ACn=∠ACnB,因而∠BAC′的度数为∠BACn与∠ACnB的度数之和.
当AC′∥BC时,∠BAC′+∠B=1800
证一证
理由:∵AC‘∥BC
∴∠CAC‘ =∠C (两直线平行,内错角相等)
∠B+∠BAC‘ =180°(两直线平行,同旁内角互补)
∵∠B+∠BAC‘ =∠B+∠BAC+∠CAC‘=180°
∴∠BAC+∠B+∠C=180°
利用平行同旁内角的180°的方法验证得出三角形的内角和是180°
A
B
C
C’
你能说明这个结论成立的理由吗?
结论:三角形的三个内角和是1800
想一想
三角形的三个内角和是1800
大家还记得小学中用什么办法验证的呢?
剪、拼
A
B
C
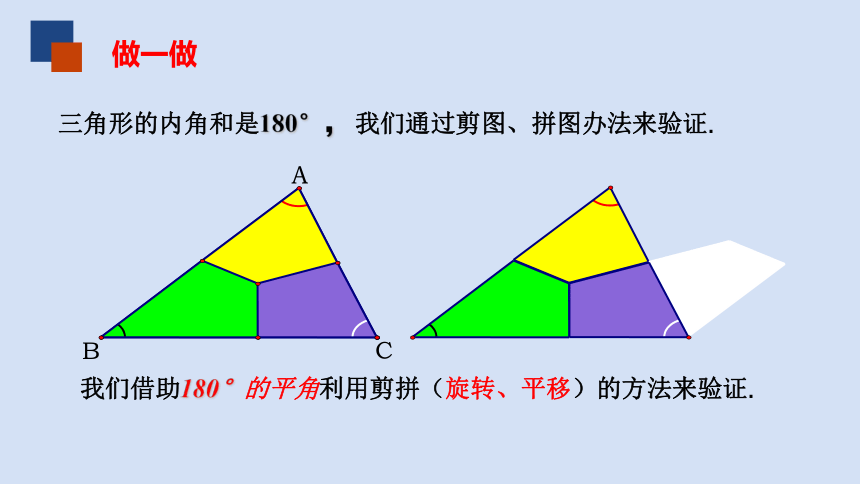
三角形的内角和是180°,我们通过剪图、拼图办法来验证.
做一做
我们借助180°的平角利用剪拼(旋转、平移)的方法来验证.
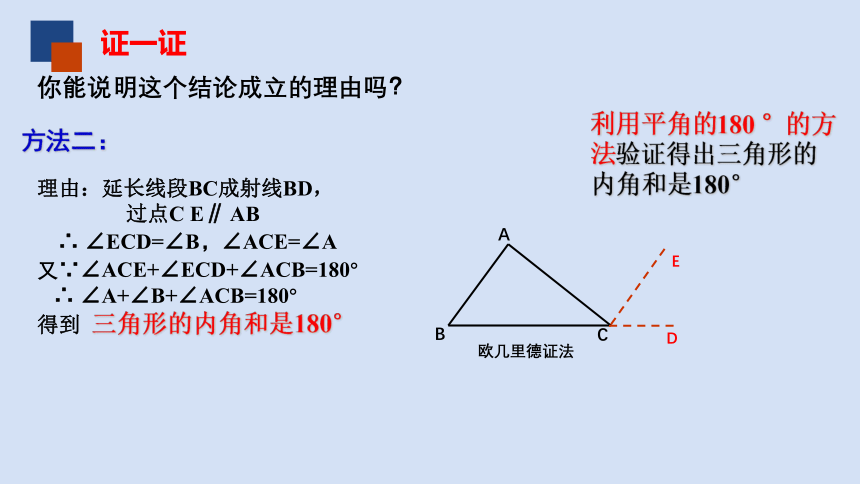
证一证
方法二:
A
B
C
D
E
理由:延长线段BC成射线BD,
过点C E∥ AB
∴ ∠ECD=∠B,∠ACE=∠A
又∵∠ACE+∠ECD+∠ACB=180°
∴ ∠A+∠B+∠ACB=180°
得到 三角形的内角和是180°
利用平角的180 °的方法验证得出三角形的内角和是180°
欧几里德证法
你能说明这个结论成立的理由吗?
2
1
2
2
3
3
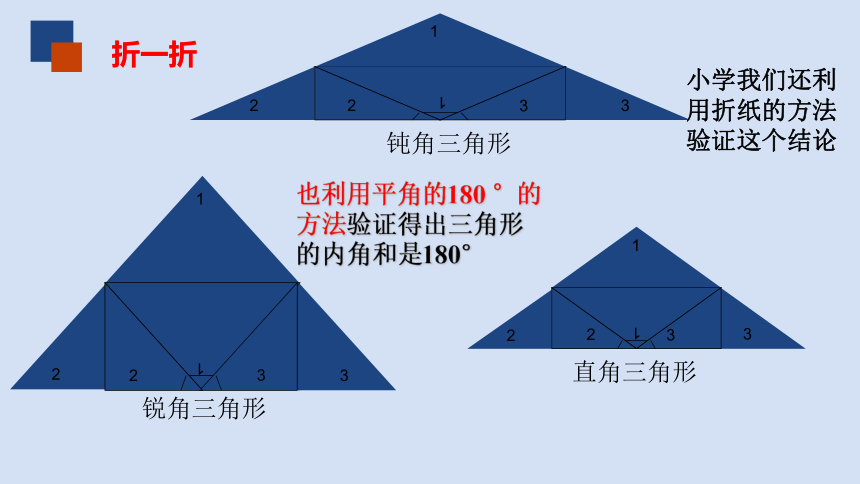
钝角三角形
1
1
1
3
3
锐角三角形
1
1
2
2
3
3
直角三角形
2
折一折
小学我们还利用折纸的方法验证这个结论
也利用平角的180 °的方法验证得出三角形的内角和是180°
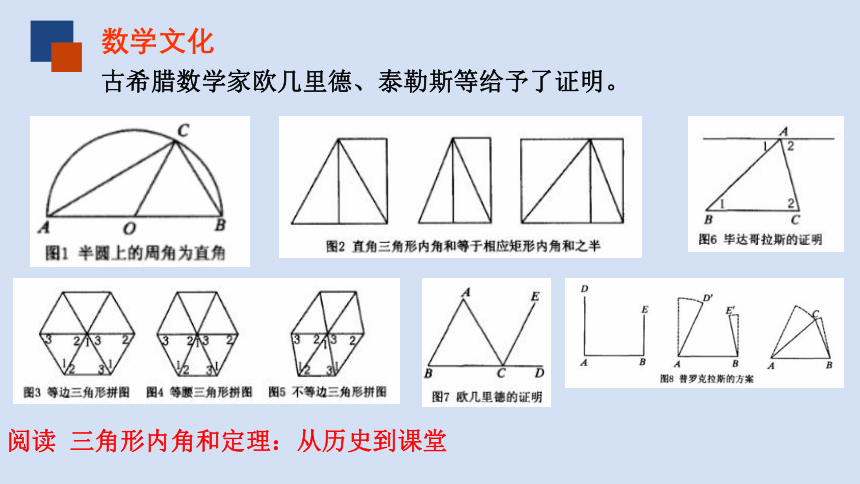
数学文化
帕斯卡(1623—1662),法国数学家、哲学家。早在300多年前也就是这位科学家12 岁时就已经发现这个结论。
有一天他问父亲“什么是几何” ,父亲很简单地回答说“几何就是教人在画图时能作出正确又美观的图”。于是帕斯卡就拿了粉笔在地上画起各种图形来。画着画着,帕斯卡发现任何一个三角形内角和都是180度;又发现三角形三个内角的总和是两个直角。
帕斯卡
数学文化
古希腊数学家欧几里德、泰勒斯等给予了证明。
阅读 三角形内角和定理:从历史到课堂
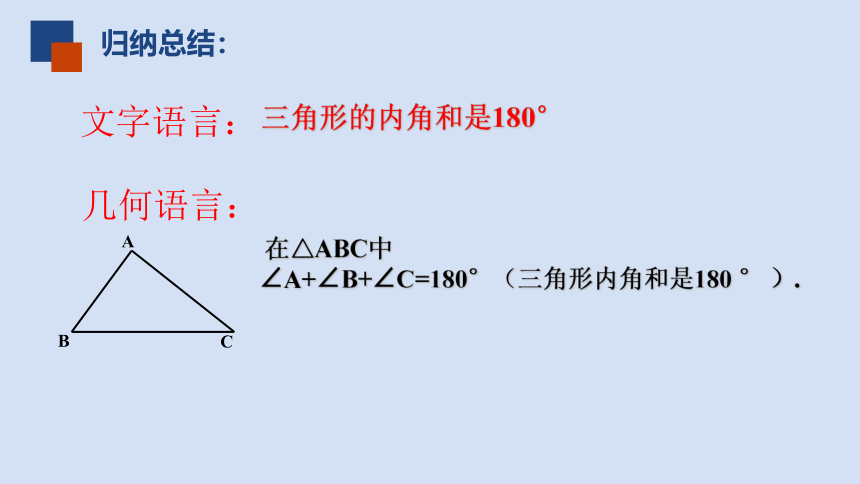
归纳总结:
三角形的内角和是180°
A
B
C
在△ABC中
∠A+∠B+∠C=180°(三角形内角和是180 ° ).
文字语言:
几何语言:
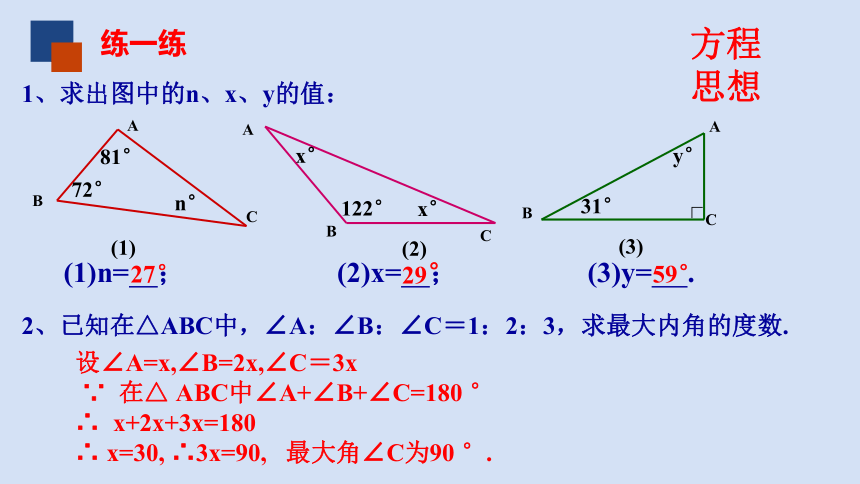
练一练
1、求出图中的n、x、y的值:
81°
72°
n°
(1)
x°
x°
(2)
∟
31°
y°
(3)
122°
27°
29°
59°
A
B
C
A
A
B
B
C
C
(1)n= ; (2)x= ; (3)y= .
2、已知在△ABC中,∠A:∠B:∠C=1:2:3,求最大内角的度数.
方程
思想
设∠A=x,∠B=2x,∠C=3x
∵ 在△ ABC中∠A+∠B+∠C=180 °
∴ x+2x+3x=180
∴ x=30, ∴3x=90, 最大角∠C为90 °.
典型例题
例1 在△ABC中,∠A=40°,∠B=∠C,求∠C的度数.
解:在△ABC中,∠A+∠B+∠C=180°,∠A=40°,得
∠B+∠C=180°-∠A=180°-40°=140°,
∵ ∠B=∠C
∴ ∠C=140°÷2=70°.
典型例题
例2 如图,△ABC的角平分线BD、CE相交于点P, ∠A=70°. 求∠BPC的度数.
1
2
解:在△ABC中, ∠A+∠ABC+ ∠ACB=180 °、 ∠A=70 °得
∠ABC+ ∠ACB=180 °- ∠A=110 °,
∵ BD、CE分别平分∠ABC、∠ACB,
∴ ∠ 1=0.5∠ABC,∠2=0.5∠ACB,
∴ ∠ 1+∠2=0.5(∠ABC+∠ACB)=0.5×110°=55°,
在△PBC中, ∠1+∠2+ ∠BPC=180 °, ∠ 1+∠2=55°,得
∠BPC=180 °-(∠1+∠2)=125°.
整体思想
【思维点拨】求一个角的度数时,常考虑将其放置到三角形内来求值.
作业
2 . △ABC中,若∠A+∠B=∠C,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
1 . 已知在△ABC中,∠A+∠B=2∠C,则∠C= .
3 . 如图1, ∠1+∠2与∠B+∠C有什么数量关系?
4 . 如图2,AC、BD相交于点O, ∠A+∠B与∠C+∠D有什么数量关系?
作业
5 . 如图:在△ABC中,∠ACB=80°,∠1=∠2,求∠BPC的度数。
2
1
P
C
A
B
E
C
B
A
F
D
6 . 如图:CE⊥AF与E,CE与BF交于点D,
∠F=40°,∠C=30°.
求∠EDF,∠DBC的度数.
思考
1、在一个三角形的3个内角中,最多能有几个直角?最多能有几个钝角呢?为什么?
2、如图,在三角形纸片ABC中剪去∠C得到四边形ABDE,且∠1+∠2=230°.求纸片中∠C的度数.
作业答案
1、60°
2、B
3、∠1+∠2=∠B+∠C
这个三角形简称共顶三角形
(或共角三角形、A字形)
4、∠A+∠B=∠C+∠D
这个三角形简称对顶三角形
(或对角三角形、X字形、8字形)
5、解: ∵ ∠ACB=∠1+∠BCP=80°,
又∵ ∠1=∠2 ,
∴ ∠BCP+∠2 =80°,
在△BCP中,∠BCP+∠2+ ∠BPC=180°,得
∠BPC=180°-(∠BCP+∠2)=100°
作业答案
6、解: ∵ CE⊥AF,
∴ ∠FED=90°,
在△DEF中,∠FED+∠F+∠EDF=180°,∠F=40°,得
∠EDF=180°-(∠FED+∠F)=180°-(90°+40°)=50 ° .
由对顶角得∠EDF=∠BDC=50° ,
在△BCD中,∠DBC+∠C+∠BDC=180°,∠C=30°,得
∠DBC=180°-(∠C+∠BDC)=180°-(30°+50°)
=100°.
【思维点拨】求一个角的度数时,常考虑将其放置到三角形内来求值.
找一找
你能从下列图形中找出一些平面图形吗?
认一认
三角形
长方形(矩形)
四边形
我们知道:在平面内,由不在同一条直线上的三条线段,首尾顺次相接组成的图形叫三角形.
类比得到: 在平面内,由不在同一条直线上的3条或3条以上的线段首尾依次相接组成的图形叫做多边形.
六边形
八边形
类比思想
多边形有几条边我们就称几边形,n条边叫n边形
记一记
顶点
内角(角)
边
对角线(连接不相邻两个顶点的线段)
A
B
C
D
E
我们把这个五边形记为:
五边形ABCDE
或五边形AEDCB
友情提醒:表示多边形时字母一定要按时针方向顺序书写
多边形的元素名称
记:对角线BD
不可以记成五边形ACEDB
辩一辩
我们现在研究的是如图1所示的多边形,是凸多边形; 如图2所示的多边形不在我们现在研究的范围中。今后如果不说明,我们讲的多边形都是凸多边形。
凸四边形
你能说出这两个图形的异同点吗?
在多边形中,画任何一边所在直线,其他各边都在这条直线的同一侧
一笔多边形
A
B
C
D
E
探究活动
长方形的内角和是多少?
四边形四个内角和会是多少度呢?
我们知道:三角形的内角和是180 °,那其他多边形的内角和又会是多少呢?
我们不妨从边数最少的多边形开始探究
特殊到一般的方法
猜想:四边形的内角和是360°
探究活动
180°
2
3
4
5
360°=
180 °
×2
n-2
(n-2)×180°
n 边形的内角和=(n-2)·180°
540°=
180 °
×3
720°=
180 °
×4
900°=
180 °
×5
多边形的边数
3
4
5
6
7
…
n
分个数
…
多边形的内角和
…
探索多(n)边形的内角和
利用对角线将多边形分割成若干个三角形,将多边形的内角和转化成多个三角形的内角和
化归思想
对角线是多边形中的常用辅助线
具体到抽象
1
探究活动
多了什么?如何处理?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
此分割方式,将多边形分成(n-1)个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为
(n-1)×180 °- 180 °= (n-2)×180 °
除了利用多边形的对角线分割出若干个三角形外,还可以有其他分割方法吗?
化归思想
探究活动
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
此分割方式,将n边形分割出n个三角形,故所有三角形内角和为n·180 °,但每个图中都有一个以红圈圈住的点处的圆周角360 °不是这个多边形的内角,因此n边形的内角和为
n ·180 °- 360 °= (n-2) ·180 °
多了什么?如何处理?
化归思想
除了上面的两种分割方法分割出多个三角形外,还有吗?
总结归纳
n 边形的内角和=(n-2)·180°
n 边形的内角和是180度的倍数,即多边形的内角和能被180整除。
n 边形的内角和的得出是借助分割化归成多个三角形的内角和计算而成
练一练
1.七边形内角和为 .
2.十边形内角和为 .
3.多边形内角和为1080°,则它是 边形.
900 °=(7-2) ×180 °
1440 °=(10-2) ×180 °
八
(n-2)=1080 °
n=8
方程思想
典型例题
例1 如图,在四边形ABCD中,∠A与∠C互补,∠ABC、∠ADC的平分线分别交CD、AB于点E、F ,∠1与∠2有怎样的数量关系?为什么?
答:∠1与∠2互余
理由:在四边形ABCD中,
∠A+∠ABC+∠C+∠ADC = (4-2) ×180 °=360°
∵ ∠A+∠C = 180 °
∴ ∠ABC+∠ADC = 360°-(∠A+∠C )=180 °
又∵ BE、DF分别平分∠ABC、∠ADC ,得
∴ ∠2=0.5∠ABC,∠1= 0.5∠ADC
∴ ∠1+∠2=0.5(∠ADC +∠ABC)=0.5×180 °=90 °
即∠1与∠2互余.
【思维点拨】求角的度数时,常考虑将其放置到多边形内来求值.
整体思想
典型例题
例2 如图,有一个五角星,你会求∠A+ ∠B+ ∠C+ ∠D+ ∠E的值吗?
A
B
C
D
E
提示:连结CD即可求得。
解:设BD、CE交于点O,
在△BOE、 △COD中
∠B+ ∠E+∠BOE=∠ECD+ ∠BDC+∠COD=180 °
又∠BOE=∠COD
∴∠B+ ∠E=∠ECD+ ∠BDC
在△ACD中,∠A+ ∠ACD+ ∠ADC=180 °
∴ ∠A+ ∠B+ ∠ACE+ ∠ADB+ ∠E=180 °
O
作业
1.已知四边形4个内角的度数比是1︰2︰3︰4,那么这个四边形中最大角的度数是 .
2.一个五边形中有三个内角是直角,其余两个内角都是n°,则n= .
3.六角螺母的面是六边形,它的内角都相等,则这个六边形的每个内角是 .
4. 如图,在三角形纸片ABC中剪去∠C得到四边形ABDE,且∠1+∠2=230°.求纸片中∠C的度数.
1
2
D
C
B
A
E
变式:已知∠C的度数,同学们
可以求哪两个角的和.
作业
5.如图,在五边形ABCDE中, AE∥BC,
求∠C+∠D+∠E的值.
A
B
C
D
E
A
B
C
D
E
F
G
6.如图,则∠A+∠B+∠C+∠D+∠E+∠F+∠G= °.
思考题
1.小明在计算多边形的内角和时,求得其度数是10000,那么小明算的多边形是 边形,内角和是 °.
2.如图:△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部.∠A与∠1+∠2之间存在怎样的数量关系?请试着找出来,并说明理由.
2
1
B
C
D
E
A
思考题
3. 如图:在六边形ABCDEF中,AF∥CD,AB∥DE,且∠BAF=100°,∠BCD=120°,求∠ABC和∠D的度数.
苏教版七年级下册 数学
议一议
小学里我们知道:三角形的三个内角和是1800
(1)在上述过程中,哪些角的大小发生了变化?
如图,在△ABC的边AC所在的直线绕点A按逆时针方向旋转的过程中,直线AC与边BC的延长线分别交于点C1、C2、C3 ……
(2)已知∠BAC=50°、∠ACB=70°,求他们的和, 度量∠BAC1与∠AC1B; ∠BAC2与∠AC2B;∠BAC3与∠AC3B;并分别求它们的和, 你发现了什么?
A
B
C
C
C
1
2
3
C
(1)∠BAC1、∠AC1B、∠BAC2、∠AC2B、∠BAC3、∠AC3B都发生了变化
(2)∠BAC+∠ACB=120°
∠BAC1=65°,∠AC1B= 55° ;∠BAC2=80°, ∠AC2B=40 °;
∠BAC3=90°,∠AC3B= 30°;以上四对角的和均为120 °.
尽管在AC旋转过程中,这些角的度数都在发生变化,但每对角的和均不变.
议一议
小学里我们知道:三角形的三个内角和是
(3)当直线AC 绕点A旋转到AC′,使得AC′∥BC时,度量∠BAC′的度数, 你发现什么?
如图,在△ABC的边AC所在的直线绕点A按逆时针方向旋转的过程中,直线AC与边BC的延长线分别交于点C1、C2、C3 ……
A
B
C
C
C
C
1
2
3
C
当AC′∥BC时,∠BAC=1200
发现:把△ABC的边AC所在的直线绕点A按逆时针方向旋转,直线AC与边BC的延长线分别交于点C1、C2、C3 ……点Cn(n=1,2,3……),在这个过程中,∠BACn的度数逐渐变大,∠ACnB的度数逐渐变小,而∠BACn与∠ACnB的度数之和始终不变,为120 °.当点离点C越来越远时,∠ACnB的度数接近于0,因而当AC′∥BC时,∠C′ACn=∠ACnB,因而∠BAC′的度数为∠BACn与∠ACnB的度数之和.
当AC′∥BC时,∠BAC′+∠B=1800
证一证
理由:∵AC‘∥BC
∴∠CAC‘ =∠C (两直线平行,内错角相等)
∠B+∠BAC‘ =180°(两直线平行,同旁内角互补)
∵∠B+∠BAC‘ =∠B+∠BAC+∠CAC‘=180°
∴∠BAC+∠B+∠C=180°
利用平行同旁内角的180°的方法验证得出三角形的内角和是180°
A
B
C
C’
你能说明这个结论成立的理由吗?
结论:三角形的三个内角和是1800
想一想
三角形的三个内角和是1800
大家还记得小学中用什么办法验证的呢?
剪、拼
A
B
C
三角形的内角和是180°,我们通过剪图、拼图办法来验证.
做一做
我们借助180°的平角利用剪拼(旋转、平移)的方法来验证.
证一证
方法二:
A
B
C
D
E
理由:延长线段BC成射线BD,
过点C E∥ AB
∴ ∠ECD=∠B,∠ACE=∠A
又∵∠ACE+∠ECD+∠ACB=180°
∴ ∠A+∠B+∠ACB=180°
得到 三角形的内角和是180°
利用平角的180 °的方法验证得出三角形的内角和是180°
欧几里德证法
你能说明这个结论成立的理由吗?
2
1
2
2
3
3
钝角三角形
1
1
1
3
3
锐角三角形
1
1
2
2
3
3
直角三角形
2
折一折
小学我们还利用折纸的方法验证这个结论
也利用平角的180 °的方法验证得出三角形的内角和是180°
数学文化
帕斯卡(1623—1662),法国数学家、哲学家。早在300多年前也就是这位科学家12 岁时就已经发现这个结论。
有一天他问父亲“什么是几何” ,父亲很简单地回答说“几何就是教人在画图时能作出正确又美观的图”。于是帕斯卡就拿了粉笔在地上画起各种图形来。画着画着,帕斯卡发现任何一个三角形内角和都是180度;又发现三角形三个内角的总和是两个直角。
帕斯卡
数学文化
古希腊数学家欧几里德、泰勒斯等给予了证明。
阅读 三角形内角和定理:从历史到课堂
归纳总结:
三角形的内角和是180°
A
B
C
在△ABC中
∠A+∠B+∠C=180°(三角形内角和是180 ° ).
文字语言:
几何语言:
练一练
1、求出图中的n、x、y的值:
81°
72°
n°
(1)
x°
x°
(2)
∟
31°
y°
(3)
122°
27°
29°
59°
A
B
C
A
A
B
B
C
C
(1)n= ; (2)x= ; (3)y= .
2、已知在△ABC中,∠A:∠B:∠C=1:2:3,求最大内角的度数.
方程
思想
设∠A=x,∠B=2x,∠C=3x
∵ 在△ ABC中∠A+∠B+∠C=180 °
∴ x+2x+3x=180
∴ x=30, ∴3x=90, 最大角∠C为90 °.
典型例题
例1 在△ABC中,∠A=40°,∠B=∠C,求∠C的度数.
解:在△ABC中,∠A+∠B+∠C=180°,∠A=40°,得
∠B+∠C=180°-∠A=180°-40°=140°,
∵ ∠B=∠C
∴ ∠C=140°÷2=70°.
典型例题
例2 如图,△ABC的角平分线BD、CE相交于点P, ∠A=70°. 求∠BPC的度数.
1
2
解:在△ABC中, ∠A+∠ABC+ ∠ACB=180 °、 ∠A=70 °得
∠ABC+ ∠ACB=180 °- ∠A=110 °,
∵ BD、CE分别平分∠ABC、∠ACB,
∴ ∠ 1=0.5∠ABC,∠2=0.5∠ACB,
∴ ∠ 1+∠2=0.5(∠ABC+∠ACB)=0.5×110°=55°,
在△PBC中, ∠1+∠2+ ∠BPC=180 °, ∠ 1+∠2=55°,得
∠BPC=180 °-(∠1+∠2)=125°.
整体思想
【思维点拨】求一个角的度数时,常考虑将其放置到三角形内来求值.
作业
2 . △ABC中,若∠A+∠B=∠C,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
1 . 已知在△ABC中,∠A+∠B=2∠C,则∠C= .
3 . 如图1, ∠1+∠2与∠B+∠C有什么数量关系?
4 . 如图2,AC、BD相交于点O, ∠A+∠B与∠C+∠D有什么数量关系?
作业
5 . 如图:在△ABC中,∠ACB=80°,∠1=∠2,求∠BPC的度数。
2
1
P
C
A
B
E
C
B
A
F
D
6 . 如图:CE⊥AF与E,CE与BF交于点D,
∠F=40°,∠C=30°.
求∠EDF,∠DBC的度数.
思考
1、在一个三角形的3个内角中,最多能有几个直角?最多能有几个钝角呢?为什么?
2、如图,在三角形纸片ABC中剪去∠C得到四边形ABDE,且∠1+∠2=230°.求纸片中∠C的度数.
作业答案
1、60°
2、B
3、∠1+∠2=∠B+∠C
这个三角形简称共顶三角形
(或共角三角形、A字形)
4、∠A+∠B=∠C+∠D
这个三角形简称对顶三角形
(或对角三角形、X字形、8字形)
5、解: ∵ ∠ACB=∠1+∠BCP=80°,
又∵ ∠1=∠2 ,
∴ ∠BCP+∠2 =80°,
在△BCP中,∠BCP+∠2+ ∠BPC=180°,得
∠BPC=180°-(∠BCP+∠2)=100°
作业答案
6、解: ∵ CE⊥AF,
∴ ∠FED=90°,
在△DEF中,∠FED+∠F+∠EDF=180°,∠F=40°,得
∠EDF=180°-(∠FED+∠F)=180°-(90°+40°)=50 ° .
由对顶角得∠EDF=∠BDC=50° ,
在△BCD中,∠DBC+∠C+∠BDC=180°,∠C=30°,得
∠DBC=180°-(∠C+∠BDC)=180°-(30°+50°)
=100°.
【思维点拨】求一个角的度数时,常考虑将其放置到三角形内来求值.
找一找
你能从下列图形中找出一些平面图形吗?
认一认
三角形
长方形(矩形)
四边形
我们知道:在平面内,由不在同一条直线上的三条线段,首尾顺次相接组成的图形叫三角形.
类比得到: 在平面内,由不在同一条直线上的3条或3条以上的线段首尾依次相接组成的图形叫做多边形.
六边形
八边形
类比思想
多边形有几条边我们就称几边形,n条边叫n边形
记一记
顶点
内角(角)
边
对角线(连接不相邻两个顶点的线段)
A
B
C
D
E
我们把这个五边形记为:
五边形ABCDE
或五边形AEDCB
友情提醒:表示多边形时字母一定要按时针方向顺序书写
多边形的元素名称
记:对角线BD
不可以记成五边形ACEDB
辩一辩
我们现在研究的是如图1所示的多边形,是凸多边形; 如图2所示的多边形不在我们现在研究的范围中。今后如果不说明,我们讲的多边形都是凸多边形。
凸四边形
你能说出这两个图形的异同点吗?
在多边形中,画任何一边所在直线,其他各边都在这条直线的同一侧
一笔多边形
A
B
C
D
E
探究活动
长方形的内角和是多少?
四边形四个内角和会是多少度呢?
我们知道:三角形的内角和是180 °,那其他多边形的内角和又会是多少呢?
我们不妨从边数最少的多边形开始探究
特殊到一般的方法
猜想:四边形的内角和是360°
探究活动
180°
2
3
4
5
360°=
180 °
×2
n-2
(n-2)×180°
n 边形的内角和=(n-2)·180°
540°=
180 °
×3
720°=
180 °
×4
900°=
180 °
×5
多边形的边数
3
4
5
6
7
…
n
分个数
…
多边形的内角和
…
探索多(n)边形的内角和
利用对角线将多边形分割成若干个三角形,将多边形的内角和转化成多个三角形的内角和
化归思想
对角线是多边形中的常用辅助线
具体到抽象
1
探究活动
多了什么?如何处理?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
此分割方式,将多边形分成(n-1)个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为
(n-1)×180 °- 180 °= (n-2)×180 °
除了利用多边形的对角线分割出若干个三角形外,还可以有其他分割方法吗?
化归思想
探究活动
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
此分割方式,将n边形分割出n个三角形,故所有三角形内角和为n·180 °,但每个图中都有一个以红圈圈住的点处的圆周角360 °不是这个多边形的内角,因此n边形的内角和为
n ·180 °- 360 °= (n-2) ·180 °
多了什么?如何处理?
化归思想
除了上面的两种分割方法分割出多个三角形外,还有吗?
总结归纳
n 边形的内角和=(n-2)·180°
n 边形的内角和是180度的倍数,即多边形的内角和能被180整除。
n 边形的内角和的得出是借助分割化归成多个三角形的内角和计算而成
练一练
1.七边形内角和为 .
2.十边形内角和为 .
3.多边形内角和为1080°,则它是 边形.
900 °=(7-2) ×180 °
1440 °=(10-2) ×180 °
八
(n-2)=1080 °
n=8
方程思想
典型例题
例1 如图,在四边形ABCD中,∠A与∠C互补,∠ABC、∠ADC的平分线分别交CD、AB于点E、F ,∠1与∠2有怎样的数量关系?为什么?
答:∠1与∠2互余
理由:在四边形ABCD中,
∠A+∠ABC+∠C+∠ADC = (4-2) ×180 °=360°
∵ ∠A+∠C = 180 °
∴ ∠ABC+∠ADC = 360°-(∠A+∠C )=180 °
又∵ BE、DF分别平分∠ABC、∠ADC ,得
∴ ∠2=0.5∠ABC,∠1= 0.5∠ADC
∴ ∠1+∠2=0.5(∠ADC +∠ABC)=0.5×180 °=90 °
即∠1与∠2互余.
【思维点拨】求角的度数时,常考虑将其放置到多边形内来求值.
整体思想
典型例题
例2 如图,有一个五角星,你会求∠A+ ∠B+ ∠C+ ∠D+ ∠E的值吗?
A
B
C
D
E
提示:连结CD即可求得。
解:设BD、CE交于点O,
在△BOE、 △COD中
∠B+ ∠E+∠BOE=∠ECD+ ∠BDC+∠COD=180 °
又∠BOE=∠COD
∴∠B+ ∠E=∠ECD+ ∠BDC
在△ACD中,∠A+ ∠ACD+ ∠ADC=180 °
∴ ∠A+ ∠B+ ∠ACE+ ∠ADB+ ∠E=180 °
O
作业
1.已知四边形4个内角的度数比是1︰2︰3︰4,那么这个四边形中最大角的度数是 .
2.一个五边形中有三个内角是直角,其余两个内角都是n°,则n= .
3.六角螺母的面是六边形,它的内角都相等,则这个六边形的每个内角是 .
4. 如图,在三角形纸片ABC中剪去∠C得到四边形ABDE,且∠1+∠2=230°.求纸片中∠C的度数.
1
2
D
C
B
A
E
变式:已知∠C的度数,同学们
可以求哪两个角的和.
作业
5.如图,在五边形ABCDE中, AE∥BC,
求∠C+∠D+∠E的值.
A
B
C
D
E
A
B
C
D
E
F
G
6.如图,则∠A+∠B+∠C+∠D+∠E+∠F+∠G= °.
思考题
1.小明在计算多边形的内角和时,求得其度数是10000,那么小明算的多边形是 边形,内角和是 °.
2.如图:△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部.∠A与∠1+∠2之间存在怎样的数量关系?请试着找出来,并说明理由.
2
1
B
C
D
E
A
思考题
3. 如图:在六边形ABCDEF中,AF∥CD,AB∥DE,且∠BAF=100°,∠BCD=120°,求∠ABC和∠D的度数.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
