苏科版数学七年级下册 11.4 解一元一次不等式 课件(共20张PPT)
文档属性
| 名称 | 苏科版数学七年级下册 11.4 解一元一次不等式 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 15:53:53 | ||
图片预览








文档简介
11.4 解一元一次不等式
苏教版七年级下册 数学
1.用不等号表示不等关系的式子叫不等式.
知识回顾:
“>”“<”“≠”“≤”“≥”
3.求不等式的解集的过程,叫做解不等式.
2.一个含有未知数的不等式的所有的解,组成这个
不等式的解的集合,简称这个不等式的解集.
0
-1
x>-1
如果a>b, c>0 , 那么ac>bc (或a ÷ c>b ÷ c)
如果a>b, c<0 , 那么ac < bc (或a ÷ c < b ÷ c)
知识回顾:
如果a>b 那么a+c>b+c(或a-c>b-c)
不等式的基本性质1:
不等式的基本性质2:
知识回顾:
用不等式表示下列数量之间的关系:
(1)小丽每天睡眠时间超过8h,昨天她的睡眠时间是xh;
(2)一辆48座的客车载有x人,途中上来2人后,车内仍有空位;
(3)x的2倍小于x与3的差;
(4)y的3倍与4的和是非负数.
(1)x >8
(2)x+2<48
(3)2x<x-3
(4)3y+4≥0
观察这些不等式:
有哪些共同特点?
新课引入:
只含有一个未知数,并且未知数的次数都是1,系数不等于0.像这样的不等式,叫做一元一次不等式.
(1)x >8
(2)x+2<48
(3)2x<x-3
(4)3y+4≥0
一元一次方程
类比
1.判断下列各式是否是一元一次不等式?
(1)-x≥5;?
(2) y-3x<0;?
(3) 0.5 x+1<0;??
(4) 2≥2x;?
(5) >2.?
是
否
是
是
否
x2+x
典型例题:
(1)2x+y>3;
(2)2x2-3x-2<0;
(3)3x+7>8 ;
(4)x(x+1)>x2 ;
(5)3x+8>x+2(x+2) .
巩固练习:
1.判断下列各式是否是一元一次不等式?
是
否
否
是
否
x>0
8>4
感受新知:
解不等式:2(x+5 ) < 3(x-4)
解:去括号:2x+10 < 3x-12
移项: 2x-3x < -12-10
合并同类项: -x < -22
系数化为1: x>22
解方程: 2(x+5) =3(x-4)
解:去括号: 2x+10=3x-12
移项: 2x-3x=-12-10
合并同类项: -x=-22
系数化为1: x=22
不等号
不等号的
方向改变
类比思想
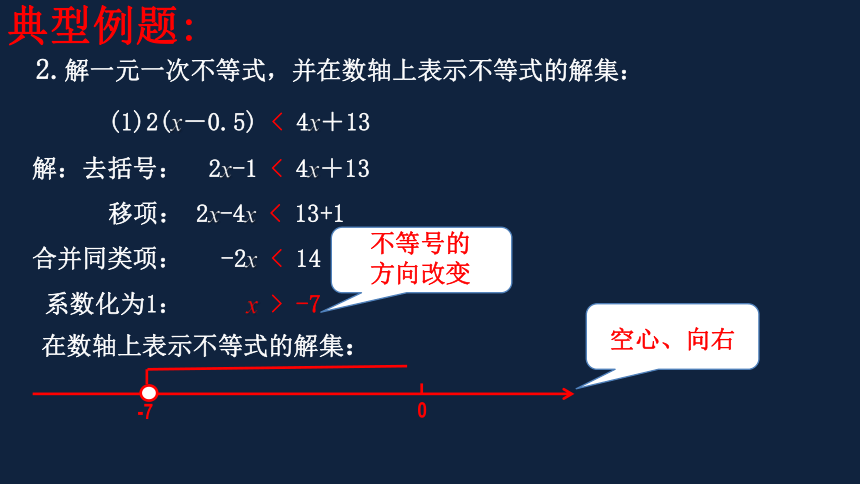
2.解一元一次不等式,并在数轴上表示不等式的解集:
(1)2(x-0.5) < 4x+13
解:去括号: 2x-1 < 4x+13
移项: 2x-4x < 13+1
合并同类项: -2x < 14
系数化为1: x > -7
典型例题:
不等号
不等号的
方向改变
-7
0
不等号
在数轴上表示不等式的解集:
空心、向右
解:10x+6 ≤x-3+6x
10x+6 ≤7x-3
10x-7x ≤-3-6
3x ≤-9
x≤-3
(2) 2(5x+3)≤x-3(1-2x)
典型例题:
0
-3
在数轴上表示不等式的解集:
不等号
不等号的
方向不变
1.去括号;
2.移项;
3.合并同类项;
4.系数化为1.
解一元一次不等式的步骤:
不等号
实心、向左
解一元一次不等式的步骤:
概括总结:
每个步骤
注意事项
不漏乘,括号前面是负号时,里面的各项都要变号;
能合并先合并同类项,移项要变号;
字母不变,系数相加;
不等式两边同除以x系数:正数方向不变,负数方向改变.
1.去括号:
2.移项:
3.合并同类项:
4.系数化为1:
3.当x取何整数值时,代数式2x-4的值大于-3不大于2?
典型例题:
解: -3 < 2x-4 ≤ 2
-3+4 < 2x ≤ 2+6
1 < 2x ≤ 8
0.5 < x ≤ 4
所以,整数x=1,2,3,4.
数形结合
4.已知,3(5x+2)+5<4x-6(x+1),化简|x+1|-|1-x|.
解:15x+6+5<4x-6x-6
15x+11<-2x-6
17x<-17
x<-1
所以,x+1<0
1-x>0
原式=(-x-1)-(1-x)
=-x-1-1+x
=-2
典型例题:
1.已知3m-2x2-m<1是关于x的一元一次不等
式,则m= ,x ______.
巩固练习:
解:2-m=1,m=1,代入不等式,得3-2x<1,
-2x<1-3
x>1
1
>1
不等号
不等号的
方向改变
2.解下列不等式:
(1) 4x ≥ 2x+3 (2)2(x+1)<5x-1
巩固练习:
解: 2x≥3
x ≥1.5
2x+2<5x-1
-3x <-3
x>1
不等号
不等号的
方向改变
(4) 2(x+1)< 4(x+1)- 2
(3)-a-1≤ 2
2.解下列不等式:
(4) 2(x+1)< 4(x+1)- 2
(3)-a-1≤ 2
巩固练习:
-a≤ 3
a≥-3
2 x+2< 4x+4- 2
2x+2< 4x+2
-2x < 0
x > 0
不等号
不等号的
方向改变
不等号
不等号的
方向改变
3.求一元一次不等式10(x+4)+x≤73的非负整数解.
巩固练习:
解: 10x+40+x≤73
11x≤33
x≤3
x的非负整数解是0,1,2,3.
0
2
3
1
数形结合
已知关于x的不等式3x-3<a-ax的解集是x>1,求a的范围.
解:由已知, 3x+ax <a+3
(a+3)x<a+3
因为, x>1
所以, 3+a < 0
a < -3
解
拓展延伸:
变式:解关于x的不等式3x-3<a-ax.
解:由已知, 3x+ax <a+3
(a+3)x<a+3
(1)
即a<-3,
x>1
当a+3<0时,
即a>-3,
x<1
当a+3>0时,
即a=-3,
x无解
(3)当a+3=0时,
分类讨论
(2)
注意:化系数为1,
关注x系数的符号.
拓展延伸:
2.解一元一次不等式的步骤:
课堂小结:
1.一元一次不等式的定义:
只含有一个未知数,并且未知数的次数都是1,
系数不等于0.像这样的不等式,叫做一元一次不等式.
(1)去括号:
(2)移项:
(3)合并同类项:
(4)系数化为1:
不等式两边同除以系数:正数方向不变,负数方向改变.
每个步骤
注意事项
类比思想
分类讨论
苏教版七年级下册 数学
1.用不等号表示不等关系的式子叫不等式.
知识回顾:
“>”“<”“≠”“≤”“≥”
3.求不等式的解集的过程,叫做解不等式.
2.一个含有未知数的不等式的所有的解,组成这个
不等式的解的集合,简称这个不等式的解集.
0
-1
x>-1
如果a>b, c>0 , 那么ac>bc (或a ÷ c>b ÷ c)
如果a>b, c<0 , 那么ac < bc (或a ÷ c < b ÷ c)
知识回顾:
如果a>b 那么a+c>b+c(或a-c>b-c)
不等式的基本性质1:
不等式的基本性质2:
知识回顾:
用不等式表示下列数量之间的关系:
(1)小丽每天睡眠时间超过8h,昨天她的睡眠时间是xh;
(2)一辆48座的客车载有x人,途中上来2人后,车内仍有空位;
(3)x的2倍小于x与3的差;
(4)y的3倍与4的和是非负数.
(1)x >8
(2)x+2<48
(3)2x<x-3
(4)3y+4≥0
观察这些不等式:
有哪些共同特点?
新课引入:
只含有一个未知数,并且未知数的次数都是1,系数不等于0.像这样的不等式,叫做一元一次不等式.
(1)x >8
(2)x+2<48
(3)2x<x-3
(4)3y+4≥0
一元一次方程
类比
1.判断下列各式是否是一元一次不等式?
(1)-x≥5;?
(2) y-3x<0;?
(3) 0.5 x+1<0;??
(4) 2≥2x;?
(5) >2.?
是
否
是
是
否
x2+x
典型例题:
(1)2x+y>3;
(2)2x2-3x-2<0;
(3)3x+7>8 ;
(4)x(x+1)>x2 ;
(5)3x+8>x+2(x+2) .
巩固练习:
1.判断下列各式是否是一元一次不等式?
是
否
否
是
否
x>0
8>4
感受新知:
解不等式:2(x+5 ) < 3(x-4)
解:去括号:2x+10 < 3x-12
移项: 2x-3x < -12-10
合并同类项: -x < -22
系数化为1: x>22
解方程: 2(x+5) =3(x-4)
解:去括号: 2x+10=3x-12
移项: 2x-3x=-12-10
合并同类项: -x=-22
系数化为1: x=22
不等号
不等号的
方向改变
类比思想
2.解一元一次不等式,并在数轴上表示不等式的解集:
(1)2(x-0.5) < 4x+13
解:去括号: 2x-1 < 4x+13
移项: 2x-4x < 13+1
合并同类项: -2x < 14
系数化为1: x > -7
典型例题:
不等号
不等号的
方向改变
-7
0
不等号
在数轴上表示不等式的解集:
空心、向右
解:10x+6 ≤x-3+6x
10x+6 ≤7x-3
10x-7x ≤-3-6
3x ≤-9
x≤-3
(2) 2(5x+3)≤x-3(1-2x)
典型例题:
0
-3
在数轴上表示不等式的解集:
不等号
不等号的
方向不变
1.去括号;
2.移项;
3.合并同类项;
4.系数化为1.
解一元一次不等式的步骤:
不等号
实心、向左
解一元一次不等式的步骤:
概括总结:
每个步骤
注意事项
不漏乘,括号前面是负号时,里面的各项都要变号;
能合并先合并同类项,移项要变号;
字母不变,系数相加;
不等式两边同除以x系数:正数方向不变,负数方向改变.
1.去括号:
2.移项:
3.合并同类项:
4.系数化为1:
3.当x取何整数值时,代数式2x-4的值大于-3不大于2?
典型例题:
解: -3 < 2x-4 ≤ 2
-3+4 < 2x ≤ 2+6
1 < 2x ≤ 8
0.5 < x ≤ 4
所以,整数x=1,2,3,4.
数形结合
4.已知,3(5x+2)+5<4x-6(x+1),化简|x+1|-|1-x|.
解:15x+6+5<4x-6x-6
15x+11<-2x-6
17x<-17
x<-1
所以,x+1<0
1-x>0
原式=(-x-1)-(1-x)
=-x-1-1+x
=-2
典型例题:
1.已知3m-2x2-m<1是关于x的一元一次不等
式,则m= ,x ______.
巩固练习:
解:2-m=1,m=1,代入不等式,得3-2x<1,
-2x<1-3
x>1
1
>1
不等号
不等号的
方向改变
2.解下列不等式:
(1) 4x ≥ 2x+3 (2)2(x+1)<5x-1
巩固练习:
解: 2x≥3
x ≥1.5
2x+2<5x-1
-3x <-3
x>1
不等号
不等号的
方向改变
(4) 2(x+1)< 4(x+1)- 2
(3)-a-1≤ 2
2.解下列不等式:
(4) 2(x+1)< 4(x+1)- 2
(3)-a-1≤ 2
巩固练习:
-a≤ 3
a≥-3
2 x+2< 4x+4- 2
2x+2< 4x+2
-2x < 0
x > 0
不等号
不等号的
方向改变
不等号
不等号的
方向改变
3.求一元一次不等式10(x+4)+x≤73的非负整数解.
巩固练习:
解: 10x+40+x≤73
11x≤33
x≤3
x的非负整数解是0,1,2,3.
0
2
3
1
数形结合
已知关于x的不等式3x-3<a-ax的解集是x>1,求a的范围.
解:由已知, 3x+ax <a+3
(a+3)x<a+3
因为, x>1
所以, 3+a < 0
a < -3
解
拓展延伸:
变式:解关于x的不等式3x-3<a-ax.
解:由已知, 3x+ax <a+3
(a+3)x<a+3
(1)
即a<-3,
x>1
当a+3<0时,
即a>-3,
x<1
当a+3>0时,
即a=-3,
x无解
(3)当a+3=0时,
分类讨论
(2)
注意:化系数为1,
关注x系数的符号.
拓展延伸:
2.解一元一次不等式的步骤:
课堂小结:
1.一元一次不等式的定义:
只含有一个未知数,并且未知数的次数都是1,
系数不等于0.像这样的不等式,叫做一元一次不等式.
(1)去括号:
(2)移项:
(3)合并同类项:
(4)系数化为1:
不等式两边同除以系数:正数方向不变,负数方向改变.
每个步骤
注意事项
类比思想
分类讨论
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
