苏科版数学七年级下册 第九章 整式乘法与因式分解 复习课 课件(共35张PPT)
文档属性
| 名称 | 苏科版数学七年级下册 第九章 整式乘法与因式分解 复习课 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 10:28:52 | ||
图片预览








文档简介
第九章 整式乘法和因式分解 复习课
因式分解
整式乘法
单项式乘单项式
单项式乘多项式
多项式乘多项式
乘法公式
平方差公式
完全平方公式
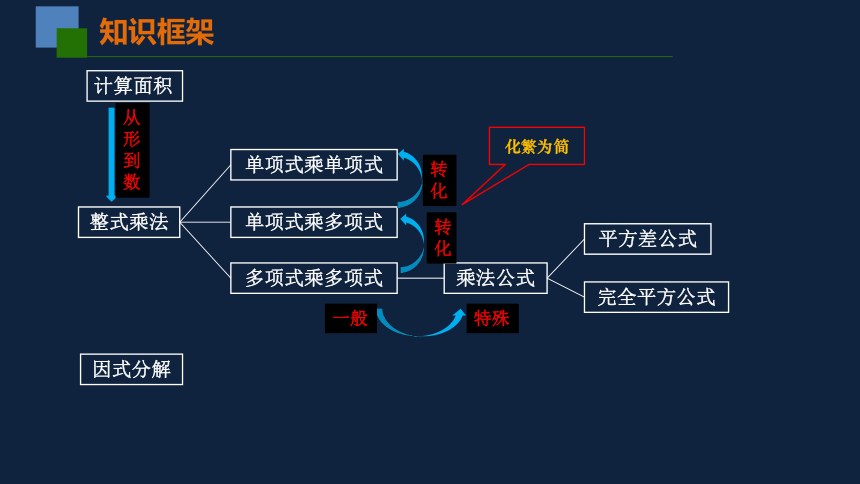
知识框架
转化
转化
计算面积
从形到数
特殊
一般
化繁为简
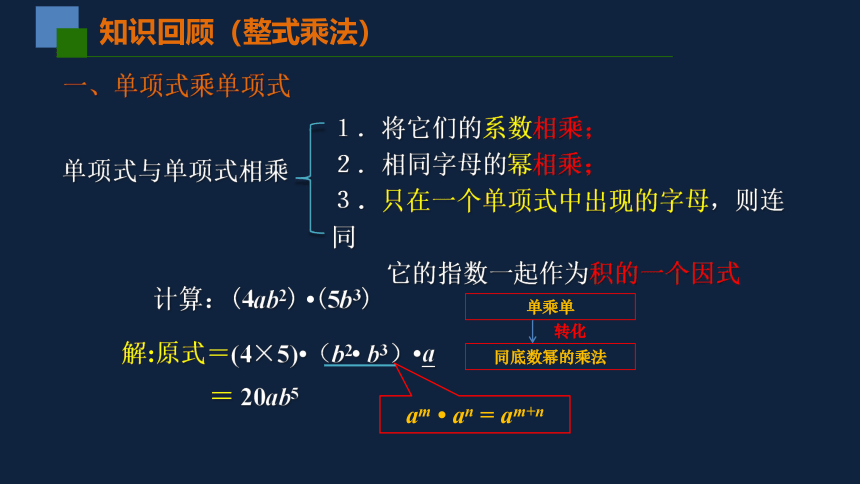
1.将它们的系数相乘;
2.相同字母的幂相乘;
3.只在一个单项式中出现的字母,则连同
它的指数一起作为积的一个因式
知识回顾(整式乘法)
同底数幂的乘法
转化
单乘单
单项式与单项式相乘
一、单项式乘单项式
计算:(4ab2) ?(5b3)
解:原式=(4×5)?(b2? b3)?a
= 20ab5
am ? an = am+n
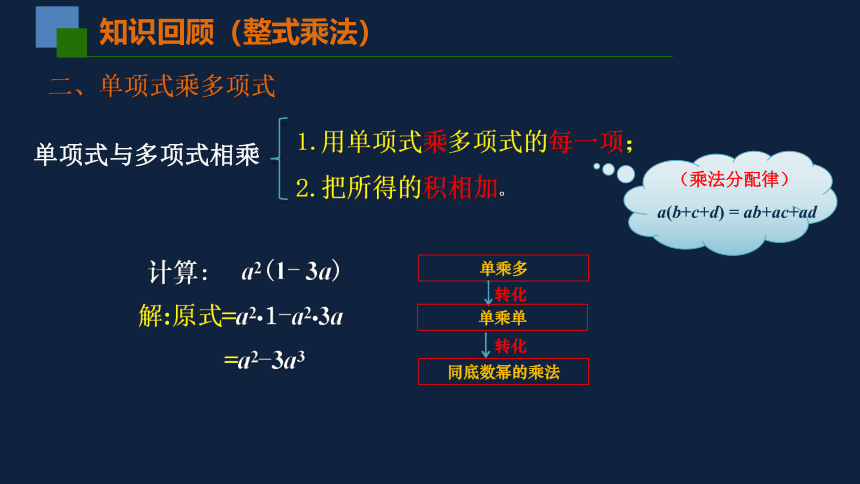
1.用单项式乘多项式的每一项;
2.把所得的积相加。
二、单项式乘多项式
单项式与多项式相乘
(乘法分配律)
a(b+c+d) = ab+ac+ad
计算: a2(1- 3a)
解:原式=a2?1-a2?3a
=a2-3a3
知识回顾(整式乘法)
同底数幂的乘法
转化
单乘多
转化
单乘单
三、多项式乘多项式
1. 用一个多项式的每一项乘另一个多项式
的每一项;
2. 把所得的积相加;
计算:(x+2)(2x-3)
解:原式= x(2x-3)+2(2x-3)
=x?2x+ x?(-3)+2×2x +2×(-3)
=2x2-3x+4x-6
=2x2+x-6
知识回顾(整式乘法)
同底数幂的乘法
转化
单乘单
转化
单乘多
多乘多
转化
合并同类项
多项式与多项式相乘
转化
四、乘法公式
(1)平方差公式: 两个数的和与这两个数的差的积等于这两个数的平方差.
知识回顾(整式乘法)
(a+b) (a-b) =a2-b2
计算:(2x+3)(2x-3)
解:原式= (2x)2-32
= 4x2-9
第一个数为相同数,第二个数为相反数
相同数的平方-相反数的平方
结果为两项
四、乘法公式
(a+b)2=a2+2ab +b2
(a-b)2=a2-2ab+b2
知识回顾(整式乘法)
(2)完全平方公式:两个数的和(或差)的平方等于这两个数平方和加上(或减去)这两个数积的两倍.
计算:(1)(2x+3y) 2
解:原式= (2x)2+2×2x×3y+(3y)2
结果为三项
= 4x2+12xy+ 9y2
(2)(2x-3y) 2
解:原式=(2x)2-2×2x×3y+(3y)2
=4x2-12xy+ 9y2
注意符号要对应
(1) (-b+2a) 2 ( ) (2) (b+2a)(b-2a) ( )
(3) (2a+b)(b+2a) ( ) (4) (2a+b)(2b+a) ( )
(5) (-2a+b)(2a-b) ( ) (6) (-2a+b)(-b-2a) ( )
(7) (-2a+b)(a+2b) ( )
填一填:在下列多项式乘法中,能用完全平方公式计算的请填 A,能用平方差公式计算的请填 B,不能用乘法公式计算的请填 C.
A
B
A
C
知识回顾(整式乘法)
(a+b) (a-b) =a2-b2
(a+b)2=a2 + 2ab + b2
(a-b)2=a2- 2ab + b2
A
B
C
(2a+b) 2
-(2a-b)(2a-b)=- (2a-b) 2
(-2a+b)(-2a-b)
单项式乘单项式
因式分解
乘法公式
整式乘法
单项式乘多项式
多项式乘多项式
平方差公式
完全平方公式
概念
常用方法
步骤
提公因式法
运用公式法
完全平方公式
平方差公式
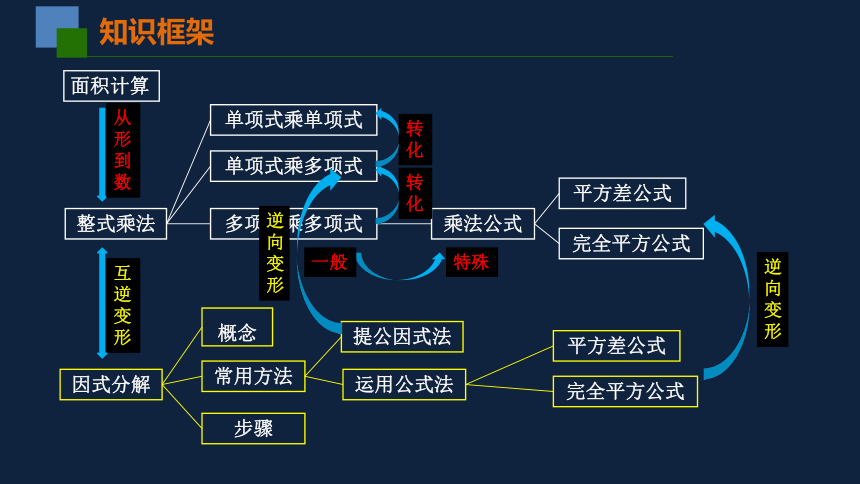
知识框架
转化
转化
逆向变形
互逆变形
面积计算
从形到数
特殊
一般
逆向变形
B.
C.
D.
选择题:下列从左到右的变形中,属于因式分解的是( )
A. (a+3)(a-3)=a2 -9 B.a2-b2=(a+b)(a-b)
C. a2-4a-5=a(a-4)-5 D. a2-4a-5=(a-2) 2-9
知识回顾(因式分解)
1、因式分解概念
把一个多项式写成几个整式的积的形式,叫做多项式的因式分解.
B
知识回顾(因式分解)
2、因式分解的方法
(1)提公因式法:
(逆用乘法分配律)
ab+ac+ad= a(b+c+d)
1.系数取各项系数最大公约数;
2.字母取各项相同的字母;
3.指数取各项最低的.
分解因式:12x2yz - 9x3y
解:原式= 3x2y(4z-3x)
公因式
括号内项数不变
知识回顾(因式分解)
2、因式分解的方法
(2)运用公式法:
把下列各式分解因式:
(1)m2-9n2
解:原式= m2-(3n) 2
a2-b2= (a+b) (a-b)
a2 +2ab+b2= (a+b)2
a2-2ab+b2= (a-b)2
平方差公式:
完全平方公式:
逆用整式乘法公式
(a+b) (a-b) =a2-b2
(a+b)2=a2+2ab + b2
(a-b)2=a2-2ab +b2
=(m+3n)(m-3n)
(2) a2b2 -2ab +1
解:原式= (ab) 2-2ab +12
= (ab-1) 2
第一个数为相同数,第二个数为相反数
两项
三项
注意符号对应
知识回顾(因式分解)
2、因式分解的方法
分解因式:x2+6x+5
解:原式= (x+1) (x+5)
x2+(p+q) x+pq= (x+p) (x+q)
*(3)十字相乘法
1×5
1 + 5
1.二次项系数是1;
3.一次项系数是常数项分解得到的两个因数之和.
2.常数项是两个数之积;
二次三项式
知识回顾(因式分解)
2、因式分解的方法
*(4)分组分解法:
分解因式:x2-y2+ax+ay
解:原式= (x+y)(x-y)+a(x+y)
分组后可以直接提公因式或运用公式进行因式分解(三项以上)
整体
= (x+y)(x-y+a)
1、提取公因式(三步:系数、字母、指数.)
2、用公式(两项用平方差公式;三项用完全平方公式.)
3、查(检查每个因式是否还能继续分解)
知识回顾(因式分解)
3、因式分解的步骤
一提 二用 三查
注意:分解因式必须分解到每一个因式都不能再分解为止
分解因式:3ax4-3ay4
解:原式= 3a(x4-y4)
一提
= 3a(x2+y2) (x+y) (x-y)
三查
二用
= 3a(x2+y2) (x2-y2)
整式乘法(计算):
( 4ab2) ? (5b2)= 20ab3
a2(1- 3a) = a2-3a3
(x+2)(2x-3) =2x2+x-6
(2x+3)(2x-3) = 4x2-9
(2x+3y) 2= 4x2+12xy+ 9y2
知识回顾(整式乘法和因式分解的关系)
因式分解:
12xyz - 9x2 y= 3xy(4z-3x)
m2-9n2=(m+3n)(m- 3n)
a2b2 -2ab +1=(ab-1 ) 2
3ax 4-3ay4 = 3a (x2+y2) (x+y) (x-y) x2-y2+ax+ay= (m+3n)(m- 3n)
积(因式)
和(多项式)
变形
积(因式)
和(多项式)
除单项式乘单项式等于单项式外
变形
例题解析
例1:下列计算中正确的是 ( )
(-4x) ?(2x2-3x-1)=-8x3-12x2-4x
(x+y)(x2+ y2)=x3 + y3
(-4a-1)(4a-1)=1-16a2
(x-2y) 2=x2-2xy+4 y2
C
符号错误
应该为-4xy
展开四项
例题解析
例2:计算
(1) (2x-y)(3x+y)-2x(3x- y)
(2)(a+3)(-3+a)+a(4 –a )
解:原式= (6x2+2xy-3xy-y2)-(6x2-2xy)
= 6x2+2xy-3xy-y2-6x2+2xy
= xy-y2
解:原式= (a2-9)+4a-a2
= a2-9+4a-a2
= 4a-9
多乘多、单乘多
去括号
合并同类项
平方差公式、单乘多
算理
去括号
合并同类项
算理
例题解析
例2:计算
(3)(m+2n)2(m-2n) 2
(4)[( x-y)2+(x+y)2](x2-y2)
(ab)n=anbn
解:原式=[(m+2n)(m-2n)]2
逆用积的乘方公式
=(m2-4n2) 2
平方差公式
=m4-8m2n2+16n4
完全平方公式
解:原式=[(x2-2xy+y2)+(x2+2xy+y2)](x2-y2)
完全平方公式
=(x2-2xy+y2+ x2+2xy+y2) (x2-y2)
去括号
=(2x2+2y2)(x2-y2)
括号内合并同类项
=2(x2+y2)(x2-y2)
提公因式
=2(x4-y4)
平方差公式
也可直接用多项式乘多项式运算
单乘多
=2x4-2y4
结果为和的形式
(单项式或多项式)
算理
算理
例3. 把下列各式分解因式
知识应用(因式分解)
(2) (x-1)(x-3)+1
(1) 4x(a-b)-8y(b-a)
解:原式=x2-3x-x+3+1
多乘多
=x2-4x+4
合并同类项
=(x-2)2
完全平方公式
算理
解:原式=4x (a-b)+8y(a-b)
减法法则
=4(a-b) (x+2y)
提公因式
提公因式要提干净
算理
知识应用(因式分解)
例3. 把下列各式分解因式
(3) x4-2x2+1
解:原式= ( x2-1) 2
完全平方公式
*(4) m2+7m-18
= [( x+1) ( x-1)] 2
平方差公式
= ( x+1)2 ( x-1)2
积的乘方
(ab)n=anbn
解:原式= (m-2) (m+9)
分解因式的结果为积的形式
-2 + 9
-2 × 9
算理
知识梳理
整式乘法和因式分解是既有联系又有区别的两种变形:
整式乘法
ab+ac+ad
a(b+c+d)
整式乘法
a2-b2
(a+b) (a-b)
整式乘法
a2 ± 2ab+b2
(a±b) 2
因式分解
因式分解
因式分解
积
和
类型一:化简求值问题
先化简,再求值: (2x+3)(2x–3)–x(5x+4)–(x–1)2,
其中x2+x–2020=0.
知识应用
解:原式= (4x2–9)–5x2–4x–(x2–2x+1)
= 4x2–9–5x2–4x–x2+2x–1
= –2x2–2x–10
∴原式= –2x2–2x–10
= –2(x2+x)–10
由x2+x–2020=0得: x2+x=2020
如何与已知条件
x2 +x–2020=0产生
联系呢?
平方差公式
单乘多
完全平方公式
= –2×2020–10
= –4050
一个长方形的面积是60cm2,分别以它的长和宽为边长的两个正方形的面积和是136cm2,求长方形的周长.
解:设长方形的长为 a cm,宽为 b cm
则,ab=60, a2+b2=136
而(a+b)2=a2+2ab+b2
因此,a+b=16
∴长方形周长为2(a+b)=32
类型二:实际应用问题
知识应用
=136+120=256
如何求(a+b) 呢?
长×宽=60
长2+宽2=136
结果取正
2.如果|x-y+1|+(x+y -5)2=0,则x2-y2的值是 .
1.若x2 +2ax+36是完全平方式,则a= .
类型三:乘法公式的应用
知识应用
∵ 2a= ±12
∴ a= ±6
±6
∴ x2-y2
=(x+y) (x-y)
= -1×5
= -5
x-y+1=0
x+y-5=0
由题意得:
x-y= -1
x+y= 5
得
-5
类型三:乘法公式的应用
知识应用
3. 已知m、n为有理数,且m2+2m+n2 -6n+10=0,则m= , n= .
原式可化为:m2+2m+1+n2-6n+9=0
-1
3
(m2+2m+1)+(n2-6n+9)=0
(m+1)2+(n-3)2=0
得: m= -1;n=3
分成1和9两个完全平方数
4. 已知 a=2019x+2018,b=2019x+2019, c=2019x+2020 ,则代数式a2+b2+c2-ab-ac-bc的值为( )
A.0 B.1 C.2 D.3
D
类型三:乘法公式的应用
知识应用
由题意得:
a-b=(2019x+2018)-(2019x+2019)= -1
b-c=(2019x+2019)-(2019x+2020)= -1
a-c=(2019x+2018)-(2019x+2020)= -2
a2+a2+b2+b2+c2+c2-2ab-2ac-2bc
2
=
(a2+b2-2ab)+(a2+c2-2ac)+(b2+c2-2bc)
2
=
(a-b)2+(a-c)2+(b-c) 2
2
=
(-1)2+(-2)2+(-1) 2
2
=
1+1+4
2
=
= 3
2(a2+b2+c2-ab-ac-bc)
2
=
原式
(a-b)2+(a-c)2+(b-c) 2
2
=
原式
类型四:整体思想
知识应用
1. 已知 a+b=4,a-b=1,则(a+1)2-(b-1)2的值为 .
原式=[(a+1)+(b-1)] [(a+1)-(b-1)]
=(a+b)(a-b+2)
=4×(1+2)
=12
12
原式=(a2+2a+1)-(b2-2b+1)
=a2+2a+1-b2+2b-1
=a2-b2+2a+2b
=(a+b)(a-b)+2(a+b)
=4×1+2×8
=12
解法(一):先分解因式
解法(二):先用乘法公式展开
整体代入
先用平方差公式分解因式
先用完全平方公式展开
整体代入
(2)另外一名同学发现第四步因式分解的结果不彻底,请你直接写出因式分解
的最后结果 ;
2、请仔细阅读以下内容,然后回答问题:
下面是某同学对多项式 ( x2-4x+2) ( x2-4x+6) +4进行因式分解的过程:
解:令x2-4x+2 =y,则:
原式=y(y+4)+4 (第一步)
= y2+4y+4 (第二步)
= (y+2)2 (第三步)
= (x2-4x+4)2(第四步)
类型四:整体思想
知识应用
C
(x-2)4
(x2-4x+4)2=[(x-2)2]2=(x-2)4.
把括号中的相同部分
(x2-4x+2)看做一个整体
(1)该同学第二步到第三步运用了因式分解的 ;
A.提取公因式 B.平差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
用 x2-4x+2整体替换y
转化为简单的二次三项式
转化后分解因式
整体代入
(3)请你模仿以上方法尝试对多项式( x2-2x) ( x2-2x+2) +1进行因式分解.
类型四:整体思想
知识应用
=(x2-2x+1)2
原式=y(y+2) +1
解:设x2-2x=y.
把x2-2x看做一个整体
=( y+1)2
用 x2-2x整体替换y,并检查能否继续分解
=[( x-1)2]2
= (x-1)4
转化为简单的二次三项式
转化后分解因式
=y2+2y+1
整体代入
类型五:数形结合
知识应用
1. 通过计算几何图形的面积可表示一些代数恒等式,如图可表示的代数恒等式是 .
2a(a+b)=2a2+2ab
如果看成2个正方形和2个长方形的和,
则面积为2a2+2ab.
如果看成一个长方形,则面积为2a(a+b);
类型五:数形结合
知识应用
2. 两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成如下图形,试用不同的方法计算图形的面积,你能发现什么? 请写下来 .
1
2
ab×2+
c2.
1
2
如果看成由3个直角三角形拼合而成,则面积为:
1
2
(a+b) ? ( a+b ) =
(a+b)2 ;
1
2
解:如果看成一个梯形,则面积为:
化简得:a2+b2=c2
1
2
(a+b)2 =
ab×2 +
1
2
1
2
c2
因此有:
a2+b2 =c2
c
c
a
a
b
b
1、计算下列各式,你得到什么结论?试用字母n(n为正整数)表示数说明结论的正确性 .
8×8-7×9;
11×11-10×12;
80×80-79×81.
类型六:探索性问题(归纳思想)
知识应用
=64-63=1
=121-120=1
=6400-6399=1
左边=n2- (n-1)(n+1)
解:结论为n2-(n-1)(n+1)=1
右边=1
∴等式成立
∵左边=右边
前后数字之间有什么联系?
=n2-(n2-1)
=n2-n2+1
=1
2、观察下列式子:
2×4+1=9;
4×6+1=25;
6×8+1=49;
…
探索以上式子的规律,试写出第n个等式,并说明第n个等式成立.
类型六:探索性问题(归纳思想)
知识应用
解:两个连续偶数的积与1的和等于这两个偶数中间奇数的平方
左边:2n( 2n+2)+1 =4n2+4n+1
右边: ( 2n+1)2 =4n2+4n+1
∵左边=右边
∴等式成立
=32
=52
=72
即,第n个等式为:2n( 2n+2)+1=( 2n+1) 2
等式左右的数字有什么联系?
偶数
奇数的平方
偶数+2
课堂小结
1、学习的知识点:灵活运用整式乘法和因式分解的知识
解决相关问题
2、学习的数学思想:整体思想,数形结合,归纳思想
因式分解
整式乘法
单项式乘单项式
单项式乘多项式
多项式乘多项式
乘法公式
平方差公式
完全平方公式
知识框架
转化
转化
计算面积
从形到数
特殊
一般
化繁为简
1.将它们的系数相乘;
2.相同字母的幂相乘;
3.只在一个单项式中出现的字母,则连同
它的指数一起作为积的一个因式
知识回顾(整式乘法)
同底数幂的乘法
转化
单乘单
单项式与单项式相乘
一、单项式乘单项式
计算:(4ab2) ?(5b3)
解:原式=(4×5)?(b2? b3)?a
= 20ab5
am ? an = am+n
1.用单项式乘多项式的每一项;
2.把所得的积相加。
二、单项式乘多项式
单项式与多项式相乘
(乘法分配律)
a(b+c+d) = ab+ac+ad
计算: a2(1- 3a)
解:原式=a2?1-a2?3a
=a2-3a3
知识回顾(整式乘法)
同底数幂的乘法
转化
单乘多
转化
单乘单
三、多项式乘多项式
1. 用一个多项式的每一项乘另一个多项式
的每一项;
2. 把所得的积相加;
计算:(x+2)(2x-3)
解:原式= x(2x-3)+2(2x-3)
=x?2x+ x?(-3)+2×2x +2×(-3)
=2x2-3x+4x-6
=2x2+x-6
知识回顾(整式乘法)
同底数幂的乘法
转化
单乘单
转化
单乘多
多乘多
转化
合并同类项
多项式与多项式相乘
转化
四、乘法公式
(1)平方差公式: 两个数的和与这两个数的差的积等于这两个数的平方差.
知识回顾(整式乘法)
(a+b) (a-b) =a2-b2
计算:(2x+3)(2x-3)
解:原式= (2x)2-32
= 4x2-9
第一个数为相同数,第二个数为相反数
相同数的平方-相反数的平方
结果为两项
四、乘法公式
(a+b)2=a2+2ab +b2
(a-b)2=a2-2ab+b2
知识回顾(整式乘法)
(2)完全平方公式:两个数的和(或差)的平方等于这两个数平方和加上(或减去)这两个数积的两倍.
计算:(1)(2x+3y) 2
解:原式= (2x)2+2×2x×3y+(3y)2
结果为三项
= 4x2+12xy+ 9y2
(2)(2x-3y) 2
解:原式=(2x)2-2×2x×3y+(3y)2
=4x2-12xy+ 9y2
注意符号要对应
(1) (-b+2a) 2 ( ) (2) (b+2a)(b-2a) ( )
(3) (2a+b)(b+2a) ( ) (4) (2a+b)(2b+a) ( )
(5) (-2a+b)(2a-b) ( ) (6) (-2a+b)(-b-2a) ( )
(7) (-2a+b)(a+2b) ( )
填一填:在下列多项式乘法中,能用完全平方公式计算的请填 A,能用平方差公式计算的请填 B,不能用乘法公式计算的请填 C.
A
B
A
C
知识回顾(整式乘法)
(a+b) (a-b) =a2-b2
(a+b)2=a2 + 2ab + b2
(a-b)2=a2- 2ab + b2
A
B
C
(2a+b) 2
-(2a-b)(2a-b)=- (2a-b) 2
(-2a+b)(-2a-b)
单项式乘单项式
因式分解
乘法公式
整式乘法
单项式乘多项式
多项式乘多项式
平方差公式
完全平方公式
概念
常用方法
步骤
提公因式法
运用公式法
完全平方公式
平方差公式
知识框架
转化
转化
逆向变形
互逆变形
面积计算
从形到数
特殊
一般
逆向变形
B.
C.
D.
选择题:下列从左到右的变形中,属于因式分解的是( )
A. (a+3)(a-3)=a2 -9 B.a2-b2=(a+b)(a-b)
C. a2-4a-5=a(a-4)-5 D. a2-4a-5=(a-2) 2-9
知识回顾(因式分解)
1、因式分解概念
把一个多项式写成几个整式的积的形式,叫做多项式的因式分解.
B
知识回顾(因式分解)
2、因式分解的方法
(1)提公因式法:
(逆用乘法分配律)
ab+ac+ad= a(b+c+d)
1.系数取各项系数最大公约数;
2.字母取各项相同的字母;
3.指数取各项最低的.
分解因式:12x2yz - 9x3y
解:原式= 3x2y(4z-3x)
公因式
括号内项数不变
知识回顾(因式分解)
2、因式分解的方法
(2)运用公式法:
把下列各式分解因式:
(1)m2-9n2
解:原式= m2-(3n) 2
a2-b2= (a+b) (a-b)
a2 +2ab+b2= (a+b)2
a2-2ab+b2= (a-b)2
平方差公式:
完全平方公式:
逆用整式乘法公式
(a+b) (a-b) =a2-b2
(a+b)2=a2+2ab + b2
(a-b)2=a2-2ab +b2
=(m+3n)(m-3n)
(2) a2b2 -2ab +1
解:原式= (ab) 2-2ab +12
= (ab-1) 2
第一个数为相同数,第二个数为相反数
两项
三项
注意符号对应
知识回顾(因式分解)
2、因式分解的方法
分解因式:x2+6x+5
解:原式= (x+1) (x+5)
x2+(p+q) x+pq= (x+p) (x+q)
*(3)十字相乘法
1×5
1 + 5
1.二次项系数是1;
3.一次项系数是常数项分解得到的两个因数之和.
2.常数项是两个数之积;
二次三项式
知识回顾(因式分解)
2、因式分解的方法
*(4)分组分解法:
分解因式:x2-y2+ax+ay
解:原式= (x+y)(x-y)+a(x+y)
分组后可以直接提公因式或运用公式进行因式分解(三项以上)
整体
= (x+y)(x-y+a)
1、提取公因式(三步:系数、字母、指数.)
2、用公式(两项用平方差公式;三项用完全平方公式.)
3、查(检查每个因式是否还能继续分解)
知识回顾(因式分解)
3、因式分解的步骤
一提 二用 三查
注意:分解因式必须分解到每一个因式都不能再分解为止
分解因式:3ax4-3ay4
解:原式= 3a(x4-y4)
一提
= 3a(x2+y2) (x+y) (x-y)
三查
二用
= 3a(x2+y2) (x2-y2)
整式乘法(计算):
( 4ab2) ? (5b2)= 20ab3
a2(1- 3a) = a2-3a3
(x+2)(2x-3) =2x2+x-6
(2x+3)(2x-3) = 4x2-9
(2x+3y) 2= 4x2+12xy+ 9y2
知识回顾(整式乘法和因式分解的关系)
因式分解:
12xyz - 9x2 y= 3xy(4z-3x)
m2-9n2=(m+3n)(m- 3n)
a2b2 -2ab +1=(ab-1 ) 2
3ax 4-3ay4 = 3a (x2+y2) (x+y) (x-y) x2-y2+ax+ay= (m+3n)(m- 3n)
积(因式)
和(多项式)
变形
积(因式)
和(多项式)
除单项式乘单项式等于单项式外
变形
例题解析
例1:下列计算中正确的是 ( )
(-4x) ?(2x2-3x-1)=-8x3-12x2-4x
(x+y)(x2+ y2)=x3 + y3
(-4a-1)(4a-1)=1-16a2
(x-2y) 2=x2-2xy+4 y2
C
符号错误
应该为-4xy
展开四项
例题解析
例2:计算
(1) (2x-y)(3x+y)-2x(3x- y)
(2)(a+3)(-3+a)+a(4 –a )
解:原式= (6x2+2xy-3xy-y2)-(6x2-2xy)
= 6x2+2xy-3xy-y2-6x2+2xy
= xy-y2
解:原式= (a2-9)+4a-a2
= a2-9+4a-a2
= 4a-9
多乘多、单乘多
去括号
合并同类项
平方差公式、单乘多
算理
去括号
合并同类项
算理
例题解析
例2:计算
(3)(m+2n)2(m-2n) 2
(4)[( x-y)2+(x+y)2](x2-y2)
(ab)n=anbn
解:原式=[(m+2n)(m-2n)]2
逆用积的乘方公式
=(m2-4n2) 2
平方差公式
=m4-8m2n2+16n4
完全平方公式
解:原式=[(x2-2xy+y2)+(x2+2xy+y2)](x2-y2)
完全平方公式
=(x2-2xy+y2+ x2+2xy+y2) (x2-y2)
去括号
=(2x2+2y2)(x2-y2)
括号内合并同类项
=2(x2+y2)(x2-y2)
提公因式
=2(x4-y4)
平方差公式
也可直接用多项式乘多项式运算
单乘多
=2x4-2y4
结果为和的形式
(单项式或多项式)
算理
算理
例3. 把下列各式分解因式
知识应用(因式分解)
(2) (x-1)(x-3)+1
(1) 4x(a-b)-8y(b-a)
解:原式=x2-3x-x+3+1
多乘多
=x2-4x+4
合并同类项
=(x-2)2
完全平方公式
算理
解:原式=4x (a-b)+8y(a-b)
减法法则
=4(a-b) (x+2y)
提公因式
提公因式要提干净
算理
知识应用(因式分解)
例3. 把下列各式分解因式
(3) x4-2x2+1
解:原式= ( x2-1) 2
完全平方公式
*(4) m2+7m-18
= [( x+1) ( x-1)] 2
平方差公式
= ( x+1)2 ( x-1)2
积的乘方
(ab)n=anbn
解:原式= (m-2) (m+9)
分解因式的结果为积的形式
-2 + 9
-2 × 9
算理
知识梳理
整式乘法和因式分解是既有联系又有区别的两种变形:
整式乘法
ab+ac+ad
a(b+c+d)
整式乘法
a2-b2
(a+b) (a-b)
整式乘法
a2 ± 2ab+b2
(a±b) 2
因式分解
因式分解
因式分解
积
和
类型一:化简求值问题
先化简,再求值: (2x+3)(2x–3)–x(5x+4)–(x–1)2,
其中x2+x–2020=0.
知识应用
解:原式= (4x2–9)–5x2–4x–(x2–2x+1)
= 4x2–9–5x2–4x–x2+2x–1
= –2x2–2x–10
∴原式= –2x2–2x–10
= –2(x2+x)–10
由x2+x–2020=0得: x2+x=2020
如何与已知条件
x2 +x–2020=0产生
联系呢?
平方差公式
单乘多
完全平方公式
= –2×2020–10
= –4050
一个长方形的面积是60cm2,分别以它的长和宽为边长的两个正方形的面积和是136cm2,求长方形的周长.
解:设长方形的长为 a cm,宽为 b cm
则,ab=60, a2+b2=136
而(a+b)2=a2+2ab+b2
因此,a+b=16
∴长方形周长为2(a+b)=32
类型二:实际应用问题
知识应用
=136+120=256
如何求(a+b) 呢?
长×宽=60
长2+宽2=136
结果取正
2.如果|x-y+1|+(x+y -5)2=0,则x2-y2的值是 .
1.若x2 +2ax+36是完全平方式,则a= .
类型三:乘法公式的应用
知识应用
∵ 2a= ±12
∴ a= ±6
±6
∴ x2-y2
=(x+y) (x-y)
= -1×5
= -5
x-y+1=0
x+y-5=0
由题意得:
x-y= -1
x+y= 5
得
-5
类型三:乘法公式的应用
知识应用
3. 已知m、n为有理数,且m2+2m+n2 -6n+10=0,则m= , n= .
原式可化为:m2+2m+1+n2-6n+9=0
-1
3
(m2+2m+1)+(n2-6n+9)=0
(m+1)2+(n-3)2=0
得: m= -1;n=3
分成1和9两个完全平方数
4. 已知 a=2019x+2018,b=2019x+2019, c=2019x+2020 ,则代数式a2+b2+c2-ab-ac-bc的值为( )
A.0 B.1 C.2 D.3
D
类型三:乘法公式的应用
知识应用
由题意得:
a-b=(2019x+2018)-(2019x+2019)= -1
b-c=(2019x+2019)-(2019x+2020)= -1
a-c=(2019x+2018)-(2019x+2020)= -2
a2+a2+b2+b2+c2+c2-2ab-2ac-2bc
2
=
(a2+b2-2ab)+(a2+c2-2ac)+(b2+c2-2bc)
2
=
(a-b)2+(a-c)2+(b-c) 2
2
=
(-1)2+(-2)2+(-1) 2
2
=
1+1+4
2
=
= 3
2(a2+b2+c2-ab-ac-bc)
2
=
原式
(a-b)2+(a-c)2+(b-c) 2
2
=
原式
类型四:整体思想
知识应用
1. 已知 a+b=4,a-b=1,则(a+1)2-(b-1)2的值为 .
原式=[(a+1)+(b-1)] [(a+1)-(b-1)]
=(a+b)(a-b+2)
=4×(1+2)
=12
12
原式=(a2+2a+1)-(b2-2b+1)
=a2+2a+1-b2+2b-1
=a2-b2+2a+2b
=(a+b)(a-b)+2(a+b)
=4×1+2×8
=12
解法(一):先分解因式
解法(二):先用乘法公式展开
整体代入
先用平方差公式分解因式
先用完全平方公式展开
整体代入
(2)另外一名同学发现第四步因式分解的结果不彻底,请你直接写出因式分解
的最后结果 ;
2、请仔细阅读以下内容,然后回答问题:
下面是某同学对多项式 ( x2-4x+2) ( x2-4x+6) +4进行因式分解的过程:
解:令x2-4x+2 =y,则:
原式=y(y+4)+4 (第一步)
= y2+4y+4 (第二步)
= (y+2)2 (第三步)
= (x2-4x+4)2(第四步)
类型四:整体思想
知识应用
C
(x-2)4
(x2-4x+4)2=[(x-2)2]2=(x-2)4.
把括号中的相同部分
(x2-4x+2)看做一个整体
(1)该同学第二步到第三步运用了因式分解的 ;
A.提取公因式 B.平差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
用 x2-4x+2整体替换y
转化为简单的二次三项式
转化后分解因式
整体代入
(3)请你模仿以上方法尝试对多项式( x2-2x) ( x2-2x+2) +1进行因式分解.
类型四:整体思想
知识应用
=(x2-2x+1)2
原式=y(y+2) +1
解:设x2-2x=y.
把x2-2x看做一个整体
=( y+1)2
用 x2-2x整体替换y,并检查能否继续分解
=[( x-1)2]2
= (x-1)4
转化为简单的二次三项式
转化后分解因式
=y2+2y+1
整体代入
类型五:数形结合
知识应用
1. 通过计算几何图形的面积可表示一些代数恒等式,如图可表示的代数恒等式是 .
2a(a+b)=2a2+2ab
如果看成2个正方形和2个长方形的和,
则面积为2a2+2ab.
如果看成一个长方形,则面积为2a(a+b);
类型五:数形结合
知识应用
2. 两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成如下图形,试用不同的方法计算图形的面积,你能发现什么? 请写下来 .
1
2
ab×2+
c2.
1
2
如果看成由3个直角三角形拼合而成,则面积为:
1
2
(a+b) ? ( a+b ) =
(a+b)2 ;
1
2
解:如果看成一个梯形,则面积为:
化简得:a2+b2=c2
1
2
(a+b)2 =
ab×2 +
1
2
1
2
c2
因此有:
a2+b2 =c2
c
c
a
a
b
b
1、计算下列各式,你得到什么结论?试用字母n(n为正整数)表示数说明结论的正确性 .
8×8-7×9;
11×11-10×12;
80×80-79×81.
类型六:探索性问题(归纳思想)
知识应用
=64-63=1
=121-120=1
=6400-6399=1
左边=n2- (n-1)(n+1)
解:结论为n2-(n-1)(n+1)=1
右边=1
∴等式成立
∵左边=右边
前后数字之间有什么联系?
=n2-(n2-1)
=n2-n2+1
=1
2、观察下列式子:
2×4+1=9;
4×6+1=25;
6×8+1=49;
…
探索以上式子的规律,试写出第n个等式,并说明第n个等式成立.
类型六:探索性问题(归纳思想)
知识应用
解:两个连续偶数的积与1的和等于这两个偶数中间奇数的平方
左边:2n( 2n+2)+1 =4n2+4n+1
右边: ( 2n+1)2 =4n2+4n+1
∵左边=右边
∴等式成立
=32
=52
=72
即,第n个等式为:2n( 2n+2)+1=( 2n+1) 2
等式左右的数字有什么联系?
偶数
奇数的平方
偶数+2
课堂小结
1、学习的知识点:灵活运用整式乘法和因式分解的知识
解决相关问题
2、学习的数学思想:整体思想,数形结合,归纳思想
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
