苏科版数学七年级下册7.4认识三角形(共38张PPT)
文档属性
| 名称 | 苏科版数学七年级下册7.4认识三角形(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览






文档简介
7.4认识三角形
苏教版七年级下册 数学
一、情境引入
在这些图案中,有同学们熟悉的平面图形吗?
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
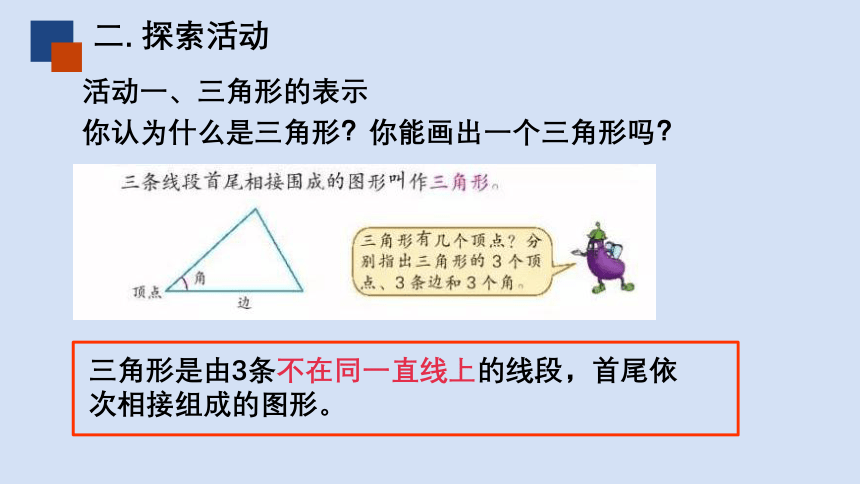
三角形是由3条不在同一直线上的线段,首尾依次相接组成的图形。
二. 探索活动
活动一、三角形的表示
你认为什么是三角形?你能画出一个三角形吗?
a
b
c
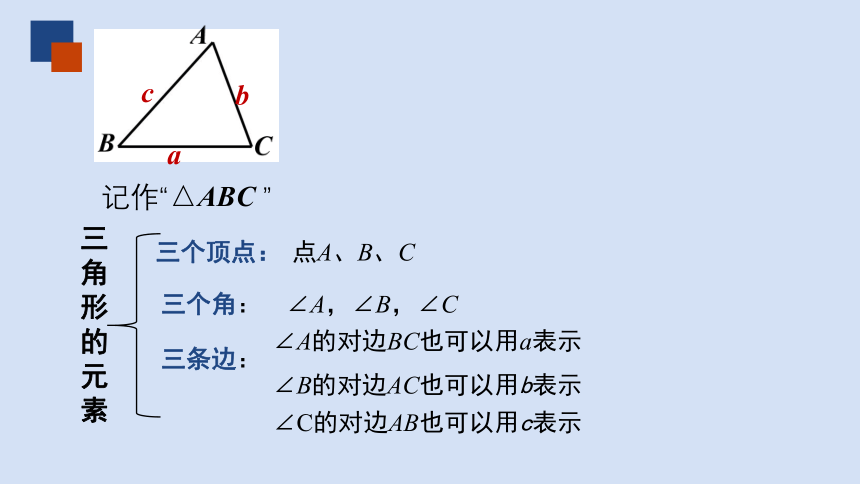
三个顶点:
三个角:
三条边:
三角形的元素
点A、B、C
记作“△ABC ”
∠A,∠B,∠C
∠A的对边BC也可以用a表示
∠B的对边AC也可以用b表示
∠C的对边AB也可以用c表示
三角形的分类
按角的大小分
锐角三角形
直角三角形
钝角三角形
按边长分
不等边三角形
等腰三角形
特别地:等边三角形是特殊的等腰三角形
你能知道你刚才画的三角形是什么三角形吗?你是按照哪种标准判断的?
活动二、三角形的分类
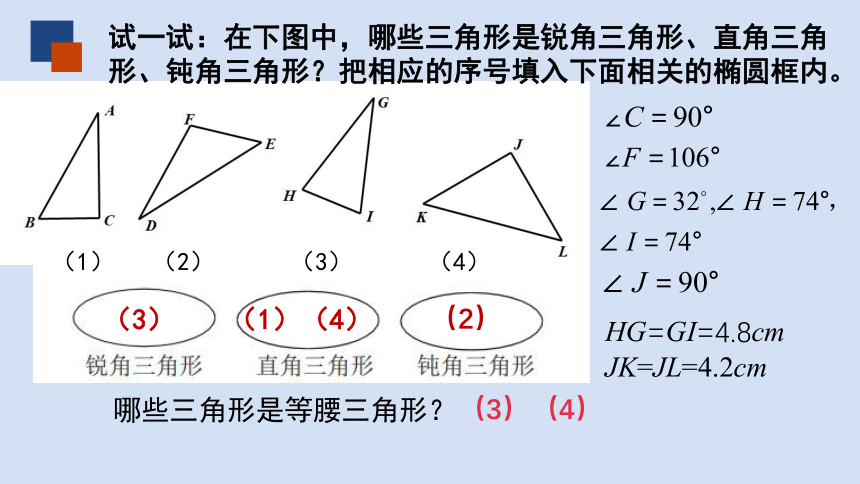
(3)
(1)(4)
(2)
(1) (2) (3) (4)
(3)(4)
哪些三角形是等腰三角形?
试一试:在下图中,哪些三角形是锐角三角形、直角三角形、钝角三角形?把相应的序号填入下面相关的椭圆框内。
HG=GI=4.8cm
JK=JL=4.2cm
练1:写出图中所有三角形,并按角分类。
图中的三角形有:△ACD,△ADE,△EDB,
△ADB,△ACB.
△ADE是锐角三角形
△ACD,△ACB是直角三角形
△EDB,△ADB是钝角三角形
练2.
图中的三角形被木板遮住了一部分,这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上都有可能
D
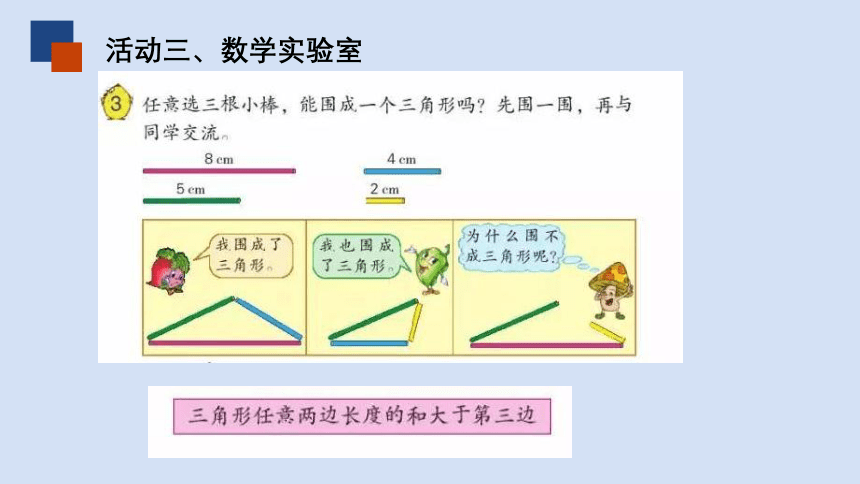
活动三、数学实验室
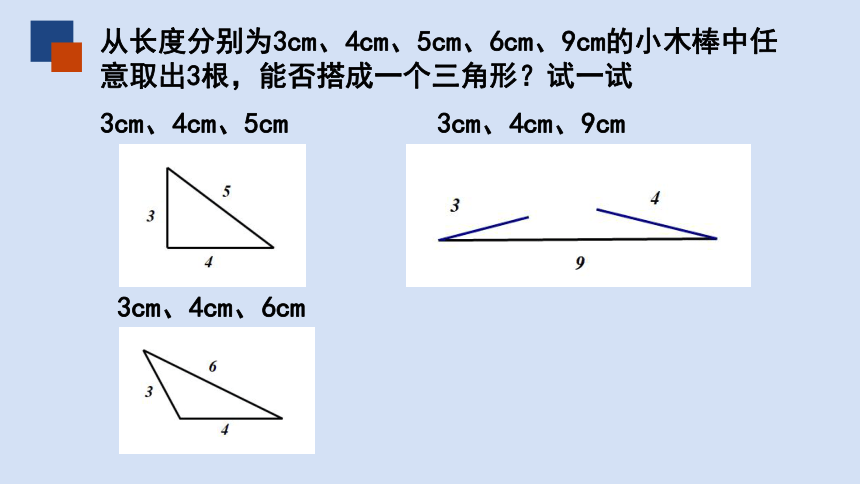
从长度分别为3cm、4cm、5cm、6cm、9cm的小木棒中任意取出3根,能否搭成一个三角形?试一试
3cm、4cm、5cm
3cm、4cm、9cm
3cm、4cm、6cm
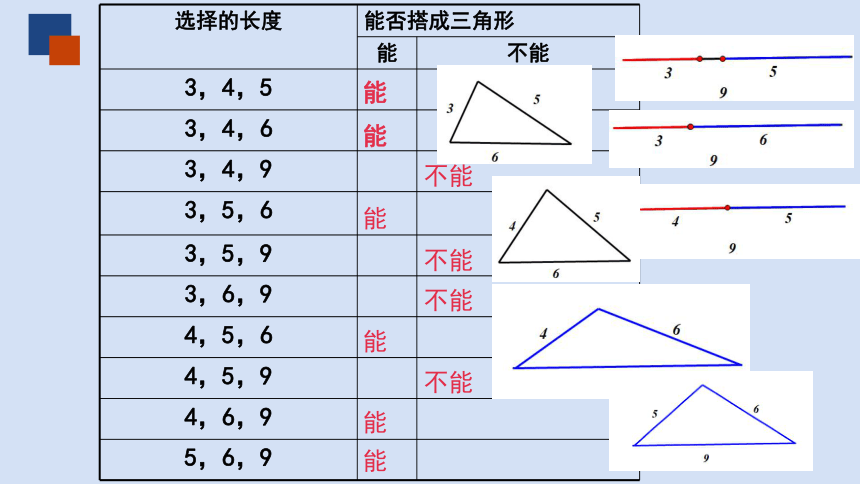
选择的长度
能否搭成三角形
能
不能
3,4,5
3,4,6
3,4,9
3,5,6
3,5,9
3,6,9
4,5,6
4,5,9
4,6,9
5,6,9
能
能
不能
能
不能
不能
能
能
能
不能
3,4,5
3,4,6
3,5,6
4,5,6
4,6,9
5,6,9
3+4>5,3+5>4,4+5>3
3+4>6,3+6>4,4+6>3
3+5>6,3+6>5,5+6>3
4+5>6,4+6>5,5+6>4
4+6>9,4+9>6,6+9>4
5+6>9,5+9>6,6+9>5
3,4,9
3,5,9
3,6,9
4,5,9
3+4<9
3+5<9
3+6=9
4+5=9
通过上面的实验,的确可以猜想得到:
三角形的任意两边之和大于第三边
同理可以得到 AB+BC>AC,
AC+BC>AB。
三角形的任意两边之和大于第三边
猜想
推导
如图,BC是连接B、C两点的线段,
根据基本事实“两点之间线段最短”
可以得AB+AC>BC。
那为什么3cm、4cm、9cm不能搭成三角形呢?
因为3+4<9,只要一组关系不成立就不能构成三角形。
那4cm、5cm、6cm为什么能构成三角形呢?
因为4+5>6,4+6>5,5+6>4。
用较短两边之和与最长边比较就可以。
练3:判断下列长度的3根小木棒能否搭成三角形。
(1)3cm,5cm,10cm ( )
(2)5cm,4cm,9cm ( )
(3)4cm,6cm,9cm ( )
×
×
√
3+5<10
5+4=9
4+6>9
三. 例题选讲
(2)以∠B为内角的三角形有
______________;
△ABC,△ABD,△EBC
(3)在△ABD中,∠BAD的对边为___;
BD
(4)在△AEC中,边EC的对角为___.
∠EAC
(1)图中以AC为边的三角形有
_ ______________;
例1.如图,在△ABC中,点D、E分别在
BC、AB上,AD交CE于点F。
△ABC,△ADC,△AEC,△AFC
例2.
(1)等腰三角形的一边长为4cm,另一边长为5cm,
则周长为_____________;
(2)等腰三角形的一边长为4cm,另一边长为9cm,
则周长为____________.
4,4,5
5,5,4
13cm或14cm
9,9,4
22cm
4,4,9
例3.若a,b,c是△ABC的三边,化简:
因为a+b>c,a+c>b,b+c>a
所以上式=a+b-c+c+a-b+b+c-a
=a+b+c
所以a+b-c>0,b-(c+a)<0,a-(b+c)<0
三角形
符号表示:例如:△ABC,△DEF
元素组成
边:三角形的任意两边之和大于第三边
角:三角形的内角和为180°
分类
按角的大小分:锐角三角形,直角三角形, 钝角三角形
按边长分:不等边三角形,等腰三角形(等边三角形是特殊的等腰三角形)
……
探索新知
橡皮筋的另一端平分BC
.
D
三角形的中线概念:
在三角形中,连接一个顶点与它对边中点
的线段,叫做三角形的中线.
活动一
如图,取△ABC边BC的中点D,连结AD.
如图,线段AD就是△ABC的中线.
D
(2)∵AD为△ABC的中线
∴BD=CD
你能画出这个三角形的所有中线吗?
(1)三角形的中线是一条线段
∵BD=CD
∴AD为△ABC的中线
O
O
O
A
B
C
A2
B2
C2
A1
B1
C1
(3)一个三角形有3条中线
且相交于三角形内部一点。
橡皮筋平分∠BAC
活动二
线段AE叫做△ABC 的角平分线.
E
三角形的角平分线概念:
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
三角形的角平分线与角的平分线一样吗?
画△ABC的∠A的平分线,与边BC
相交于点E.
E
(2)三角形的角平分线平分所在内角;
∵AE为△ABC的角平分线
∴∠BAE=∠EAC
(1)三角形的角平分线是一条线段,而角的平分线是一条射线。
∵ ∠BAE=∠EAC
∴AE为△ABC的角平分线
剪一个三角形纸片,用折纸的方法折出三角形的3条角平分线,你有什么发现?
(3)一个三角形有3条角平分线
且相交于三角形内部一点。
O
O
O
A
B
C
A2
B2
C2
A1
B1
C1
活动三
橡皮筋与BC所在直线垂直
F
三角形的高的概念
在三角形中,从一个顶点向它的对边所在直线作垂线,顶点与垂足之间的线段叫做三角形的高线,简称三角形的高.
如图,线段AF⊥BC,垂足为F,我们把线段AF叫做△ABC的高.
过△ABC的顶点A画边BC所在直线的垂线,且与直线BC相交于点F.
(1)三角形的高也是一条线段;
F
(2)∵AF为△ABC的高
∴AF⊥BC
你能画出这个三角形的所有高吗?
(3)∵AF⊥BC
∴AF为△ABC的高
O
A
B
C
(3)三角形的高线共有3条.
①锐角三角形的3条高交于三角形内一点;
A2
B2
C2
A1
B1
C1
O
O
②直角三角形的3条高交于直角顶点;
③钝角三角形的3条高的所在直线相交于一点。
学以致用
例1 如图,在△ABC中,点D在BC上,且∠BAD=∠CAD,E是AC的中点,BE交AD于点F.指出图中哪条线段是哪个三角形的角平分线,哪条线段是哪个三角形的中线.
解:AD是△ABC的角平分线,
AF是△ABE的角平分线.
BE是△ABC的中线,
DE是△ACD的中线.
例2 如图,在△ABC中,∠C=90°,点D在BC上, DE ⊥AB,垂足为E.指出图中DE、AC分别是哪些三角形的高.
解:DE是△ABD、△AED、△BED的高,
AC是△ACD、△ACB、△ABD的高.
过点A作AE⊥BC,垂足为点E
E
拓展延伸
(1)如图,AD是△ABC的中线。△ABC与△ABD的面积有怎样的数量关系?为什么?
三角形的中线平分三角形的面积
(2)你能把1个三角形分成面积相等的4个三角形吗?试画出相应的图形。
E、D、F是BC的4等分点
AD是△ABC的中线,E是AD的中点
AD是△ABC的中线,E、F分别是AB、AC的中点
AD是△ABC的中线,点E,点F分别是BD、AC的中点
三角形
边:三边关系:三角形的任意两边之和大于第三边
角:三角形的内角和为180°
特殊线段
角平分线
中 线
课堂小结
高
……
谢谢,祝好!
苏教版七年级下册 数学
一、情境引入
在这些图案中,有同学们熟悉的平面图形吗?
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
三角形是由3条不在同一直线上的线段,首尾依次相接组成的图形。
二. 探索活动
活动一、三角形的表示
你认为什么是三角形?你能画出一个三角形吗?
a
b
c
三个顶点:
三个角:
三条边:
三角形的元素
点A、B、C
记作“△ABC ”
∠A,∠B,∠C
∠A的对边BC也可以用a表示
∠B的对边AC也可以用b表示
∠C的对边AB也可以用c表示
三角形的分类
按角的大小分
锐角三角形
直角三角形
钝角三角形
按边长分
不等边三角形
等腰三角形
特别地:等边三角形是特殊的等腰三角形
你能知道你刚才画的三角形是什么三角形吗?你是按照哪种标准判断的?
活动二、三角形的分类
(3)
(1)(4)
(2)
(1) (2) (3) (4)
(3)(4)
哪些三角形是等腰三角形?
试一试:在下图中,哪些三角形是锐角三角形、直角三角形、钝角三角形?把相应的序号填入下面相关的椭圆框内。
HG=GI=4.8cm
JK=JL=4.2cm
练1:写出图中所有三角形,并按角分类。
图中的三角形有:△ACD,△ADE,△EDB,
△ADB,△ACB.
△ADE是锐角三角形
△ACD,△ACB是直角三角形
△EDB,△ADB是钝角三角形
练2.
图中的三角形被木板遮住了一部分,这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上都有可能
D
活动三、数学实验室
从长度分别为3cm、4cm、5cm、6cm、9cm的小木棒中任意取出3根,能否搭成一个三角形?试一试
3cm、4cm、5cm
3cm、4cm、9cm
3cm、4cm、6cm
选择的长度
能否搭成三角形
能
不能
3,4,5
3,4,6
3,4,9
3,5,6
3,5,9
3,6,9
4,5,6
4,5,9
4,6,9
5,6,9
能
能
不能
能
不能
不能
能
能
能
不能
3,4,5
3,4,6
3,5,6
4,5,6
4,6,9
5,6,9
3+4>5,3+5>4,4+5>3
3+4>6,3+6>4,4+6>3
3+5>6,3+6>5,5+6>3
4+5>6,4+6>5,5+6>4
4+6>9,4+9>6,6+9>4
5+6>9,5+9>6,6+9>5
3,4,9
3,5,9
3,6,9
4,5,9
3+4<9
3+5<9
3+6=9
4+5=9
通过上面的实验,的确可以猜想得到:
三角形的任意两边之和大于第三边
同理可以得到 AB+BC>AC,
AC+BC>AB。
三角形的任意两边之和大于第三边
猜想
推导
如图,BC是连接B、C两点的线段,
根据基本事实“两点之间线段最短”
可以得AB+AC>BC。
那为什么3cm、4cm、9cm不能搭成三角形呢?
因为3+4<9,只要一组关系不成立就不能构成三角形。
那4cm、5cm、6cm为什么能构成三角形呢?
因为4+5>6,4+6>5,5+6>4。
用较短两边之和与最长边比较就可以。
练3:判断下列长度的3根小木棒能否搭成三角形。
(1)3cm,5cm,10cm ( )
(2)5cm,4cm,9cm ( )
(3)4cm,6cm,9cm ( )
×
×
√
3+5<10
5+4=9
4+6>9
三. 例题选讲
(2)以∠B为内角的三角形有
______________;
△ABC,△ABD,△EBC
(3)在△ABD中,∠BAD的对边为___;
BD
(4)在△AEC中,边EC的对角为___.
∠EAC
(1)图中以AC为边的三角形有
_ ______________;
例1.如图,在△ABC中,点D、E分别在
BC、AB上,AD交CE于点F。
△ABC,△ADC,△AEC,△AFC
例2.
(1)等腰三角形的一边长为4cm,另一边长为5cm,
则周长为_____________;
(2)等腰三角形的一边长为4cm,另一边长为9cm,
则周长为____________.
4,4,5
5,5,4
13cm或14cm
9,9,4
22cm
4,4,9
例3.若a,b,c是△ABC的三边,化简:
因为a+b>c,a+c>b,b+c>a
所以上式=a+b-c+c+a-b+b+c-a
=a+b+c
所以a+b-c>0,b-(c+a)<0,a-(b+c)<0
三角形
符号表示:例如:△ABC,△DEF
元素组成
边:三角形的任意两边之和大于第三边
角:三角形的内角和为180°
分类
按角的大小分:锐角三角形,直角三角形, 钝角三角形
按边长分:不等边三角形,等腰三角形(等边三角形是特殊的等腰三角形)
……
探索新知
橡皮筋的另一端平分BC
.
D
三角形的中线概念:
在三角形中,连接一个顶点与它对边中点
的线段,叫做三角形的中线.
活动一
如图,取△ABC边BC的中点D,连结AD.
如图,线段AD就是△ABC的中线.
D
(2)∵AD为△ABC的中线
∴BD=CD
你能画出这个三角形的所有中线吗?
(1)三角形的中线是一条线段
∵BD=CD
∴AD为△ABC的中线
O
O
O
A
B
C
A2
B2
C2
A1
B1
C1
(3)一个三角形有3条中线
且相交于三角形内部一点。
橡皮筋平分∠BAC
活动二
线段AE叫做△ABC 的角平分线.
E
三角形的角平分线概念:
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
三角形的角平分线与角的平分线一样吗?
画△ABC的∠A的平分线,与边BC
相交于点E.
E
(2)三角形的角平分线平分所在内角;
∵AE为△ABC的角平分线
∴∠BAE=∠EAC
(1)三角形的角平分线是一条线段,而角的平分线是一条射线。
∵ ∠BAE=∠EAC
∴AE为△ABC的角平分线
剪一个三角形纸片,用折纸的方法折出三角形的3条角平分线,你有什么发现?
(3)一个三角形有3条角平分线
且相交于三角形内部一点。
O
O
O
A
B
C
A2
B2
C2
A1
B1
C1
活动三
橡皮筋与BC所在直线垂直
F
三角形的高的概念
在三角形中,从一个顶点向它的对边所在直线作垂线,顶点与垂足之间的线段叫做三角形的高线,简称三角形的高.
如图,线段AF⊥BC,垂足为F,我们把线段AF叫做△ABC的高.
过△ABC的顶点A画边BC所在直线的垂线,且与直线BC相交于点F.
(1)三角形的高也是一条线段;
F
(2)∵AF为△ABC的高
∴AF⊥BC
你能画出这个三角形的所有高吗?
(3)∵AF⊥BC
∴AF为△ABC的高
O
A
B
C
(3)三角形的高线共有3条.
①锐角三角形的3条高交于三角形内一点;
A2
B2
C2
A1
B1
C1
O
O
②直角三角形的3条高交于直角顶点;
③钝角三角形的3条高的所在直线相交于一点。
学以致用
例1 如图,在△ABC中,点D在BC上,且∠BAD=∠CAD,E是AC的中点,BE交AD于点F.指出图中哪条线段是哪个三角形的角平分线,哪条线段是哪个三角形的中线.
解:AD是△ABC的角平分线,
AF是△ABE的角平分线.
BE是△ABC的中线,
DE是△ACD的中线.
例2 如图,在△ABC中,∠C=90°,点D在BC上, DE ⊥AB,垂足为E.指出图中DE、AC分别是哪些三角形的高.
解:DE是△ABD、△AED、△BED的高,
AC是△ACD、△ACB、△ABD的高.
过点A作AE⊥BC,垂足为点E
E
拓展延伸
(1)如图,AD是△ABC的中线。△ABC与△ABD的面积有怎样的数量关系?为什么?
三角形的中线平分三角形的面积
(2)你能把1个三角形分成面积相等的4个三角形吗?试画出相应的图形。
E、D、F是BC的4等分点
AD是△ABC的中线,E是AD的中点
AD是△ABC的中线,E、F分别是AB、AC的中点
AD是△ABC的中线,点E,点F分别是BD、AC的中点
三角形
边:三边关系:三角形的任意两边之和大于第三边
角:三角形的内角和为180°
特殊线段
角平分线
中 线
课堂小结
高
……
谢谢,祝好!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
