苏科版数学七年级下册7.5《多边形的内角和与外角和》课件(共16张PPT)
文档属性
| 名称 | 苏科版数学七年级下册7.5《多边形的内角和与外角和》课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 435.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览





文档简介
第七章 第5节
苏科版数学七年级下册
探索多边形的内角和与外角和
来看一个问题:
若把一张矩形纸片剪去一角,剩余部分是什么形状的图形 ,它有几条边?
你看我有三条边
你看我有四条边
你看我有五条边
我们都被称为多边形
让我们一起来学习多边形的知识吧!
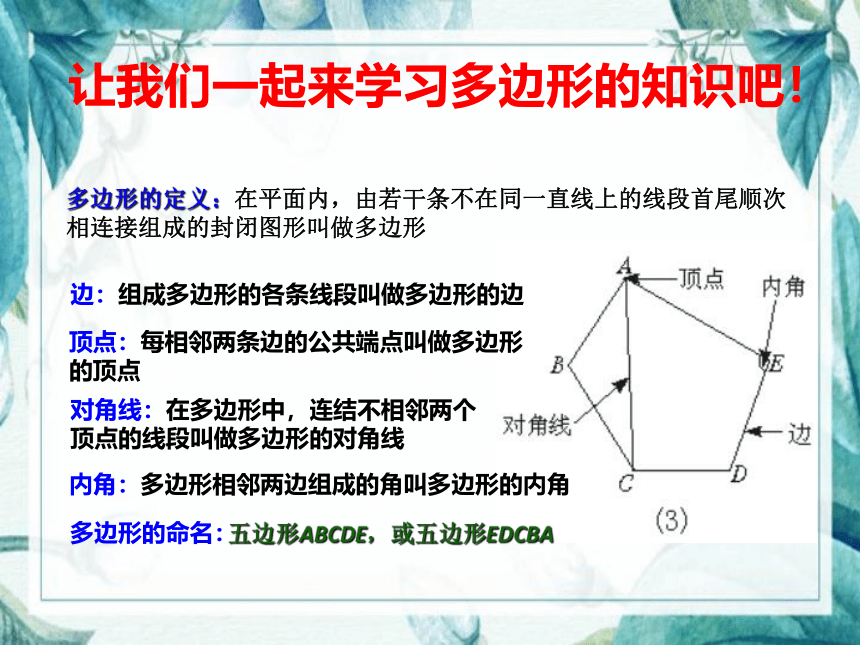
多边形的定义:在平面内,由若干条不在同一直线上的线段首尾顺次相连接组成的封闭图形叫做多边形
边:组成多边形的各条线段叫做多边形的边
顶点:每相邻两条边的公共端点叫做多边形的顶点
对角线:在多边形中,连结不相邻两个顶点的线段叫做多边形的对角线
内角:多边形相邻两边组成的角叫多边形的内角
多边形的命名:
五边形ABCDE,或五边形EDCBA
多边形
的边数
图 形
分割出的三角形的个数
多边形的
内 角 和
3
4
5
------
------
------
------
n
n-2
1
2
3
(3-2)×180?
(4-2)×180?
(5-2)×180?
(n-2)×180?
看谁更聪明:
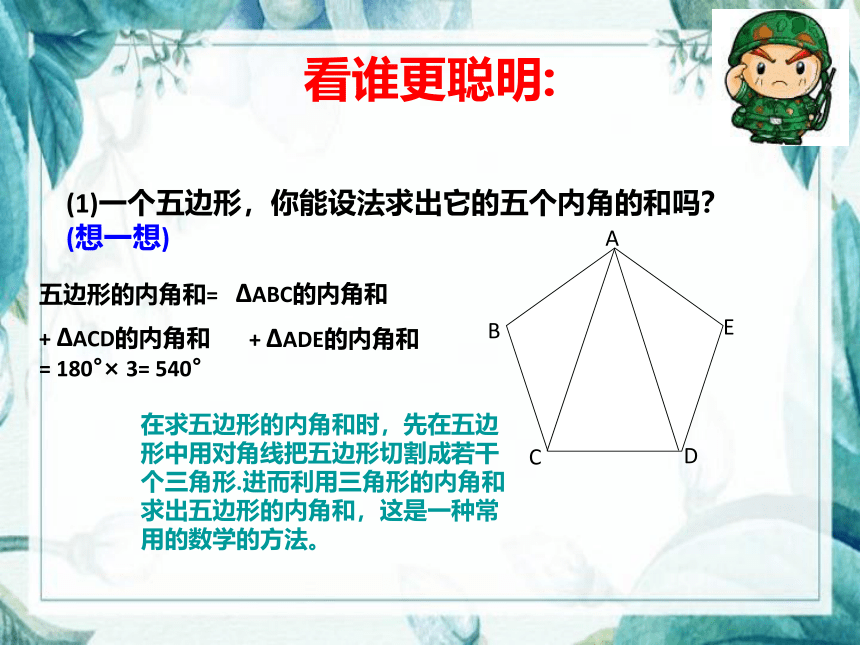
(1)一个五边形,你能设法求出它的五个内角的和吗?(想一想)
在求五边形的内角和时,先在五边形中用对角线把五边形切割成若干个三角形.进而利用三角形的内角和求出五边形的内角和,这是一种常用的数学的方法。
A
E
D
C
B
五边形的内角和=
?ABC的内角和
+ ?ACD的内角和
+ ?ADE的内角和
= 180°× 3= 540°
多边形
三角形
四边形
五边形
六边形
n边形
能分割成几个三角形
内角和
结论:n边形的内角和等于(n-2)·180°
思考一下:
问个问题:12边形的内角和是多少呢?
(12-2)×180°=1800°
2个
3个
4个
(n-2)个
1个
180°×1=180°
180°×2=360°
180°×3=540°
180°×4=720°
180°×
(n-2)
按照上面的办法,你能求出六边形的内角和是多少度吗? 那么n边形的内角和呢?
大家想一想,n边形的内角和公式中,字母n取值有没有范围?
n必须是大于3的整数.
想一想:
n边形的内角和等于(n-2)?180°
(n是整数且n≥3)
你能看出下图中的这些多边形它们的边、角有什么特点吗?
认真观察:
正多边形的定义:
在平面内,内角都相等,边也都相等的多边形叫做正多边形,如右图中的多边形分别为:正三角形、正四边形(即正方形)、正五边形、正六边形、正八边形.
同一图形的内角都相等
同一图形的边都相等
来思考几个问题:
1.一个多边形的边都相等,它的内角一定都相等吗?
2.一个多边形的内角都相等,它的边一定都相等吗?
如菱形的四条边相等,但它的内角不一定都相等,所以应该说:一个多边形的边都相等,它的内角不一定都相等.
如矩形的内角都是直角,但它的边未必都相等,所以应该说:一个多边形的内角都相等,它的边不一定都相等。
3.(1)你能算出正五边形的每个内角的度数吗?
正n边形的每个内角为:
(2)那么正六边形呢?正八边形呢?
(3)你能归纳一下,正多边形的内角度数是怎么算的吗?
108°
120°
135°
能力训练:
1.一个多边形的内角和为2520°,则多边形的边数为_______.
2.多边形得边数增加一条时,其内角和就增加 度
3.下列角度中,不能成为多边形内角和的是( )
A 540° B 280° C 1800° D 900°
5.五边形ABCDE中,若∠A = ∠D = 90°,∠B : ∠C : ∠E = 3:8:7,求∠B ,∠C ,∠E
你学会了吗?
∵(n-2)·180°=2520 °,∴n=16
16
180
B
多边形的内角和必须能被180°整除
4.一个九边形的八个内角都是140°,那么,它的第九个内角为_______度.
140
二、选择题
1、从 n边形的一个顶点出发作对角线,把这个多边形分
成三角形的个数是( )。
A、n B、n-1 C、n-2 D、n-3
2、n边形所有外角的个数是( )。
A、n B、2n C、3n D、不能确定
3、下列说法中,正确的是( )。
A、一个多边形的外角的个数与边数相同;
B、一个多边形的外角的个数是边数的2倍;
C、多边形的外角和是所有外角的和;
D、多边形的外角和是内角和的一半。
4、一个多边形每个外角都是30?,这个多边形是( )。
A、十边形 B、十一边形 C、十二边形 D、十三边形
C
B
B
C
1、已知一个凸多边形的每个内角都等于150度,求
这个多边形的边数。
继续努力:
(1)如图甲,以?ABC的各个顶点为圆心,2cm 为半径画三个圆,则圆与?ABC的公共部分的面积和为_______.
(2)如图乙,以四边形ABCD的各个顶点为圆心,2cm为半径画四个圆,则圆与四边形ABCD的公共部分的面积和为_______.
(3)如图丙,以五边形ABCDE的各个顶点为圆心,2cm为半径画五个圆,则圆与五边形ABCE的公共部分的面积和为_______.
甲
A
B
C
乙
A
C
D
B
丙
B
A
D
C
E
(4)通过(1)、(2)、(3)你能猜想以n边形的各个顶点为圆心,2cm为半径画n个圆,则圆与n边形的公共部分的面积和吗?说说你的理由。
S公共部分=
本节课我们学习了些什么知识?
小结:
1、研究了多边形的定义及其内角和公式,重点探讨了多边形的内角和公式.即:n边形的内角和等于(n-2)·180°,它揭示了多边形内角和与边数之间的关系.
2、正多边形的每个内角为: 它要以知道多边形的内角和为前提
再见
苏科版数学七年级下册
探索多边形的内角和与外角和
来看一个问题:
若把一张矩形纸片剪去一角,剩余部分是什么形状的图形 ,它有几条边?
你看我有三条边
你看我有四条边
你看我有五条边
我们都被称为多边形
让我们一起来学习多边形的知识吧!
多边形的定义:在平面内,由若干条不在同一直线上的线段首尾顺次相连接组成的封闭图形叫做多边形
边:组成多边形的各条线段叫做多边形的边
顶点:每相邻两条边的公共端点叫做多边形的顶点
对角线:在多边形中,连结不相邻两个顶点的线段叫做多边形的对角线
内角:多边形相邻两边组成的角叫多边形的内角
多边形的命名:
五边形ABCDE,或五边形EDCBA
多边形
的边数
图 形
分割出的三角形的个数
多边形的
内 角 和
3
4
5
------
------
------
------
n
n-2
1
2
3
(3-2)×180?
(4-2)×180?
(5-2)×180?
(n-2)×180?
看谁更聪明:
(1)一个五边形,你能设法求出它的五个内角的和吗?(想一想)
在求五边形的内角和时,先在五边形中用对角线把五边形切割成若干个三角形.进而利用三角形的内角和求出五边形的内角和,这是一种常用的数学的方法。
A
E
D
C
B
五边形的内角和=
?ABC的内角和
+ ?ACD的内角和
+ ?ADE的内角和
= 180°× 3= 540°
多边形
三角形
四边形
五边形
六边形
n边形
能分割成几个三角形
内角和
结论:n边形的内角和等于(n-2)·180°
思考一下:
问个问题:12边形的内角和是多少呢?
(12-2)×180°=1800°
2个
3个
4个
(n-2)个
1个
180°×1=180°
180°×2=360°
180°×3=540°
180°×4=720°
180°×
(n-2)
按照上面的办法,你能求出六边形的内角和是多少度吗? 那么n边形的内角和呢?
大家想一想,n边形的内角和公式中,字母n取值有没有范围?
n必须是大于3的整数.
想一想:
n边形的内角和等于(n-2)?180°
(n是整数且n≥3)
你能看出下图中的这些多边形它们的边、角有什么特点吗?
认真观察:
正多边形的定义:
在平面内,内角都相等,边也都相等的多边形叫做正多边形,如右图中的多边形分别为:正三角形、正四边形(即正方形)、正五边形、正六边形、正八边形.
同一图形的内角都相等
同一图形的边都相等
来思考几个问题:
1.一个多边形的边都相等,它的内角一定都相等吗?
2.一个多边形的内角都相等,它的边一定都相等吗?
如菱形的四条边相等,但它的内角不一定都相等,所以应该说:一个多边形的边都相等,它的内角不一定都相等.
如矩形的内角都是直角,但它的边未必都相等,所以应该说:一个多边形的内角都相等,它的边不一定都相等。
3.(1)你能算出正五边形的每个内角的度数吗?
正n边形的每个内角为:
(2)那么正六边形呢?正八边形呢?
(3)你能归纳一下,正多边形的内角度数是怎么算的吗?
108°
120°
135°
能力训练:
1.一个多边形的内角和为2520°,则多边形的边数为_______.
2.多边形得边数增加一条时,其内角和就增加 度
3.下列角度中,不能成为多边形内角和的是( )
A 540° B 280° C 1800° D 900°
5.五边形ABCDE中,若∠A = ∠D = 90°,∠B : ∠C : ∠E = 3:8:7,求∠B ,∠C ,∠E
你学会了吗?
∵(n-2)·180°=2520 °,∴n=16
16
180
B
多边形的内角和必须能被180°整除
4.一个九边形的八个内角都是140°,那么,它的第九个内角为_______度.
140
二、选择题
1、从 n边形的一个顶点出发作对角线,把这个多边形分
成三角形的个数是( )。
A、n B、n-1 C、n-2 D、n-3
2、n边形所有外角的个数是( )。
A、n B、2n C、3n D、不能确定
3、下列说法中,正确的是( )。
A、一个多边形的外角的个数与边数相同;
B、一个多边形的外角的个数是边数的2倍;
C、多边形的外角和是所有外角的和;
D、多边形的外角和是内角和的一半。
4、一个多边形每个外角都是30?,这个多边形是( )。
A、十边形 B、十一边形 C、十二边形 D、十三边形
C
B
B
C
1、已知一个凸多边形的每个内角都等于150度,求
这个多边形的边数。
继续努力:
(1)如图甲,以?ABC的各个顶点为圆心,2cm 为半径画三个圆,则圆与?ABC的公共部分的面积和为_______.
(2)如图乙,以四边形ABCD的各个顶点为圆心,2cm为半径画四个圆,则圆与四边形ABCD的公共部分的面积和为_______.
(3)如图丙,以五边形ABCDE的各个顶点为圆心,2cm为半径画五个圆,则圆与五边形ABCE的公共部分的面积和为_______.
甲
A
B
C
乙
A
C
D
B
丙
B
A
D
C
E
(4)通过(1)、(2)、(3)你能猜想以n边形的各个顶点为圆心,2cm为半径画n个圆,则圆与n边形的公共部分的面积和吗?说说你的理由。
S公共部分=
本节课我们学习了些什么知识?
小结:
1、研究了多边形的定义及其内角和公式,重点探讨了多边形的内角和公式.即:n边形的内角和等于(n-2)·180°,它揭示了多边形内角和与边数之间的关系.
2、正多边形的每个内角为: 它要以知道多边形的内角和为前提
再见
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
