苏科版数学七年级下册7.2平行线性质与判定复习课(共18张PPT)
文档属性
| 名称 | 苏科版数学七年级下册7.2平行线性质与判定复习课(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 09:04:36 | ||
图片预览

文档简介
7.1-7.2平行线性质与判定的复习
苏教版七年级下册 数学
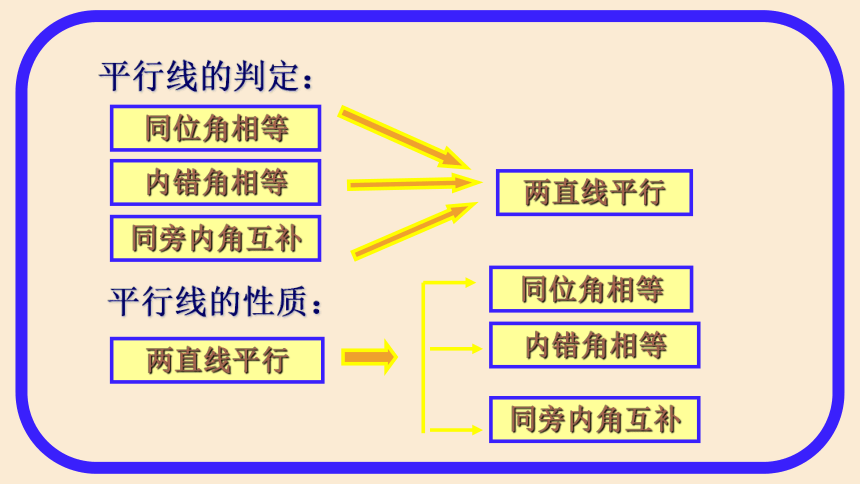
平行线的性质:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定:
两直线平行
同位角相等
内错角相等
同旁内角互补
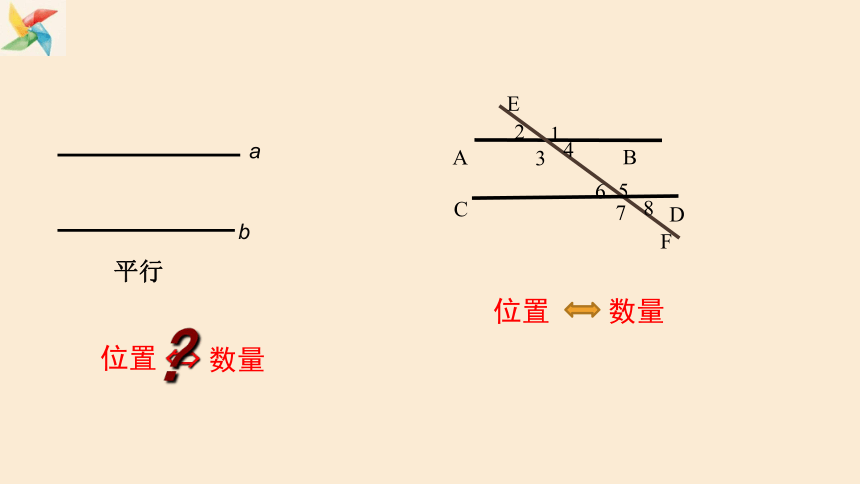
a
b
平行
位置
数量
?
?
A
B
C
D
E
F
1
2
3
4
5
6
7
8
位置
数量
图形
条件
结论
理由
同位角
内错角
同旁内角
a//b
a//b
a//b
同位角相等
两直线平行
内错角相等
两直线平行
同旁内角互补
两直线平行
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
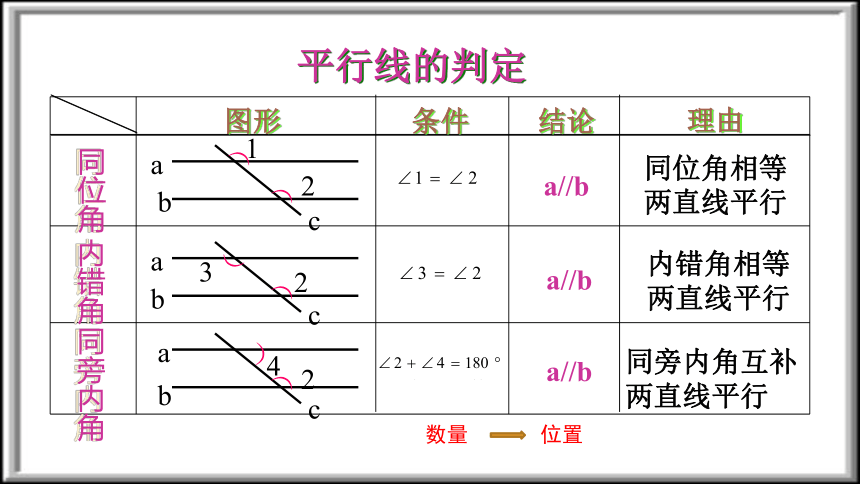
平行线的判定
数量
位置
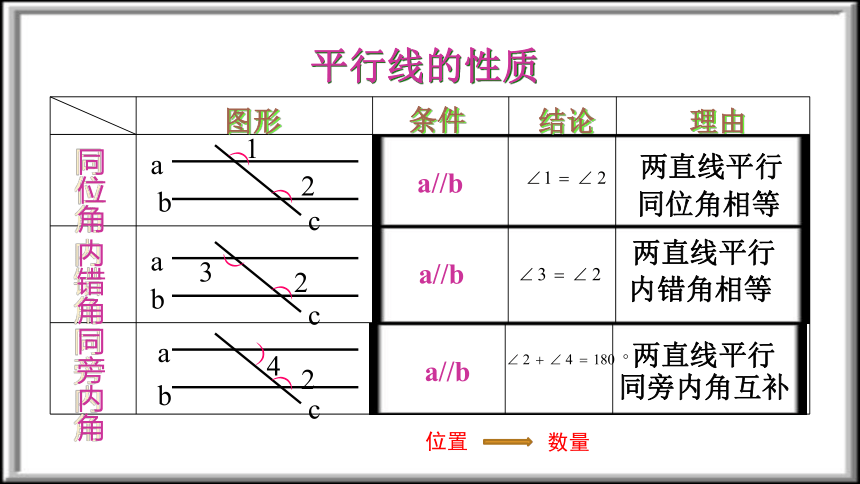
图形
条件
结论
理由
同位角
内错角
同旁内角
a//b
a//b
内错角相等
两直线平行
同旁内角互补
两直线平行
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的性质
a//b
同位角相等
两直线平行
a//b
同位角相等
两直线平行
a//b
同位角相等
两直线平行
a//b
同位角相等
两直线平行
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
位置
数量
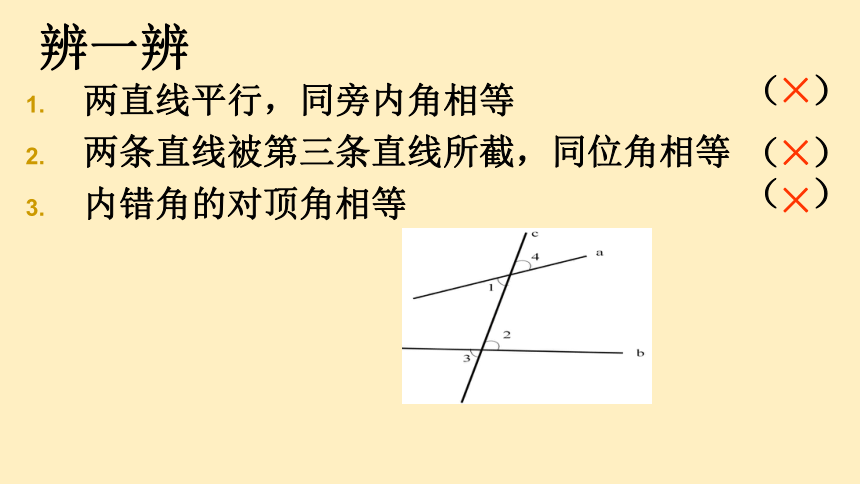
辨一辨
两直线平行,同旁内角相等
两条直线被第三条直线所截,同位角相等
内错角的对顶角相等
( )
( )
( )
×
×
×
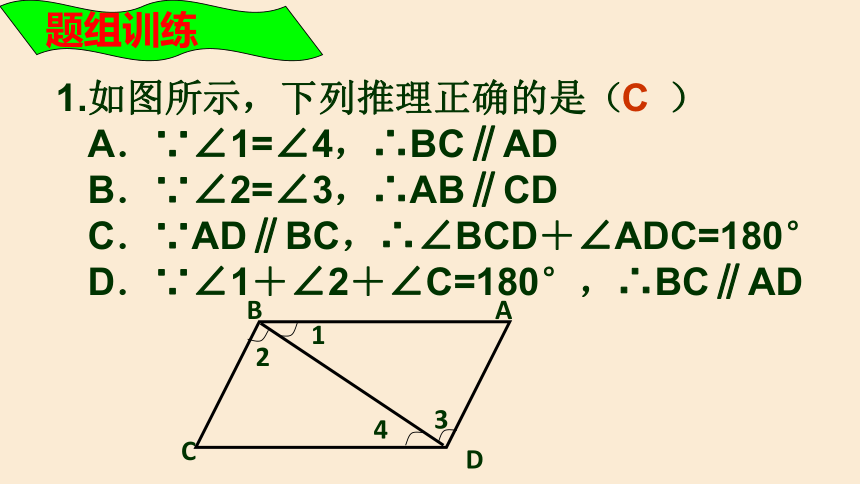
1.如图所示,下列推理正确的是( )
A.∵∠1=∠4,∴BC∥AD
B.∵∠2=∠3,∴AB∥CD
C.∵AD∥BC,∴∠BCD+∠ADC=180°
D.∵∠1+∠2+∠C=180°,∴BC∥AD
2
4
B
C
1
3
A
D
题组训练
C
2.如图,已知AB∥CD,四种说法其中正确的个数是( )
①∠A+∠B=180°;②∠B+∠C=180°;
③∠C+∠D=180°;④∠D+∠A=180°
A.1个 B.2个 C.3个 D.4个
C
D
B
A
B
3、填空:(1) ∵ 2= (已知),
( ).
(2) ∵ AB DF (已知),
2+ =180?( ).
(3) ∵ AC DE (已知),
C= ( ).
(4) ∵ =∠ DFC(已知),
∴ ∥ ( )
∴∠2= ∠ BED ( )
A
C
B
D
E
F
1
2
3
内错角相等,两直线平行
两直线平行,同旁内角互补
两直线平行,同位角相等
DFC
DE AC
AED
1
AB FD
同位角相等,两直线平行
两直线平行,内错角相等
∠A
4.如图:已知: a∥b,
∠1﹕∠2=4 ﹕5,则∠1= 度。
1
2
a
b
c
5.如图:已知:∠1=∠2,则∠C+∠____=____度
6.已知AB ∥ EF ∥ CD, ∠B=400, ∠C=1500,则∠BEC= 度
A
B
E
F
C
D
80
180
10
D
例1 已知:如图:∠1=∠2 , ∠ C=70?,
∠ADE =70°问 BD平分∠ABC吗?
2
1
A
E
D
C
B
∵ ∠ C=70? ,
解:
∴ ∠ADE= ∠C
∴DE∥ BC
又∵∠1= ∠2
∴ ∠1= ∠DBC
∴ BD平分∠ABC
∠ADE= 70?
(已知)
∴∠2=∠DBC
(两直线平行,内错角相等)
(等量代换)
(同位角相等,两直线平行)
(已知)
(等量代换)
(角平分线的定义)
变式(1)已知:如图: BD平分 ABC,
1= 2 , C=70?, 求 ADE 的度数。
2
1
A
E
D
C
B
F
E
D
A
B
C
例3 如图:已知: ∠A=∠D ,∠C=∠F ,
问: CE与BF平行吗?为什么?
1
F
E
D
2
1
A
B
C
变式(2)如图:已知: ∠1=∠2,∠C=∠F
问: ∠A=∠D吗?为什么?
3
4
拓展:
已知:如图:已知: b∥a, c∥a.
求证: b∥c
3
d
c
b
a
2
1
证明: 作直线d,使它与直线a、b、c都相交。
∵ b∥a (已知)
∴∠2=∠1(两直线平行,同位角相等)
∵ c∥a (已知)
∴∠3=∠1(两直线平行,同位角相等)
∴∠2=∠3(等量代换)
∴b∥c(同位角相等,两直线平行)
平行于同一直线的两直线平行
平行线的性质:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行于同一直线的两直线平行
苏教版七年级下册 数学
平行线的性质:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定:
两直线平行
同位角相等
内错角相等
同旁内角互补
a
b
平行
位置
数量
?
?
A
B
C
D
E
F
1
2
3
4
5
6
7
8
位置
数量
图形
条件
结论
理由
同位角
内错角
同旁内角
a//b
a//b
a//b
同位角相等
两直线平行
内错角相等
两直线平行
同旁内角互补
两直线平行
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的判定
数量
位置
图形
条件
结论
理由
同位角
内错角
同旁内角
a//b
a//b
内错角相等
两直线平行
同旁内角互补
两直线平行
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的性质
a//b
同位角相等
两直线平行
a//b
同位角相等
两直线平行
a//b
同位角相等
两直线平行
a//b
同位角相等
两直线平行
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
位置
数量
辨一辨
两直线平行,同旁内角相等
两条直线被第三条直线所截,同位角相等
内错角的对顶角相等
( )
( )
( )
×
×
×
1.如图所示,下列推理正确的是( )
A.∵∠1=∠4,∴BC∥AD
B.∵∠2=∠3,∴AB∥CD
C.∵AD∥BC,∴∠BCD+∠ADC=180°
D.∵∠1+∠2+∠C=180°,∴BC∥AD
2
4
B
C
1
3
A
D
题组训练
C
2.如图,已知AB∥CD,四种说法其中正确的个数是( )
①∠A+∠B=180°;②∠B+∠C=180°;
③∠C+∠D=180°;④∠D+∠A=180°
A.1个 B.2个 C.3个 D.4个
C
D
B
A
B
3、填空:(1) ∵ 2= (已知),
( ).
(2) ∵ AB DF (已知),
2+ =180?( ).
(3) ∵ AC DE (已知),
C= ( ).
(4) ∵ =∠ DFC(已知),
∴ ∥ ( )
∴∠2= ∠ BED ( )
A
C
B
D
E
F
1
2
3
内错角相等,两直线平行
两直线平行,同旁内角互补
两直线平行,同位角相等
DFC
DE AC
AED
1
AB FD
同位角相等,两直线平行
两直线平行,内错角相等
∠A
4.如图:已知: a∥b,
∠1﹕∠2=4 ﹕5,则∠1= 度。
1
2
a
b
c
5.如图:已知:∠1=∠2,则∠C+∠____=____度
6.已知AB ∥ EF ∥ CD, ∠B=400, ∠C=1500,则∠BEC= 度
A
B
E
F
C
D
80
180
10
D
例1 已知:如图:∠1=∠2 , ∠ C=70?,
∠ADE =70°问 BD平分∠ABC吗?
2
1
A
E
D
C
B
∵ ∠ C=70? ,
解:
∴ ∠ADE= ∠C
∴DE∥ BC
又∵∠1= ∠2
∴ ∠1= ∠DBC
∴ BD平分∠ABC
∠ADE= 70?
(已知)
∴∠2=∠DBC
(两直线平行,内错角相等)
(等量代换)
(同位角相等,两直线平行)
(已知)
(等量代换)
(角平分线的定义)
变式(1)已知:如图: BD平分 ABC,
1= 2 , C=70?, 求 ADE 的度数。
2
1
A
E
D
C
B
F
E
D
A
B
C
例3 如图:已知: ∠A=∠D ,∠C=∠F ,
问: CE与BF平行吗?为什么?
1
F
E
D
2
1
A
B
C
变式(2)如图:已知: ∠1=∠2,∠C=∠F
问: ∠A=∠D吗?为什么?
3
4
拓展:
已知:如图:已知: b∥a, c∥a.
求证: b∥c
3
d
c
b
a
2
1
证明: 作直线d,使它与直线a、b、c都相交。
∵ b∥a (已知)
∴∠2=∠1(两直线平行,同位角相等)
∵ c∥a (已知)
∴∠3=∠1(两直线平行,同位角相等)
∴∠2=∠3(等量代换)
∴b∥c(同位角相等,两直线平行)
平行于同一直线的两直线平行
平行线的性质:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行于同一直线的两直线平行
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
