苏科版数学七年级下册专题复习:7.2平行线的判定与性质课件(32张PPT)
文档属性
| 名称 | 苏科版数学七年级下册专题复习:7.2平行线的判定与性质课件(32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 10:43:33 | ||
图片预览







文档简介
专题复行线的判定与性质
苏科版七年级下册
数学
几何学的光荣,在于它从很少几条独立
自主的原则出发,而得以完成如此多的
工作。
----牛顿
1、掌握平行线的性质,能运用平行线的判定与性质进行角的计算与证明;
2、在问题探究中,仔细观察、比较、联想、分析、归纳、大胆猜想和概括;
3、通过本课初步学会识别及构建基本图形、体会图形间的变化及联系,增强自己的识图和逻辑推理能力。
学习目标
两直线平行
{
1.同位角相等
2.内错角相等
3.同旁内角互补
性质
判定
1、由_________得到___________的结论是平行线的判定;
2、由____________得到______________的结论是平行线的性质.
用途:
用途:
角的关系
两直线平行
两直线位置关系的确定
两直线平行
角相等或互补
角的计算与证明
请注意:
知识回顾
如图,AB,CD是两根钉在木板上的平行木条,将一根橡皮筋
固定在A,C两点,点E是橡皮筋上的一点,拽动E点将橡皮筋
拉紧后,请你探索∠A,∠AEC,∠C之间具有怎样的关系并
说明理由.(提示:先画出示意图,再说明理由).
课堂引入
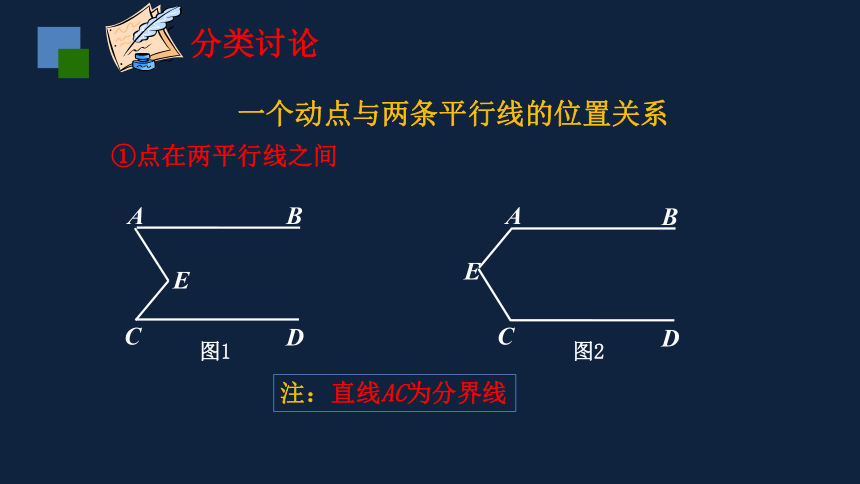
一个动点与两条平行线的位置关系
分析:
①点在两平行线之间
②点在两平行线之外
一个动点与两条平行线的位置关系
①点在两平行线之间
A
E
C
D
B
图1
A
E
C
D
B
图2
分类讨论
注:直线AC为分界线
A
E
C
D
B
图3
A
E
C
D
B
图4
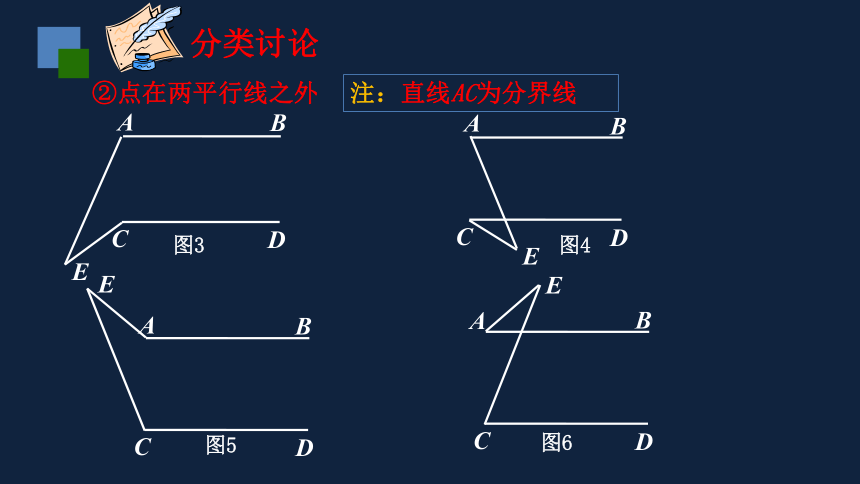
分类讨论
②点在两平行线之外
A
E
C
D
B
图6
A
E
C
D
B
图5
注:直线AC为分界线
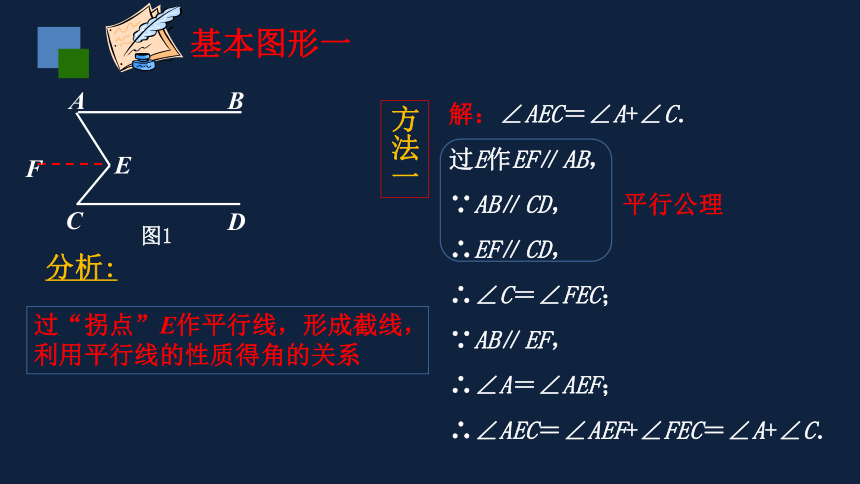
基本图形一
A
E
C
D
B
图1
F
解:∠AEC=∠A+∠C.
过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠C=∠FEC;
∵AB∥EF,
∴∠A=∠AEF;
∴∠AEC=∠AEF+∠FEC=∠A+∠C.
?
分析:
过“拐点”E作平行线,形成截线,
利用平行线的性质得角的关系
方法一
平行公理
A
E
C
D
B
图1
解:∠AEC=∠EAB+∠ECD.
连接AC,
∵AB∥CD,
∴∠BAC+∠ACD
=
180°,
即∠BAE+∠EAC
+∠ACE
+∠ECD
=
180°,
∵
∠AEC+∠EAC
+∠ACE
=
180°,
∴∠AEC=∠BAE+∠ECD.
?
分析:
连接AC,形成三角形AEC,利用三角形的内角和及平行线的性质
方法二
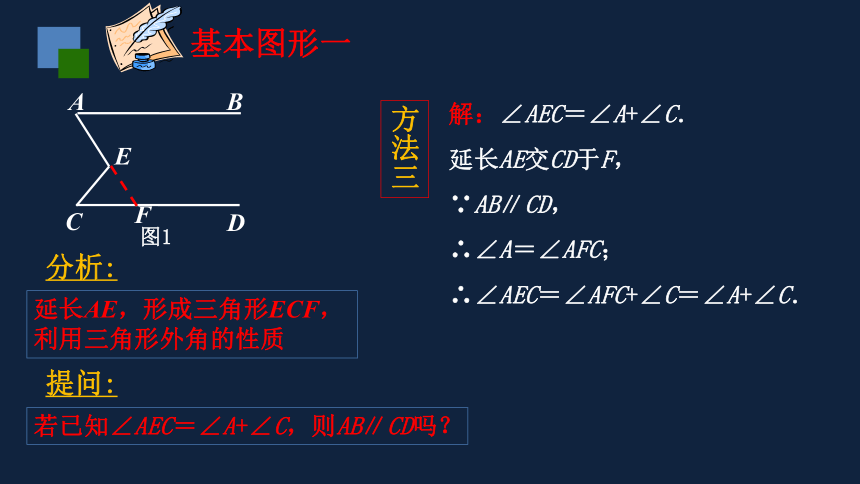
基本图形一
A
E
C
D
B
图1
F
解:∠AEC=∠A+∠C.
延长AE交CD于F,
∵AB∥CD,
∴∠A=∠AFC;
∴∠AEC=∠AFC+∠C=∠A+∠C.
?
分析:
延长AE,形成三角形ECF,
利用三角形外角的性质
方法三
提问:
若已知∠AEC=∠A+∠C,则AB∥CD吗?
基本图形一
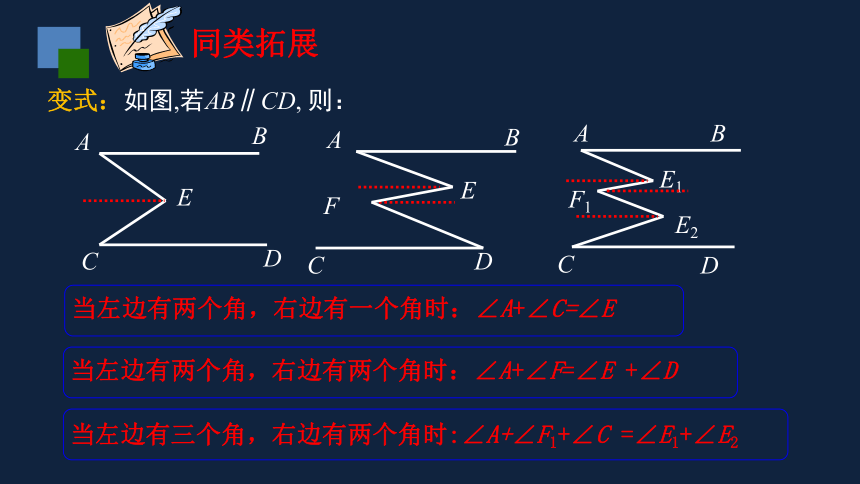
变式:如图,若AB∥CD,
则:
A
B
C
D
E
当左边有两个角,右边有一个角时:∠A+∠C=∠E
当左边有两个角,右边有两个角时:∠A+∠F=∠E
+∠D
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
当左边有三个角,右边有两个角时:∠A+∠F1+∠C
=∠E1+∠E2
同类拓展
C
A
B
D
E1
F1
E2
Em
F2
Fn
∠A+∠F1
+
∠
F2
+…+
∠Fn=
∠E1
+∠E2
+…+
∠Em+
∠D
当左边有n个角,右边有m个角时:
若左边有n个角,右边有m个角,你能找到规律吗?
同类拓展
分析:
过“拐点”E作平行线,形成截线,
利用平行线的性质得角的关系
方法一
A
E
C
D
B
图2
F
解:
∠AEC+∠EAB+∠ECD=360°,
过E作EF∥AB,则AB∥FE∥CD,
∴∠BAE+∠AEF=180°
∠CEF+∠ECD=180°,
∴∠BAE+∠AEF+∠CEF+∠ECD=360°,
即∠AEC+∠EAB+∠ECD=360°.
基本图形二
A
E
C
D
B
图2
解:
∠AEC+∠EAB+∠ECD=360°
连接AC,
∵AB∥CD,
∴∠BAC+∠ACD
=
180°,
∵
∠AEC+∠EAC
+∠ACE
=
180°,
∴∠BAC
+∠ACD
+∠EAC
+∠ACE
+∠AEC
=
360°,
即
∠AEC+∠EAB+∠ECD=360°
.
?
分析:
连接AC,形成三角形ACE,利用三角形的内角和及平行线的性质
方法二
基本图形二
A
E
C
D
B
图1
F
解:
∠AEC+∠EAB+∠ECD=360°
延长AE交CD反向延长线于F,
∵AB∥CD,
∴∠A=∠AFG;
∴∠AEC+∠EAB+∠ECD
=∠AFG+∠AEC+∠ECD
=
360°.
?
分析:
延长AE,形成三角形ECF,
利用三角形的外角和的性质
方法三
提问:
若已知∠AEC+∠EAB+∠ECD=360°,则AB∥CD吗?
G
基本图形二
变式:如图,AB∥CD,则
:
C
A
B
D
E
A
C
D
B
E2
E1
当有一个拐点时:
∠A+∠E+∠C=
360°
当有两个拐点时:
∠A+∠
E1
+
∠
E2
+∠C
=
540°
当有三个拐点时:
∠A+∠
E1
+
∠
E2
+∠
E3
+∠C
=
720°
A
B
C
D
E1
E2
E3
同类拓展
…
A
B
C
D
E1
E2
En
当有n个拐点时:
∠A+∠
E1
+
∠
E2
+…+∠
En
+∠C
=
180°
(n+1)
若有n个拐点,你能找到规律吗?
同类拓展
A
E
C
D
B
图3
分析:
过“拐点”E作平行线,形成截线,
利用平行线的性质得角的关系
方法一
F
解:∠C=∠A+∠AEC.
过E作EF∥AB,则AB∥FE∥CD,
∴∠C=∠CEF,∠A=∠AEF,
∵∠CEF=∠AEF+∠AEC,
∴∠C=∠A+∠AEC.
基本图形三
A
E
C
D
B
图3
分析:
方法二
F
解:∠ECD=∠A+∠E.
∵
AB∥CD,
∴∠ECD=∠CFB,
∵∠CFB=∠A+∠E,
∴
∠ECD=∠A+∠E
.
延长EC,形成三角形AEF,
利用三角形的外角的性质
提问:
若已知∠ECD=∠A+∠E
,则AB∥CD吗?
基本图形三
分析:
过“拐点”E作平行线,形成截线,
利用平行线的性质得角的关系
方法一
F
A
E
C
D
B
图4
解:∠A=∠C+∠AEC.
过E作EF∥AB,则AB∥FE∥CD,
∴∠C=∠CEF,∠A=∠AEF,
∵∠AEF=∠CEF+∠AEC,
∴∠A=∠C+∠AEC.
基本图形四
分析:
方法二
F
解:
∠A=∠C+∠E
.
∵
AB∥CD,
∴∠EFD=∠A,
∵∠EFD=∠C+∠E,
∴
∠A=∠C+∠E
.
找三角形CEF,
利用三角形的外角的性质
提问:
若已知∠A=∠C+∠E
,则AB∥CD吗?
A
E
C
D
B
图4
基本图形四
A
E
C
D
B
图6
A
E
C
D
B
图5
∠A=∠C+∠E
∠C=∠A+∠E
基本图形五、六
运用知识
例1:如图,已知AB∥DE,∠ABC=80°,∠CDE=150°,求∠BCD。
解:反向延长DE交BC于M,
∵AB∥DE,
∴∠BMD=∠ABC=80°,
∴∠CMD=180°﹣∠BMD=100°;
又∵∠CDE=∠CMD+∠BCD,
∴∠BCD=∠CDE﹣∠CMD
=150°﹣100°=50°.
【分析】根据两直线平行,内错角
相等以及三角形外角性质即可解答.
M
运用知识
例2:
如图,CD∥BE,则∠2+∠3﹣∠1的度数等于
.
解:如图,过A作AF∥CD,
∵CD∥BE,
∴AF∥BE,
∴∠3=∠BAF,
∴∠CAF=∠BAF﹣∠1=∠3﹣∠1,
∵AF∥CD,
∴∠CAF+∠2=180°,
∴∠3﹣∠1+∠2=180°
【分析】如图,过A作AF∥CD,依据平行线的性质,即可得到∠3=∠BAF,∠CAF+∠2=180°,进而得出∠2+∠3﹣∠1的度数.
180°
F
例3:如图,直线AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=50°,则∠GHM的大小是
。
B
A
G
M
E
F
C
P
H
N
D
运用知识
∠A+∠F1
+
∠
F2
+…+
∠Fn=
∠E1
+∠E2
+…+
∠Em+
∠D
当左边有n个角,右边有m个角时:
【分析】
∴∠BFG+∠GHM+∠MND=∠FGH+∠HMN
∴30°+∠GHM+50°=90°+30°
∴∠GHM=40°
40°
思维拓展
例4:如图,AB∥CD,∠EAF=14∠EAB,∠ECF=
14∠ECD,试探求∠AFC与∠AEC的关系。
?
B
A
D
C
E
F
【分析】
(1)由基本图形一得:∠AEC=∠EAB+∠ECD
(2)由基本图形一得:∠AFC=∠FAB+∠FCD
解:∵
∠EAF=14∠EAB,∠ECF=
14∠ECD
∴∠FAB=????4∠EAB,∠FCD=
????4∠ECD
∴∠AFC=∠FAB+∠FCD
=????4∠EAB+????4∠ECD
=????4(∠EAB+∠ECD)
=????4∠AEC
?
思维拓展
变式:如图,AB∥CD,∠EAF=1????∠EAB,∠ECF=
1????∠ECD,试探求∠AFC与∠AEC的关系。
?
B
A
D
C
E
F
【分析】
(1)由基本图形一得:∠AEC=∠EAB+∠ECD
(2)由基本图形一得:∠AFC=∠FAB+∠FCD
解:∵
∠EAF=1????∠EAB,∠ECF=1????∠ECD
∴∠FAB=?????????????∠EAB,∠FCD=?????????????∠ECD
∴∠AFC=∠FAB+∠FCD=?????????????∠EAB+?????????????∠ECD
=??????????????(∠EAB+∠ECD)
=?????????????∠AEC
?
思维拓展
【分析】
例5:已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=140?,则∠F=
。
(1)由基本图形一,你能得到∠F与∠1+∠3的关系吗?
(2)由基本图形二,你能得到∠ABE+∠CDE的值吗?
(3)由BF和DF分别平分∠ABE和∠CDE,你能得到
∠1+∠3
与∠ABE+∠CDE的关系吗?
解:由基本图形二得:
∠ABE+∠CDE+∠E=360°
∵∠E=140?
∴∠ABE+∠CDE=220?
∵
BF,DF分别平分∠ABE和∠CDE
∴∠1+∠3=110?
∴∠F=∠1+∠3=110?
110°
思维拓展
变式:将上题中的∠ABE的平分线改为它的补角∠ABG的平分线,其它条件不变,则∠F=
。
140?
解:由上题得:∠ABE+∠CDE=220°
∵
BF和DF分别平分∠ABC和∠CDE
∴
∠3-∠1=12[∠CDE-(180°-∠ABE
)]
=12(∠CDE+
∠ABE
-180°)
=20°
∴
∠F=∠3-∠1=20°
?
20°
方法一
【分析】
由基本图形四得:∠F=∠3-∠1
思维拓展
变式:将上题中的∠ABE的平分线改为它的补角∠ABG的平分线,其它条件不变,则∠F=
。
140?
20°
方法二
F’
【分析】
将两幅图相结合,寻找∠F与∠F’之间的关系
课堂小结
1、这节课你运用什么知识解决了问题?
(1)平行线的判定定理、性质定理,平行公理
(2)添加辅助线
2、你收获了什么?
(1)知识?
(2)方法?
(3)思想?
感谢大家
苏科版七年级下册
数学
几何学的光荣,在于它从很少几条独立
自主的原则出发,而得以完成如此多的
工作。
----牛顿
1、掌握平行线的性质,能运用平行线的判定与性质进行角的计算与证明;
2、在问题探究中,仔细观察、比较、联想、分析、归纳、大胆猜想和概括;
3、通过本课初步学会识别及构建基本图形、体会图形间的变化及联系,增强自己的识图和逻辑推理能力。
学习目标
两直线平行
{
1.同位角相等
2.内错角相等
3.同旁内角互补
性质
判定
1、由_________得到___________的结论是平行线的判定;
2、由____________得到______________的结论是平行线的性质.
用途:
用途:
角的关系
两直线平行
两直线位置关系的确定
两直线平行
角相等或互补
角的计算与证明
请注意:
知识回顾
如图,AB,CD是两根钉在木板上的平行木条,将一根橡皮筋
固定在A,C两点,点E是橡皮筋上的一点,拽动E点将橡皮筋
拉紧后,请你探索∠A,∠AEC,∠C之间具有怎样的关系并
说明理由.(提示:先画出示意图,再说明理由).
课堂引入
一个动点与两条平行线的位置关系
分析:
①点在两平行线之间
②点在两平行线之外
一个动点与两条平行线的位置关系
①点在两平行线之间
A
E
C
D
B
图1
A
E
C
D
B
图2
分类讨论
注:直线AC为分界线
A
E
C
D
B
图3
A
E
C
D
B
图4
分类讨论
②点在两平行线之外
A
E
C
D
B
图6
A
E
C
D
B
图5
注:直线AC为分界线
基本图形一
A
E
C
D
B
图1
F
解:∠AEC=∠A+∠C.
过E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠C=∠FEC;
∵AB∥EF,
∴∠A=∠AEF;
∴∠AEC=∠AEF+∠FEC=∠A+∠C.
?
分析:
过“拐点”E作平行线,形成截线,
利用平行线的性质得角的关系
方法一
平行公理
A
E
C
D
B
图1
解:∠AEC=∠EAB+∠ECD.
连接AC,
∵AB∥CD,
∴∠BAC+∠ACD
=
180°,
即∠BAE+∠EAC
+∠ACE
+∠ECD
=
180°,
∵
∠AEC+∠EAC
+∠ACE
=
180°,
∴∠AEC=∠BAE+∠ECD.
?
分析:
连接AC,形成三角形AEC,利用三角形的内角和及平行线的性质
方法二
基本图形一
A
E
C
D
B
图1
F
解:∠AEC=∠A+∠C.
延长AE交CD于F,
∵AB∥CD,
∴∠A=∠AFC;
∴∠AEC=∠AFC+∠C=∠A+∠C.
?
分析:
延长AE,形成三角形ECF,
利用三角形外角的性质
方法三
提问:
若已知∠AEC=∠A+∠C,则AB∥CD吗?
基本图形一
变式:如图,若AB∥CD,
则:
A
B
C
D
E
当左边有两个角,右边有一个角时:∠A+∠C=∠E
当左边有两个角,右边有两个角时:∠A+∠F=∠E
+∠D
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
当左边有三个角,右边有两个角时:∠A+∠F1+∠C
=∠E1+∠E2
同类拓展
C
A
B
D
E1
F1
E2
Em
F2
Fn
∠A+∠F1
+
∠
F2
+…+
∠Fn=
∠E1
+∠E2
+…+
∠Em+
∠D
当左边有n个角,右边有m个角时:
若左边有n个角,右边有m个角,你能找到规律吗?
同类拓展
分析:
过“拐点”E作平行线,形成截线,
利用平行线的性质得角的关系
方法一
A
E
C
D
B
图2
F
解:
∠AEC+∠EAB+∠ECD=360°,
过E作EF∥AB,则AB∥FE∥CD,
∴∠BAE+∠AEF=180°
∠CEF+∠ECD=180°,
∴∠BAE+∠AEF+∠CEF+∠ECD=360°,
即∠AEC+∠EAB+∠ECD=360°.
基本图形二
A
E
C
D
B
图2
解:
∠AEC+∠EAB+∠ECD=360°
连接AC,
∵AB∥CD,
∴∠BAC+∠ACD
=
180°,
∵
∠AEC+∠EAC
+∠ACE
=
180°,
∴∠BAC
+∠ACD
+∠EAC
+∠ACE
+∠AEC
=
360°,
即
∠AEC+∠EAB+∠ECD=360°
.
?
分析:
连接AC,形成三角形ACE,利用三角形的内角和及平行线的性质
方法二
基本图形二
A
E
C
D
B
图1
F
解:
∠AEC+∠EAB+∠ECD=360°
延长AE交CD反向延长线于F,
∵AB∥CD,
∴∠A=∠AFG;
∴∠AEC+∠EAB+∠ECD
=∠AFG+∠AEC+∠ECD
=
360°.
?
分析:
延长AE,形成三角形ECF,
利用三角形的外角和的性质
方法三
提问:
若已知∠AEC+∠EAB+∠ECD=360°,则AB∥CD吗?
G
基本图形二
变式:如图,AB∥CD,则
:
C
A
B
D
E
A
C
D
B
E2
E1
当有一个拐点时:
∠A+∠E+∠C=
360°
当有两个拐点时:
∠A+∠
E1
+
∠
E2
+∠C
=
540°
当有三个拐点时:
∠A+∠
E1
+
∠
E2
+∠
E3
+∠C
=
720°
A
B
C
D
E1
E2
E3
同类拓展
…
A
B
C
D
E1
E2
En
当有n个拐点时:
∠A+∠
E1
+
∠
E2
+…+∠
En
+∠C
=
180°
(n+1)
若有n个拐点,你能找到规律吗?
同类拓展
A
E
C
D
B
图3
分析:
过“拐点”E作平行线,形成截线,
利用平行线的性质得角的关系
方法一
F
解:∠C=∠A+∠AEC.
过E作EF∥AB,则AB∥FE∥CD,
∴∠C=∠CEF,∠A=∠AEF,
∵∠CEF=∠AEF+∠AEC,
∴∠C=∠A+∠AEC.
基本图形三
A
E
C
D
B
图3
分析:
方法二
F
解:∠ECD=∠A+∠E.
∵
AB∥CD,
∴∠ECD=∠CFB,
∵∠CFB=∠A+∠E,
∴
∠ECD=∠A+∠E
.
延长EC,形成三角形AEF,
利用三角形的外角的性质
提问:
若已知∠ECD=∠A+∠E
,则AB∥CD吗?
基本图形三
分析:
过“拐点”E作平行线,形成截线,
利用平行线的性质得角的关系
方法一
F
A
E
C
D
B
图4
解:∠A=∠C+∠AEC.
过E作EF∥AB,则AB∥FE∥CD,
∴∠C=∠CEF,∠A=∠AEF,
∵∠AEF=∠CEF+∠AEC,
∴∠A=∠C+∠AEC.
基本图形四
分析:
方法二
F
解:
∠A=∠C+∠E
.
∵
AB∥CD,
∴∠EFD=∠A,
∵∠EFD=∠C+∠E,
∴
∠A=∠C+∠E
.
找三角形CEF,
利用三角形的外角的性质
提问:
若已知∠A=∠C+∠E
,则AB∥CD吗?
A
E
C
D
B
图4
基本图形四
A
E
C
D
B
图6
A
E
C
D
B
图5
∠A=∠C+∠E
∠C=∠A+∠E
基本图形五、六
运用知识
例1:如图,已知AB∥DE,∠ABC=80°,∠CDE=150°,求∠BCD。
解:反向延长DE交BC于M,
∵AB∥DE,
∴∠BMD=∠ABC=80°,
∴∠CMD=180°﹣∠BMD=100°;
又∵∠CDE=∠CMD+∠BCD,
∴∠BCD=∠CDE﹣∠CMD
=150°﹣100°=50°.
【分析】根据两直线平行,内错角
相等以及三角形外角性质即可解答.
M
运用知识
例2:
如图,CD∥BE,则∠2+∠3﹣∠1的度数等于
.
解:如图,过A作AF∥CD,
∵CD∥BE,
∴AF∥BE,
∴∠3=∠BAF,
∴∠CAF=∠BAF﹣∠1=∠3﹣∠1,
∵AF∥CD,
∴∠CAF+∠2=180°,
∴∠3﹣∠1+∠2=180°
【分析】如图,过A作AF∥CD,依据平行线的性质,即可得到∠3=∠BAF,∠CAF+∠2=180°,进而得出∠2+∠3﹣∠1的度数.
180°
F
例3:如图,直线AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=50°,则∠GHM的大小是
。
B
A
G
M
E
F
C
P
H
N
D
运用知识
∠A+∠F1
+
∠
F2
+…+
∠Fn=
∠E1
+∠E2
+…+
∠Em+
∠D
当左边有n个角,右边有m个角时:
【分析】
∴∠BFG+∠GHM+∠MND=∠FGH+∠HMN
∴30°+∠GHM+50°=90°+30°
∴∠GHM=40°
40°
思维拓展
例4:如图,AB∥CD,∠EAF=14∠EAB,∠ECF=
14∠ECD,试探求∠AFC与∠AEC的关系。
?
B
A
D
C
E
F
【分析】
(1)由基本图形一得:∠AEC=∠EAB+∠ECD
(2)由基本图形一得:∠AFC=∠FAB+∠FCD
解:∵
∠EAF=14∠EAB,∠ECF=
14∠ECD
∴∠FAB=????4∠EAB,∠FCD=
????4∠ECD
∴∠AFC=∠FAB+∠FCD
=????4∠EAB+????4∠ECD
=????4(∠EAB+∠ECD)
=????4∠AEC
?
思维拓展
变式:如图,AB∥CD,∠EAF=1????∠EAB,∠ECF=
1????∠ECD,试探求∠AFC与∠AEC的关系。
?
B
A
D
C
E
F
【分析】
(1)由基本图形一得:∠AEC=∠EAB+∠ECD
(2)由基本图形一得:∠AFC=∠FAB+∠FCD
解:∵
∠EAF=1????∠EAB,∠ECF=1????∠ECD
∴∠FAB=?????????????∠EAB,∠FCD=?????????????∠ECD
∴∠AFC=∠FAB+∠FCD=?????????????∠EAB+?????????????∠ECD
=??????????????(∠EAB+∠ECD)
=?????????????∠AEC
?
思维拓展
【分析】
例5:已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=140?,则∠F=
。
(1)由基本图形一,你能得到∠F与∠1+∠3的关系吗?
(2)由基本图形二,你能得到∠ABE+∠CDE的值吗?
(3)由BF和DF分别平分∠ABE和∠CDE,你能得到
∠1+∠3
与∠ABE+∠CDE的关系吗?
解:由基本图形二得:
∠ABE+∠CDE+∠E=360°
∵∠E=140?
∴∠ABE+∠CDE=220?
∵
BF,DF分别平分∠ABE和∠CDE
∴∠1+∠3=110?
∴∠F=∠1+∠3=110?
110°
思维拓展
变式:将上题中的∠ABE的平分线改为它的补角∠ABG的平分线,其它条件不变,则∠F=
。
140?
解:由上题得:∠ABE+∠CDE=220°
∵
BF和DF分别平分∠ABC和∠CDE
∴
∠3-∠1=12[∠CDE-(180°-∠ABE
)]
=12(∠CDE+
∠ABE
-180°)
=20°
∴
∠F=∠3-∠1=20°
?
20°
方法一
【分析】
由基本图形四得:∠F=∠3-∠1
思维拓展
变式:将上题中的∠ABE的平分线改为它的补角∠ABG的平分线,其它条件不变,则∠F=
。
140?
20°
方法二
F’
【分析】
将两幅图相结合,寻找∠F与∠F’之间的关系
课堂小结
1、这节课你运用什么知识解决了问题?
(1)平行线的判定定理、性质定理,平行公理
(2)添加辅助线
2、你收获了什么?
(1)知识?
(2)方法?
(3)思想?
感谢大家
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
