7.4 认识三角形-2021春苏科版七年级数学下册课件(共43张PPT)
文档属性
| 名称 | 7.4 认识三角形-2021春苏科版七年级数学下册课件(共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 629.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览











文档简介
第七章 平面图形的认识(二)
一、认识三角形
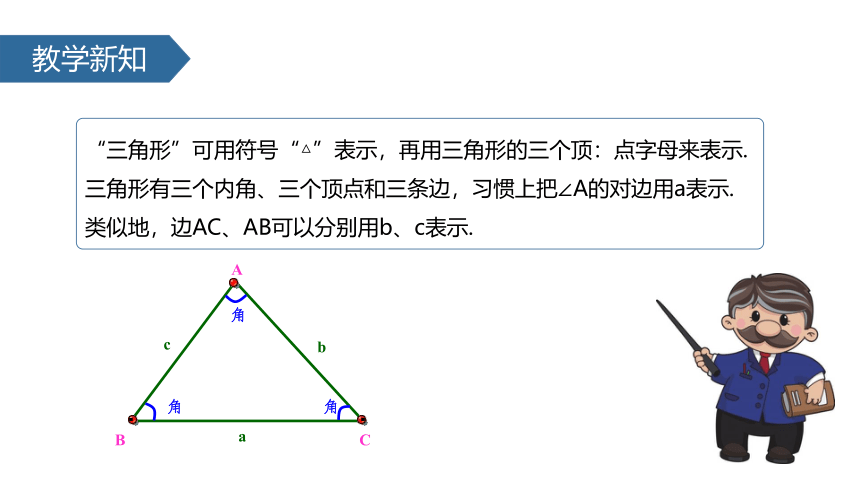
“三角形”可用符号“△”表示,再用三角形的三个顶:点字母来表示.
三角形有三个内角、三个顶点和三条边,习惯上把∠A的对边用a表示.类似地,边AC、AB可以分别用b、c表示.
c
b
a
A
B
角
角
角
C
教学新知
知识要点
2.能正确区分锐角三角形、直角三角形、钝角三角形,体悟分类的数学思想。
1.进一步认识三角形的概念及其基本要素,并能用符号语言表示三角形及其基本要素。
3.理解三角形三边之间的关系,并能用于解决相关的问题。
知识梳理
知识点1:三角形的基本概念
【例】在如图7.4-4所示的图形中,三角形的个数共有 个;以∠B为内角的三角形有 ; 在这两个三角形中,∠B的对边分别为_______ 和 .
图7.4-4
3
△ABC,△ABD
AC
AD
【讲解】按三角形的有关概念来,∠B、AB可以在不同的三角形中.
【方法小结】三角形的个数一定要注意要有顺序的去数,做到不重不漏.三角形有△ABC,△ABD,△ACD;∠B既在△ABC中,又在△ABD中,在△ABC中∠B的对边为AC,在△ABD中∠B的对边为AD.
知识梳理
A.连接任意三点组成的图形
B.由不在同一条直线上的三条线段首尾顺次相接所成的图形
B
C.由三条线段组成的图形
D.以上说法均不对
1.三角形是( )
2.如图7.4-5,(1)图中有 个三角形;这几个三角形分别表示为: 、 、 ;
(2)在ΔABC中,∠A的对边是 ;∠B的对边是 ;∠ACB的对边是 .
3
ΔABC
ΔACD
ΔCDB
a
b
AB
图7.4-5
【例】下列说法正确的是( )
知识梳理
知识点2 三角形的分类
A.一个直角三角形一定不是等腰三角形
B.一个等腰三角形一定不是锐角三角形
C.一个钝角三角形一定不是等腰三角形
D.一个等边三角形一定不是钝角三角形
D
【方法小结】根据三角形的分类方法进行分析判断.三角形按角分为锐角三角形、直角三角形和钝角三角形;三角形按边分为不等边三角形和等腰三角形(等边三角形).
知识梳理
【例】现有若干个三角形,在所有的内角中,有5个直角,3个钝角,25个锐角,则在这些三角形中锐角三角形的个数是( )
A.3 B.4或5 C.6或7 D.8
【参考答案】A.提示:由题意得:若干个三角形,在所有的内角中,有5个直角,3个钝角,25个锐角时,∴共有33÷3=11个三角形;又三角形中,最多有一个直角或最多有一个钝角,显然11个三角形中,有5个直角三角形和3个钝角三角形;故还有11-5-3=3个锐角三角形.故选A.
A
知识梳理
【例】下列每组数据分别是三根小木棒的长度,用它们能摆成三角形吗?
(1)6cm,8cm,10cm; (2)7cm,7cm,14cm;
(3)10cm,12cm,21cm。
【讲解】 (1)6+8>10;6+10>8;8+10>6,所以能构成三角形 .(2)因为7+7≯14,所以这3条线段不能构成三角形.(3)10+12>21;21+10>12;21+12>10,所以能构成三角形.
知识点3: 三角形的三边关系
知识梳理
【小练习】
(2011河北)已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为( )
A.2 B.3 C.5 D.13
B
2.有长度分别为2cm、 3cm、 4cm和5cm的4根小木棒,任取其中3根,你可以搭出几种不同的三角形?
知识梳理
2.有长度分别为2cm、 3cm、 4cm和5cm的4根小木棒,任取其中3根,你可以搭出几种不同的三角形?
【参考答案】
(1)三根木棒长是2cm、 3cm、 4cm时,因为2+3>4,所以能构成三角形;(2)三根木棒长是2cm、 3cm、 5cm时,因为2+3=5,所以不能构成三角形;(3)三根木棒长是2cm、 4cm、 5cm时,因为2+4>5,所以能构成三角形;(4)三根木棒长是3cm、 4cm、 5cm时,因为3+4>5,所以能构成三角形.
知识梳理
知识点1:三角形中的重要线段.
【例】下面四个图中,画ΔABC一边上的高,下列画法正确的是( )
A
B
D
C
C
知识梳理
【讲解】A选项中垂线段过顶点C应该与AB垂直,但图中CD与BC垂直,与三角形的高的概念不符,B选项中垂线段过顶点B应该与AC垂直,但图中BD与BC垂直,与三角形的高的概念不符,D选项中垂线段过顶点A应该与BC垂直,但图中AD与AC垂直,与三角形的高的概念不符,故选C.
【方法小结】作三角形的高:一要过三角形的顶点,二要与这个顶点的对边垂直.
知识梳理
知识点2: 三角形中的重要线段性质的应用.
【例】如图7.4-19,有一块三角形的优良品种实验土地,现引进四个良种进行对比实验,需将这块土地分成面积相等的四块。请你制订出二种以上的划分方案供选择(画图说明).
图7.4-19
知识梳理
【讲解】只要面积相等,形状不一定相同!本题就是通过“等底等高的三角形面积相等” 按此思路来画三角形即可,本题的画法很多.
方案如下:(1)如图7.4-20(1)中,点C、D、E分别是AB的四等分点;(2)如图7.4-20(2)中,C、D、E分别是三边的中点;(3)如图7.4-20(3)中,C点为AB的四等分点(靠近点A),E、F分别是BD边上的三等分点.
A
B
D
C
E
(2)
(1)
C
D
E
(3)
A
B
C
D
E
F
图7.4-20
知识梳理
【小练习】如图7.4-21,在△ABC中,已知点D,E,F分别是BC、AD、CE的中点,且??????????????????=4cm2,则 的值为( )
?
B
A.2cm2 B.1cm2 C.12cm2 D.14cm2
?
图7.4-21
中考在线
考点: 三角形的三边关系的应用.
【例】(2014?西宁)下列线段能构成三角形的是( )
A.2,2,4 B.3,4,5 C.1,2,3 D.2,3,6
【讲解】 A、2+2=4,不能构成三角形,故本选项错误;
B、3、4、5,能构成三角形,故本选项正确;
C、1+2=3,不能构成三角形,故本选项错误;
D、2+3<6,不能构成三角形,故本选项错误.
B
【方法小结】熟记三角形的任意两边之和大于第三边,两边之差小于第三边是解题的关键.根据三角形的任意两边之和大于第三边,对各选项的数据进行判断即可.
中考在线
1(2015?泉州)已知△ABC中,AB=6,BC=4,那么边AC的长可能是下列的哪个值( )
A.11 B.5 C.2 D.1
2.(2013?梧州)下列各组线段的长为边,能组成三角形的是( )
A.2cm,3cm,4cm B.2cm,3cm,5cm
C.2cm,5cm,10cm D.8cm,4cm,4cm
B
A
中考在线
3.(2013?淮安)若等腰三角形有两条边的长度为3和1,则此等腰三角形的周长为( )
A.5 B.7 C.5或7 D.6.
4. (2013?雅安)若(a-1)2+|b-2|=0,则以a、b为边长的等腰三角形的周长为 .
B
5
【参考答案】5,提示:运用非负数的性质、等腰三角形的性质以及三角形的三边关系,首先要根据非负数的性质得出边长,再运用分类讨论求解.
中考在线
考点1:三角形中的三条重要线段的认识.
【例】(2012山东省德州)不一定在三角形内部的线段是( )
A.三角形的角平分线 B.三角形的中线
C.三角形的高 D.三角形的中位线
【讲解】三角形的角平分线、中线、中位线都在三角形的内部,只有高可能在内部或者在外部,故选C
C
【方法小结】当三角形为锐角三角形时,三条高在三角形内部,当三角形是直角三角形时,两条高是三角形的直角边,一条高在三角形内部,当三角形为钝角三角形时,两条高在三角形内部,一条高在内部.
知识梳理
【例】(2015湖南省长沙)过 的顶点 ,作 边上的高,以下作法正确的是( )
A
B
A
D
C
知识梳理
【例】(2013山东济南)如图7.4-23,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S△ABC=6,则S1-S2=_________。
A
B
C
D
E
F
图7.4-23
1
考点2:三角形中的三条重要线段的应用 .
知识梳理
【讲解】将△ADF加上四边形BDFE补成△ABE,△CEF加上四边形BDFE补成△BCD.
【解】∵AD=2BD,BE=CE,
∴??????????????????=12??????????????????=3,??????????????????=13??????????????????=2,
∴S1+??????????????????????=3,S2+??????????????????????=2,
∴S1-S2=3-2=1.
?
【方法小结】三角形的中线平分三角形的面积,高相等的三角形的面积之比等于其底之比.
知识梳理
【例】(2012四川巴中)三角形的下列线段中能将三角形的面积分成相等的两部分的是( )
A.中线 B.角平分线 C.高 D.中位线
A
课堂练习
1.如图7.4-6,小明从家到学校有①②③三条路可走,每条路的长分别为a,b,c,则( )
A.a>b>c B.a>c>b C.a=b>c D.a=b<c
图7.4-6
D
课堂练习
2. 有两根长度分别为4cm和7cm的木棒,
(1)再取一根长度为2cm的木棒,它们能摆成三角形吗?为什么?
(2)如果取一根长度为11cm的木棒呢?
(3)你能取一根木棒,与原来的两根木棒摆成三角形吗?
【参考答案】(1)取长度为2cm的木棒时,由于2+4=6<7出现了两边之和小于第三边的情况,所以不能摆成三角形.(2)取长度为11cm的木棒时,由于4+7=11,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.(3)大于3cm且小于11cm.
课堂练习
3.被公认为目前“世界第一高人”的土耳其公民苏坦科森身高2.51米,若他的腿长为1.3米,他一步(两脚着地时两脚的间距)能迈3米多?你相信吗?
【参考答案】不能,因为1.3+1.3<3.
4. 如图7.4-7中的三角形有( )
A.4个 B.6个 C.8个 D.10个
图7.4-7
C
课堂练习
5. 以下列各组线段为边,能组成三角形的是( )
A.1 cm ,2cm , 4cm B.4 cm , 6 cm , 8 cm
C.5 cm, 6 cm, 12 cm D.2 cm, 3 cm, 5 cm
6. 若△ABC的三边长分别为整数,周长为11,且有一边为4,则这个三角形的最大边长为( )
A.7 B.6 C.5 D.4
7. 三角形的角平分线是( )
A.直线 B.射线 C.线段 D.射线或线段
C
B
C
课堂练习
8. 小华在电话中问小明:“已知一个钝角三角形,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解。”小华根据小明的提示,作出的图形正确的是( )
C
课堂练习
10. 如图7.4-24,AE⊥BC,垂足为E,以AE为高的三角形有
.
A
B
C
E
图7.4-24
D
△ABC、△ADC、△ABD、△ADE、△ACE、△ABE
9. 如图7.4-8所示,在△ABE中,AE所对的角是_________.
图7.4-8
∠B
课堂练习
11.如图7.4-25,在△ABC中,AD是中线,把△ADC沿AD折叠成图,则△AC1E △BED的面积(填“>”“<”“=”)。
A
B
C
图7.4-25
D
A
B
D
C1
E
=
课堂练习
12.下列三角形分别是什么三角形?
(1)已知这个三角形的两个内角分别是35°和55°;
(2)已知这个三角形的两条边长分别是6cm和6cm。
【参考答案】(1)是直角三角形.因为三角形内角和是180°,而两个内角分别是35°和55°,所以第三个角是90°,即这个三角形是直角三角形.
(2)是等腰三角形.因为两条边长分别是6cm和6cm,即有两边相等.若第三边长是6cm,则此三角形可进一步确定是等边三角形,否则只能判断是是等腰三角形.
课堂练习
13. 如图7.4-26,在△ABC中,AB=AC.
(1)在图上分别画出AB,AC边上的高CF和BE;
(2)填空:S??ABC=12AC×_______,S??ABC=12AB×_______.
(3)BE_______CF(填“=”“>”或“<”)
(4)由此可以得出结论:____________________________.
?
BE
CF
=
等腰三角形两腰上的高相等
图7.4-26
┐
┌
F
E
课后习题
1. 如图7.4-9所示,图中以∠B为内角的三角形的个数共有( )
A.1个 B.2个 C.3 个 D.4个
图7.4-9
B
课后习题
有( )
A. 6个 B. 5个 C. 4 个 D. 3个
3. 如图7.4-27,AD⊥BC,GC⊥BC,CF⊥AB,D、C、F是垂足,则下列说法中错误的是( )
A.△ABC中,AD是BC边上的高 B.△ABC中,GC是BC边上的高
C.△GBC中,GC是BC边上的高 D.△GBC中,CF是BG边上的高
B
D
2.已知三角形的三边长分别为3、8、x,若x的值为偶数,则x的值
图7.4-27
课后习题
4. 如图7.4-28所示,已知AE是△ABD的角平分线,AF是△ACD的角平分线,则下列结论不正确的是( )
A.∠EAF=12∠CAB B.∠DAF =12∠DAC
C.∠DAF=12∠EAF D.∠EAD= 12∠BAD
?
C
图7.4-28
课后习题
5. 已知三角形的两边长分别是2cm和6cm,第三边长是奇数,则第三边的长是________.
5或7
6. 如图7.4-10中有 个三角形.
图7.4-10
8
课后习题
7. 如图7.4-29,BD是△ABC的中线,AD=2,AB+BC=5,则△ABC的周长是 .
9
图7.4-29
课后习题
8. 已知,如图7.4-11,△ABC的内部有任意一点P,连接PB、PC,试说明:PB+PC图7.4-11
【参考答案】解:延长BP交AC于D,在△ABD中,BD课后习题
9. 已知△ABC的三边长为a,b、c,化简:
︱a+b-c︱-︱b-a-c︱的结果是( )
A. 2a B.-2 b C. 2a+2b D. 2b-2c
10. 等腰三角形的一边长为3,周长为11,则一腰长为 。
D
3或4
【参考答案】37.提示:第1个图形中有1个三角形,第2个图形中有5个三角形,第3个图形中有9个三角形,第4个图形中有13个三角形,……第10个图形中有1+4×9=37个三角形
课后习题
11. 观察图7.4-12中的一组图形,根据其变化规律,可得到该组图形中第10个图形的三角形个数为 。
图7.4-12
37
图7.4-30
课后习题
12. 如图7.4-30,已知△ABC.
(1)画△ABC的角平分线AD;
(2)过点D画△ABD的高DE,过点D画△ACD的高DF;
(3)量出DE、DF的长度,你有怎样的发现?用语言表达出来.
【参考答案】
(1)△ABC的角平分线AD如图7.4-37所示;
(2)△ABD的高DE,△ACD的高DF如图7.4-37所示;(3)结论:角平分线上的点到角的两边距离相等。
课后习题
13.三条线段能构成三角形的条件是:任意两条线段长度的和大于第三条线段的长度.现有长为144cm的铁丝,要截成n小段(n>2),每段的长度都是不小于1cm的整数,如果其中任意三小段都不能拼成三角形,则n的最大值为多少?.
【参考答案】∵每段的长为不小于1(cm)的整数,∴最小的边最小是1,∵三条线段不能构成三角形,则第二段是1,第三段是2,第四段与第二、第三段不能构成三角形,则第四边最小是3,第五边是5,依次是8,13,21,34,55,再大时,各个小段的和大于150cm,不满足条件.上述这些数之和为143,与144相差1,故可取1,1,2,3,5,8,13,21,34,56,这时n的值最大,n=10.
课后习题
14. 如图7.4-32所示,中华门中学有一块三角形空地,要在这块空地上种植某种草皮以美化校园,已知这种草皮每平方米的售价为a元,根据图中所标尺寸,购买这种草皮至少要花( )元?
C
图7.4-32
A.50a B.75a C.150a D.300a
一、认识三角形
“三角形”可用符号“△”表示,再用三角形的三个顶:点字母来表示.
三角形有三个内角、三个顶点和三条边,习惯上把∠A的对边用a表示.类似地,边AC、AB可以分别用b、c表示.
c
b
a
A
B
角
角
角
C
教学新知
知识要点
2.能正确区分锐角三角形、直角三角形、钝角三角形,体悟分类的数学思想。
1.进一步认识三角形的概念及其基本要素,并能用符号语言表示三角形及其基本要素。
3.理解三角形三边之间的关系,并能用于解决相关的问题。
知识梳理
知识点1:三角形的基本概念
【例】在如图7.4-4所示的图形中,三角形的个数共有 个;以∠B为内角的三角形有 ; 在这两个三角形中,∠B的对边分别为_______ 和 .
图7.4-4
3
△ABC,△ABD
AC
AD
【讲解】按三角形的有关概念来,∠B、AB可以在不同的三角形中.
【方法小结】三角形的个数一定要注意要有顺序的去数,做到不重不漏.三角形有△ABC,△ABD,△ACD;∠B既在△ABC中,又在△ABD中,在△ABC中∠B的对边为AC,在△ABD中∠B的对边为AD.
知识梳理
A.连接任意三点组成的图形
B.由不在同一条直线上的三条线段首尾顺次相接所成的图形
B
C.由三条线段组成的图形
D.以上说法均不对
1.三角形是( )
2.如图7.4-5,(1)图中有 个三角形;这几个三角形分别表示为: 、 、 ;
(2)在ΔABC中,∠A的对边是 ;∠B的对边是 ;∠ACB的对边是 .
3
ΔABC
ΔACD
ΔCDB
a
b
AB
图7.4-5
【例】下列说法正确的是( )
知识梳理
知识点2 三角形的分类
A.一个直角三角形一定不是等腰三角形
B.一个等腰三角形一定不是锐角三角形
C.一个钝角三角形一定不是等腰三角形
D.一个等边三角形一定不是钝角三角形
D
【方法小结】根据三角形的分类方法进行分析判断.三角形按角分为锐角三角形、直角三角形和钝角三角形;三角形按边分为不等边三角形和等腰三角形(等边三角形).
知识梳理
【例】现有若干个三角形,在所有的内角中,有5个直角,3个钝角,25个锐角,则在这些三角形中锐角三角形的个数是( )
A.3 B.4或5 C.6或7 D.8
【参考答案】A.提示:由题意得:若干个三角形,在所有的内角中,有5个直角,3个钝角,25个锐角时,∴共有33÷3=11个三角形;又三角形中,最多有一个直角或最多有一个钝角,显然11个三角形中,有5个直角三角形和3个钝角三角形;故还有11-5-3=3个锐角三角形.故选A.
A
知识梳理
【例】下列每组数据分别是三根小木棒的长度,用它们能摆成三角形吗?
(1)6cm,8cm,10cm; (2)7cm,7cm,14cm;
(3)10cm,12cm,21cm。
【讲解】 (1)6+8>10;6+10>8;8+10>6,所以能构成三角形 .(2)因为7+7≯14,所以这3条线段不能构成三角形.(3)10+12>21;21+10>12;21+12>10,所以能构成三角形.
知识点3: 三角形的三边关系
知识梳理
【小练习】
(2011河北)已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形个数为( )
A.2 B.3 C.5 D.13
B
2.有长度分别为2cm、 3cm、 4cm和5cm的4根小木棒,任取其中3根,你可以搭出几种不同的三角形?
知识梳理
2.有长度分别为2cm、 3cm、 4cm和5cm的4根小木棒,任取其中3根,你可以搭出几种不同的三角形?
【参考答案】
(1)三根木棒长是2cm、 3cm、 4cm时,因为2+3>4,所以能构成三角形;(2)三根木棒长是2cm、 3cm、 5cm时,因为2+3=5,所以不能构成三角形;(3)三根木棒长是2cm、 4cm、 5cm时,因为2+4>5,所以能构成三角形;(4)三根木棒长是3cm、 4cm、 5cm时,因为3+4>5,所以能构成三角形.
知识梳理
知识点1:三角形中的重要线段.
【例】下面四个图中,画ΔABC一边上的高,下列画法正确的是( )
A
B
D
C
C
知识梳理
【讲解】A选项中垂线段过顶点C应该与AB垂直,但图中CD与BC垂直,与三角形的高的概念不符,B选项中垂线段过顶点B应该与AC垂直,但图中BD与BC垂直,与三角形的高的概念不符,D选项中垂线段过顶点A应该与BC垂直,但图中AD与AC垂直,与三角形的高的概念不符,故选C.
【方法小结】作三角形的高:一要过三角形的顶点,二要与这个顶点的对边垂直.
知识梳理
知识点2: 三角形中的重要线段性质的应用.
【例】如图7.4-19,有一块三角形的优良品种实验土地,现引进四个良种进行对比实验,需将这块土地分成面积相等的四块。请你制订出二种以上的划分方案供选择(画图说明).
图7.4-19
知识梳理
【讲解】只要面积相等,形状不一定相同!本题就是通过“等底等高的三角形面积相等” 按此思路来画三角形即可,本题的画法很多.
方案如下:(1)如图7.4-20(1)中,点C、D、E分别是AB的四等分点;(2)如图7.4-20(2)中,C、D、E分别是三边的中点;(3)如图7.4-20(3)中,C点为AB的四等分点(靠近点A),E、F分别是BD边上的三等分点.
A
B
D
C
E
(2)
(1)
C
D
E
(3)
A
B
C
D
E
F
图7.4-20
知识梳理
【小练习】如图7.4-21,在△ABC中,已知点D,E,F分别是BC、AD、CE的中点,且??????????????????=4cm2,则 的值为( )
?
B
A.2cm2 B.1cm2 C.12cm2 D.14cm2
?
图7.4-21
中考在线
考点: 三角形的三边关系的应用.
【例】(2014?西宁)下列线段能构成三角形的是( )
A.2,2,4 B.3,4,5 C.1,2,3 D.2,3,6
【讲解】 A、2+2=4,不能构成三角形,故本选项错误;
B、3、4、5,能构成三角形,故本选项正确;
C、1+2=3,不能构成三角形,故本选项错误;
D、2+3<6,不能构成三角形,故本选项错误.
B
【方法小结】熟记三角形的任意两边之和大于第三边,两边之差小于第三边是解题的关键.根据三角形的任意两边之和大于第三边,对各选项的数据进行判断即可.
中考在线
1(2015?泉州)已知△ABC中,AB=6,BC=4,那么边AC的长可能是下列的哪个值( )
A.11 B.5 C.2 D.1
2.(2013?梧州)下列各组线段的长为边,能组成三角形的是( )
A.2cm,3cm,4cm B.2cm,3cm,5cm
C.2cm,5cm,10cm D.8cm,4cm,4cm
B
A
中考在线
3.(2013?淮安)若等腰三角形有两条边的长度为3和1,则此等腰三角形的周长为( )
A.5 B.7 C.5或7 D.6.
4. (2013?雅安)若(a-1)2+|b-2|=0,则以a、b为边长的等腰三角形的周长为 .
B
5
【参考答案】5,提示:运用非负数的性质、等腰三角形的性质以及三角形的三边关系,首先要根据非负数的性质得出边长,再运用分类讨论求解.
中考在线
考点1:三角形中的三条重要线段的认识.
【例】(2012山东省德州)不一定在三角形内部的线段是( )
A.三角形的角平分线 B.三角形的中线
C.三角形的高 D.三角形的中位线
【讲解】三角形的角平分线、中线、中位线都在三角形的内部,只有高可能在内部或者在外部,故选C
C
【方法小结】当三角形为锐角三角形时,三条高在三角形内部,当三角形是直角三角形时,两条高是三角形的直角边,一条高在三角形内部,当三角形为钝角三角形时,两条高在三角形内部,一条高在内部.
知识梳理
【例】(2015湖南省长沙)过 的顶点 ,作 边上的高,以下作法正确的是( )
A
B
A
D
C
知识梳理
【例】(2013山东济南)如图7.4-23,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S△ABC=6,则S1-S2=_________。
A
B
C
D
E
F
图7.4-23
1
考点2:三角形中的三条重要线段的应用 .
知识梳理
【讲解】将△ADF加上四边形BDFE补成△ABE,△CEF加上四边形BDFE补成△BCD.
【解】∵AD=2BD,BE=CE,
∴??????????????????=12??????????????????=3,??????????????????=13??????????????????=2,
∴S1+??????????????????????=3,S2+??????????????????????=2,
∴S1-S2=3-2=1.
?
【方法小结】三角形的中线平分三角形的面积,高相等的三角形的面积之比等于其底之比.
知识梳理
【例】(2012四川巴中)三角形的下列线段中能将三角形的面积分成相等的两部分的是( )
A.中线 B.角平分线 C.高 D.中位线
A
课堂练习
1.如图7.4-6,小明从家到学校有①②③三条路可走,每条路的长分别为a,b,c,则( )
A.a>b>c B.a>c>b C.a=b>c D.a=b<c
图7.4-6
D
课堂练习
2. 有两根长度分别为4cm和7cm的木棒,
(1)再取一根长度为2cm的木棒,它们能摆成三角形吗?为什么?
(2)如果取一根长度为11cm的木棒呢?
(3)你能取一根木棒,与原来的两根木棒摆成三角形吗?
【参考答案】(1)取长度为2cm的木棒时,由于2+4=6<7出现了两边之和小于第三边的情况,所以不能摆成三角形.(2)取长度为11cm的木棒时,由于4+7=11,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.(3)大于3cm且小于11cm.
课堂练习
3.被公认为目前“世界第一高人”的土耳其公民苏坦科森身高2.51米,若他的腿长为1.3米,他一步(两脚着地时两脚的间距)能迈3米多?你相信吗?
【参考答案】不能,因为1.3+1.3<3.
4. 如图7.4-7中的三角形有( )
A.4个 B.6个 C.8个 D.10个
图7.4-7
C
课堂练习
5. 以下列各组线段为边,能组成三角形的是( )
A.1 cm ,2cm , 4cm B.4 cm , 6 cm , 8 cm
C.5 cm, 6 cm, 12 cm D.2 cm, 3 cm, 5 cm
6. 若△ABC的三边长分别为整数,周长为11,且有一边为4,则这个三角形的最大边长为( )
A.7 B.6 C.5 D.4
7. 三角形的角平分线是( )
A.直线 B.射线 C.线段 D.射线或线段
C
B
C
课堂练习
8. 小华在电话中问小明:“已知一个钝角三角形,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解。”小华根据小明的提示,作出的图形正确的是( )
C
课堂练习
10. 如图7.4-24,AE⊥BC,垂足为E,以AE为高的三角形有
.
A
B
C
E
图7.4-24
D
△ABC、△ADC、△ABD、△ADE、△ACE、△ABE
9. 如图7.4-8所示,在△ABE中,AE所对的角是_________.
图7.4-8
∠B
课堂练习
11.如图7.4-25,在△ABC中,AD是中线,把△ADC沿AD折叠成图,则△AC1E △BED的面积(填“>”“<”“=”)。
A
B
C
图7.4-25
D
A
B
D
C1
E
=
课堂练习
12.下列三角形分别是什么三角形?
(1)已知这个三角形的两个内角分别是35°和55°;
(2)已知这个三角形的两条边长分别是6cm和6cm。
【参考答案】(1)是直角三角形.因为三角形内角和是180°,而两个内角分别是35°和55°,所以第三个角是90°,即这个三角形是直角三角形.
(2)是等腰三角形.因为两条边长分别是6cm和6cm,即有两边相等.若第三边长是6cm,则此三角形可进一步确定是等边三角形,否则只能判断是是等腰三角形.
课堂练习
13. 如图7.4-26,在△ABC中,AB=AC.
(1)在图上分别画出AB,AC边上的高CF和BE;
(2)填空:S??ABC=12AC×_______,S??ABC=12AB×_______.
(3)BE_______CF(填“=”“>”或“<”)
(4)由此可以得出结论:____________________________.
?
BE
CF
=
等腰三角形两腰上的高相等
图7.4-26
┐
┌
F
E
课后习题
1. 如图7.4-9所示,图中以∠B为内角的三角形的个数共有( )
A.1个 B.2个 C.3 个 D.4个
图7.4-9
B
课后习题
有( )
A. 6个 B. 5个 C. 4 个 D. 3个
3. 如图7.4-27,AD⊥BC,GC⊥BC,CF⊥AB,D、C、F是垂足,则下列说法中错误的是( )
A.△ABC中,AD是BC边上的高 B.△ABC中,GC是BC边上的高
C.△GBC中,GC是BC边上的高 D.△GBC中,CF是BG边上的高
B
D
2.已知三角形的三边长分别为3、8、x,若x的值为偶数,则x的值
图7.4-27
课后习题
4. 如图7.4-28所示,已知AE是△ABD的角平分线,AF是△ACD的角平分线,则下列结论不正确的是( )
A.∠EAF=12∠CAB B.∠DAF =12∠DAC
C.∠DAF=12∠EAF D.∠EAD= 12∠BAD
?
C
图7.4-28
课后习题
5. 已知三角形的两边长分别是2cm和6cm,第三边长是奇数,则第三边的长是________.
5或7
6. 如图7.4-10中有 个三角形.
图7.4-10
8
课后习题
7. 如图7.4-29,BD是△ABC的中线,AD=2,AB+BC=5,则△ABC的周长是 .
9
图7.4-29
课后习题
8. 已知,如图7.4-11,△ABC的内部有任意一点P,连接PB、PC,试说明:PB+PC
【参考答案】解:延长BP交AC于D,在△ABD中,BD
9. 已知△ABC的三边长为a,b、c,化简:
︱a+b-c︱-︱b-a-c︱的结果是( )
A. 2a B.-2 b C. 2a+2b D. 2b-2c
10. 等腰三角形的一边长为3,周长为11,则一腰长为 。
D
3或4
【参考答案】37.提示:第1个图形中有1个三角形,第2个图形中有5个三角形,第3个图形中有9个三角形,第4个图形中有13个三角形,……第10个图形中有1+4×9=37个三角形
课后习题
11. 观察图7.4-12中的一组图形,根据其变化规律,可得到该组图形中第10个图形的三角形个数为 。
图7.4-12
37
图7.4-30
课后习题
12. 如图7.4-30,已知△ABC.
(1)画△ABC的角平分线AD;
(2)过点D画△ABD的高DE,过点D画△ACD的高DF;
(3)量出DE、DF的长度,你有怎样的发现?用语言表达出来.
【参考答案】
(1)△ABC的角平分线AD如图7.4-37所示;
(2)△ABD的高DE,△ACD的高DF如图7.4-37所示;(3)结论:角平分线上的点到角的两边距离相等。
课后习题
13.三条线段能构成三角形的条件是:任意两条线段长度的和大于第三条线段的长度.现有长为144cm的铁丝,要截成n小段(n>2),每段的长度都是不小于1cm的整数,如果其中任意三小段都不能拼成三角形,则n的最大值为多少?.
【参考答案】∵每段的长为不小于1(cm)的整数,∴最小的边最小是1,∵三条线段不能构成三角形,则第二段是1,第三段是2,第四段与第二、第三段不能构成三角形,则第四边最小是3,第五边是5,依次是8,13,21,34,55,再大时,各个小段的和大于150cm,不满足条件.上述这些数之和为143,与144相差1,故可取1,1,2,3,5,8,13,21,34,56,这时n的值最大,n=10.
课后习题
14. 如图7.4-32所示,中华门中学有一块三角形空地,要在这块空地上种植某种草皮以美化校园,已知这种草皮每平方米的售价为a元,根据图中所标尺寸,购买这种草皮至少要花( )元?
C
图7.4-32
A.50a B.75a C.150a D.300a
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
