北师大版八年级数学下册1.1 等腰三角形专题:分类讨论题型学案(含答案)
文档属性
| 名称 | 北师大版八年级数学下册1.1 等腰三角形专题:分类讨论题型学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 168.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 11:08:45 | ||
图片预览


文档简介
1210310010579100《三角形的证明》题型解读2 等腰三角形专题:分类讨论题型
【方法梳理】
1.“两定一动”情形:“两圆一线”;
2.所有情形:分三边两两相等分别论证解答;
3.解题思维习惯:先分情况、再画图形、最后由易到难顺序依次解答;
【典型例题】
例1.如图,长方形OABC,O是原点,点A、C分别在坐标轴上,OA=BC=10,AB=OC=8,在OC边上取一点D,将长方形沿AD折叠,使点O落在BC边上的点E处,连接ED并延长交x轴于点F.
(1)直接写出A、B两点的坐标;
(2)求出线段OD的长和直线DE的解析式;DO=5,
(3)在x轴上是否存在一点P,使△ADP为以AD为腰的等腰三角形,若存在,求出P点坐标;若不存在,请说明理由;
(4)点Q由O点出发,以每秒2个单位长度沿OD向D点运动,到达D点时运动终止,设△QDF的面积为S,设Q运动的时间为t,求出S与t的函数关系式;
解析: (1)A(10,0),B(0,8)
(2)设OD=x,由题可知CD=8-x,DE=x,在Rt△ABE中,AE=OA=10,AB=8,由勾股定理可得BE=6,则CE=4,在Rt△CDE中,由CD2+CE2=DE2可得42+(8-x)2=x2,解得x=5,即OD=5,由D(0,5)、E(4,8)可得直线DE的解析式为y=34x+5.
(3)由于题目明确AD为腰,所以只需要画“两圆”。由(2)可知AD=55,
①以A为圆心,AD为半径画圆,与x轴有两个交点P1,P2,则AP=AD=55,则OP=10±55,
∴P点坐标为(10+55,0)或(10-55,0)
②以D为圆心,AD为半径画圆,与x轴有两个交点P3,P4(P4与点A重合,舍去),
连接DP3,由AD=DP3可得O P3=OA=10,∴P3 (-10,0)
综上所述,点P的坐标为(-10,0)、(10+55,0)或(10-55,0).
(4)由直线DE的解析式y=34x+5可得F点的坐标为(-203,0),由题可知DQ=5-2t,
∴S?QDF=12?DQ?OF=12×2035-2t=-203t+503
例2.如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒2cm的速度沿折线A-B-C-A运动,设运动时间为t秒(t>0),
(1)AC=_______cm;
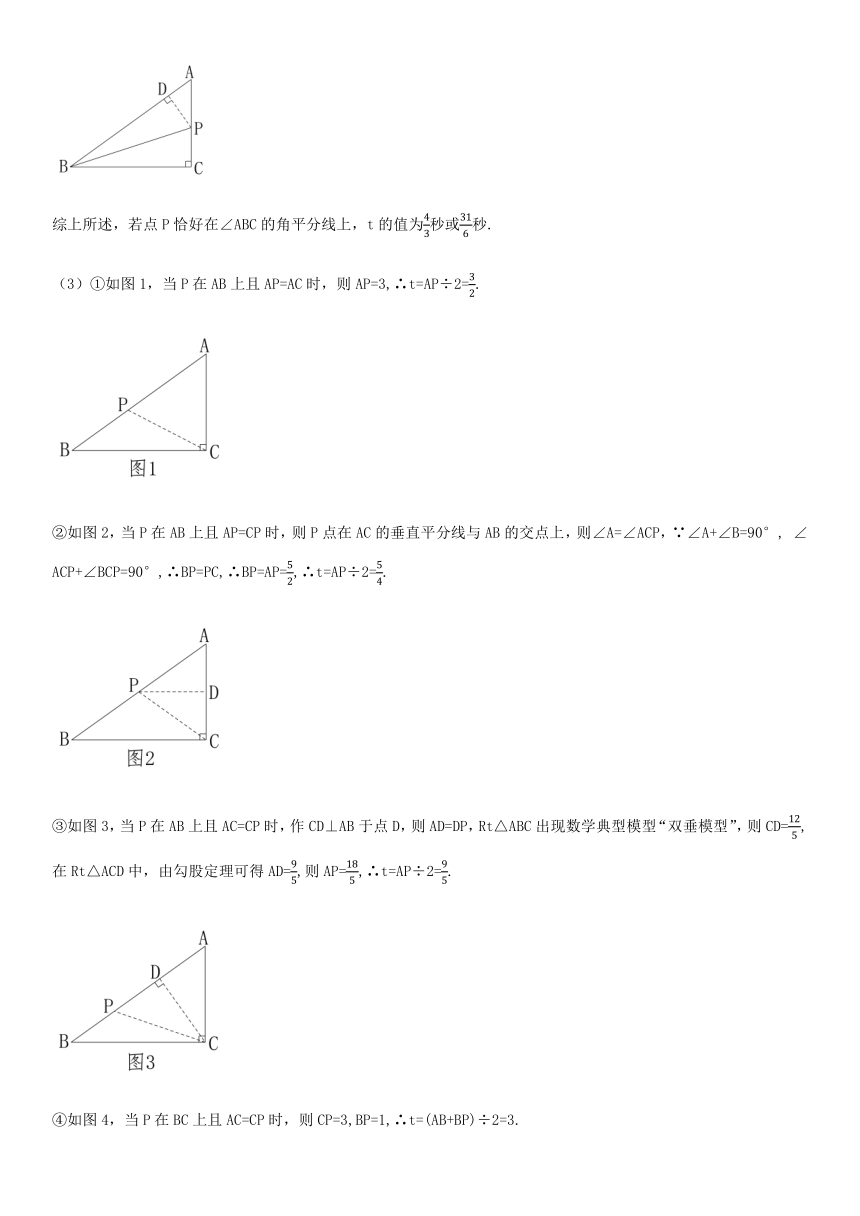
(2)若点P恰好在∠ABC的角平分线上,求此时t的值;
(3)在运动过程中,当t为何值时,△ACP为等腰三角形(直接写出答案)
解析:(1)由AB=5cm,BC=4cm及勾股定理可得AC=3cm;
(2)
①当P与B重合时,P恰好在∠ABC的角平分线上,t=AB÷2=52.
②过P作PD⊥AB于点D,由角平分线性质可得BD=BC=4,CP=DP,则AD=AB-BD=1,设CP=DP=x,则AP=3-x,在Rt△ADP中,由勾股定理可得x2+12=(3-x)2,解得x=43,即CP=43,则t=(AB+BC+CP)÷2=(5+4+43)÷2=316.
综上所述,若点P恰好在∠ABC的角平分线上,t的值为43秒或316秒.
(3)①如图1,当P在AB上且AP=AC时,则AP=3,∴t=AP÷2=32.
②如图2,当P在AB上且AP=CP时,则P点在AC的垂直平分线与AB的交点上,则∠A=∠ACP,∵∠A+∠B=90°, ∠ACP+∠BCP=90°,∴BP=PC,∴BP=AP=52,∴t=AP÷2=54.
③如图3,当P在AB上且AC=CP时,作CD⊥AB于点D,则AD=DP,Rt△ABC出现数学典型模型“双垂模型”,则CD=125,在Rt△ACD中,由勾股定理可得AD=95,则AP=185,∴t=AP÷2=95.
④如图4,当P在BC上且AC=CP时,则CP=3,BP=1,∴t=(AB+BP)÷2=3.
综上所述,当t等于32秒、54秒、95秒或3秒时,△ACP为等腰三角形
例3.如图1,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10,点D为y轴上一点,坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC--CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图2,把长方形沿OP折叠,点B的对应点B`恰好落在AC边上,求点P的坐标;
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由。
解析:(1)由C(6,10),D(0,2)可得yBD=43x+2
(2)①当点P在线段AC上时,OD=2,高为6,则S=6;
当点P在线段BC上时,OD=2,高为6+10-t=16-t,S=12×2×16-t=-t+16
∴△OPD的面积S关于t的函数解析式是S=6 S=-t+16
②设P(m,10),则PB=PB`=m,如图2,∵OB`=OB=10,OA=6,∴AB`=OB`2-OA2=8,∴B`C=10-8=2,∵PC=6-m,
∴22+(6-m)2=m2,解得m=103,所以此时P点的坐标为(103,10)
(3)存在,理由是:若△BDP为等腰三角形,分三种情况考虑:如图3
①当BD=BP1=OB-OD=10-2=8,在Rt△BCP1中,BP1=8,BC=6,根据勾股定理得:CP1=82-62=27,∴AP1=10-27,即P1(6,10-27);
②当BP2=DP2时,此时P2(6,6);
③当DB=DP3=8时,在Rt△DEP3中,DE=6, 根据勾股定理得:EP3=82-62=27,∴AP3=AE+EP3=2+27,即P3(6,2+27);
综上所述,满足题意的P点坐标为(6,10-27)、(6,6)或(6,2+27);
例4.如图,在平面直角坐标系xOy中,O为坐标原点,直线y=125x+12与x轴交于点A,与y轴交于点B,若点C在坐标轴上,且△ABC是以∠ABC为顶角的等腰三角形,则点C的坐标为 .
【分析】根据题意画出直线AB,根据勾股定理求出AB的长,再根据AB=BC即可得出结论.
【解答】∵直线y=125x+12与x轴交于点A,与y轴交于点B,
∴点A、点B的坐标分别为(﹣5,0)、(0,12),
∴AB=52+122=13.
∴C(5,0)或(0,﹣1)或(0,25).
例5.已知,如图,∠A=90°,BC//AD,AB=6cm,点P从A出发沿射线AD运动,速度是每秒1cm,点R从点B出发沿射线BC运动,速度是每秒2cm,点Q在点P的右侧,且PQ=10cm,时间为t秒.
(1)求△PQR的面积;
(2)当t=1秒时,求PR的长;
(3)当t为何值时,△PQR是等腰三角形
解析:
(1)求△PQR的面积,先确定面积方法----公式法,再确定公式中各量的数值:底PQ=10cm,高AB=6cm,∴S?PQR=12×10×6=30cm2;
(2)求线段PR的长,首选勾股定理,先明确直角三角形,图中PR不处于直角三角形中,故作垂线构造直角三角形,所以作PM⊥BC于点M,由题可知,当t=1秒时,AP=BM=1cm,BR=2cm,则RM=BR-BM=2-1=1cm,RM=BA=6cm,在Rt△PRM中,PR=MR2+PM2=62+12=37cm;
(3)方法一:“两圆一线”(注意:线段PQ是运动的,且BP>AP)
①如图2-1,以点P为圆心,已知长PQ为半径画圆,交BC交于点R1,作R1M⊥AD于点M,(另一交点在点P的左上方,由于BP>AP,舍去),在Rt△PR1M中,∵MR1=6,PR1=PQ=10,由勾股定理可得MP=8,由题可知:AP=t,BR1=AM=2t,∴2t=t+8,∴t=8;
②如图2-2,以点Q为圆心,已知长PQ为半径画圆,交BC交于点R2、R3,如图2-2-1,作R2M⊥AD于点M,在Rt△R2MQ中,∵MR2=6,QR2=PQ=10,由勾股定理可得QM=8,∴PM=2,∴2t=t+2,∴t=2;如图2-2-2,作R3M⊥AD于点M,在Rt△R3MQ中,∵MR3=6,QR3=PQ=10,由勾股定理可得QM=8,∴PM=18,∴2t=t+18,∴t=18;
③如图2-3,作PQ的垂直平分线MR,交AD于点M,BC于点R4,∵△PQR4是等腰三角形,∴PM=MQ=5,∴2t=t+5,∴t=5;
∴综上所述,当t为2秒、5秒、8秒或12秒时,△PQR是等腰三角形.
方法二:三边两两相等分三种情形分别论证
①当PQ=PR时,解题步骤与方法一中的①相同;
②当PQ=QR时,解题步骤与方法一中的②相同;
③当PR=QR时,解题步骤与方法一中的③相同;
【方法梳理】
1.“两定一动”情形:“两圆一线”;
2.所有情形:分三边两两相等分别论证解答;
3.解题思维习惯:先分情况、再画图形、最后由易到难顺序依次解答;
【典型例题】
例1.如图,长方形OABC,O是原点,点A、C分别在坐标轴上,OA=BC=10,AB=OC=8,在OC边上取一点D,将长方形沿AD折叠,使点O落在BC边上的点E处,连接ED并延长交x轴于点F.
(1)直接写出A、B两点的坐标;
(2)求出线段OD的长和直线DE的解析式;DO=5,
(3)在x轴上是否存在一点P,使△ADP为以AD为腰的等腰三角形,若存在,求出P点坐标;若不存在,请说明理由;
(4)点Q由O点出发,以每秒2个单位长度沿OD向D点运动,到达D点时运动终止,设△QDF的面积为S,设Q运动的时间为t,求出S与t的函数关系式;
解析: (1)A(10,0),B(0,8)
(2)设OD=x,由题可知CD=8-x,DE=x,在Rt△ABE中,AE=OA=10,AB=8,由勾股定理可得BE=6,则CE=4,在Rt△CDE中,由CD2+CE2=DE2可得42+(8-x)2=x2,解得x=5,即OD=5,由D(0,5)、E(4,8)可得直线DE的解析式为y=34x+5.
(3)由于题目明确AD为腰,所以只需要画“两圆”。由(2)可知AD=55,
①以A为圆心,AD为半径画圆,与x轴有两个交点P1,P2,则AP=AD=55,则OP=10±55,
∴P点坐标为(10+55,0)或(10-55,0)
②以D为圆心,AD为半径画圆,与x轴有两个交点P3,P4(P4与点A重合,舍去),
连接DP3,由AD=DP3可得O P3=OA=10,∴P3 (-10,0)
综上所述,点P的坐标为(-10,0)、(10+55,0)或(10-55,0).
(4)由直线DE的解析式y=34x+5可得F点的坐标为(-203,0),由题可知DQ=5-2t,
∴S?QDF=12?DQ?OF=12×2035-2t=-203t+503
例2.如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒2cm的速度沿折线A-B-C-A运动,设运动时间为t秒(t>0),
(1)AC=_______cm;
(2)若点P恰好在∠ABC的角平分线上,求此时t的值;
(3)在运动过程中,当t为何值时,△ACP为等腰三角形(直接写出答案)
解析:(1)由AB=5cm,BC=4cm及勾股定理可得AC=3cm;
(2)
①当P与B重合时,P恰好在∠ABC的角平分线上,t=AB÷2=52.
②过P作PD⊥AB于点D,由角平分线性质可得BD=BC=4,CP=DP,则AD=AB-BD=1,设CP=DP=x,则AP=3-x,在Rt△ADP中,由勾股定理可得x2+12=(3-x)2,解得x=43,即CP=43,则t=(AB+BC+CP)÷2=(5+4+43)÷2=316.
综上所述,若点P恰好在∠ABC的角平分线上,t的值为43秒或316秒.
(3)①如图1,当P在AB上且AP=AC时,则AP=3,∴t=AP÷2=32.
②如图2,当P在AB上且AP=CP时,则P点在AC的垂直平分线与AB的交点上,则∠A=∠ACP,∵∠A+∠B=90°, ∠ACP+∠BCP=90°,∴BP=PC,∴BP=AP=52,∴t=AP÷2=54.
③如图3,当P在AB上且AC=CP时,作CD⊥AB于点D,则AD=DP,Rt△ABC出现数学典型模型“双垂模型”,则CD=125,在Rt△ACD中,由勾股定理可得AD=95,则AP=185,∴t=AP÷2=95.
④如图4,当P在BC上且AC=CP时,则CP=3,BP=1,∴t=(AB+BP)÷2=3.
综上所述,当t等于32秒、54秒、95秒或3秒时,△ACP为等腰三角形
例3.如图1,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10,点D为y轴上一点,坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC--CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图2,把长方形沿OP折叠,点B的对应点B`恰好落在AC边上,求点P的坐标;
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由。
解析:(1)由C(6,10),D(0,2)可得yBD=43x+2
(2)①当点P在线段AC上时,OD=2,高为6,则S=6;
当点P在线段BC上时,OD=2,高为6+10-t=16-t,S=12×2×16-t=-t+16
∴△OPD的面积S关于t的函数解析式是S=6 S=-t+16
②设P(m,10),则PB=PB`=m,如图2,∵OB`=OB=10,OA=6,∴AB`=OB`2-OA2=8,∴B`C=10-8=2,∵PC=6-m,
∴22+(6-m)2=m2,解得m=103,所以此时P点的坐标为(103,10)
(3)存在,理由是:若△BDP为等腰三角形,分三种情况考虑:如图3
①当BD=BP1=OB-OD=10-2=8,在Rt△BCP1中,BP1=8,BC=6,根据勾股定理得:CP1=82-62=27,∴AP1=10-27,即P1(6,10-27);
②当BP2=DP2时,此时P2(6,6);
③当DB=DP3=8时,在Rt△DEP3中,DE=6, 根据勾股定理得:EP3=82-62=27,∴AP3=AE+EP3=2+27,即P3(6,2+27);
综上所述,满足题意的P点坐标为(6,10-27)、(6,6)或(6,2+27);
例4.如图,在平面直角坐标系xOy中,O为坐标原点,直线y=125x+12与x轴交于点A,与y轴交于点B,若点C在坐标轴上,且△ABC是以∠ABC为顶角的等腰三角形,则点C的坐标为 .
【分析】根据题意画出直线AB,根据勾股定理求出AB的长,再根据AB=BC即可得出结论.
【解答】∵直线y=125x+12与x轴交于点A,与y轴交于点B,
∴点A、点B的坐标分别为(﹣5,0)、(0,12),
∴AB=52+122=13.
∴C(5,0)或(0,﹣1)或(0,25).
例5.已知,如图,∠A=90°,BC//AD,AB=6cm,点P从A出发沿射线AD运动,速度是每秒1cm,点R从点B出发沿射线BC运动,速度是每秒2cm,点Q在点P的右侧,且PQ=10cm,时间为t秒.
(1)求△PQR的面积;
(2)当t=1秒时,求PR的长;
(3)当t为何值时,△PQR是等腰三角形
解析:
(1)求△PQR的面积,先确定面积方法----公式法,再确定公式中各量的数值:底PQ=10cm,高AB=6cm,∴S?PQR=12×10×6=30cm2;
(2)求线段PR的长,首选勾股定理,先明确直角三角形,图中PR不处于直角三角形中,故作垂线构造直角三角形,所以作PM⊥BC于点M,由题可知,当t=1秒时,AP=BM=1cm,BR=2cm,则RM=BR-BM=2-1=1cm,RM=BA=6cm,在Rt△PRM中,PR=MR2+PM2=62+12=37cm;
(3)方法一:“两圆一线”(注意:线段PQ是运动的,且BP>AP)
①如图2-1,以点P为圆心,已知长PQ为半径画圆,交BC交于点R1,作R1M⊥AD于点M,(另一交点在点P的左上方,由于BP>AP,舍去),在Rt△PR1M中,∵MR1=6,PR1=PQ=10,由勾股定理可得MP=8,由题可知:AP=t,BR1=AM=2t,∴2t=t+8,∴t=8;
②如图2-2,以点Q为圆心,已知长PQ为半径画圆,交BC交于点R2、R3,如图2-2-1,作R2M⊥AD于点M,在Rt△R2MQ中,∵MR2=6,QR2=PQ=10,由勾股定理可得QM=8,∴PM=2,∴2t=t+2,∴t=2;如图2-2-2,作R3M⊥AD于点M,在Rt△R3MQ中,∵MR3=6,QR3=PQ=10,由勾股定理可得QM=8,∴PM=18,∴2t=t+18,∴t=18;
③如图2-3,作PQ的垂直平分线MR,交AD于点M,BC于点R4,∵△PQR4是等腰三角形,∴PM=MQ=5,∴2t=t+5,∴t=5;
∴综上所述,当t为2秒、5秒、8秒或12秒时,△PQR是等腰三角形.
方法二:三边两两相等分三种情形分别论证
①当PQ=PR时,解题步骤与方法一中的①相同;
②当PQ=QR时,解题步骤与方法一中的②相同;
③当PR=QR时,解题步骤与方法一中的③相同;
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
