北师大版八年级数学下册1.2有关等腰三角形题型学案(含答案)
文档属性
| 名称 | 北师大版八年级数学下册1.2有关等腰三角形题型学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 148.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览



文档简介
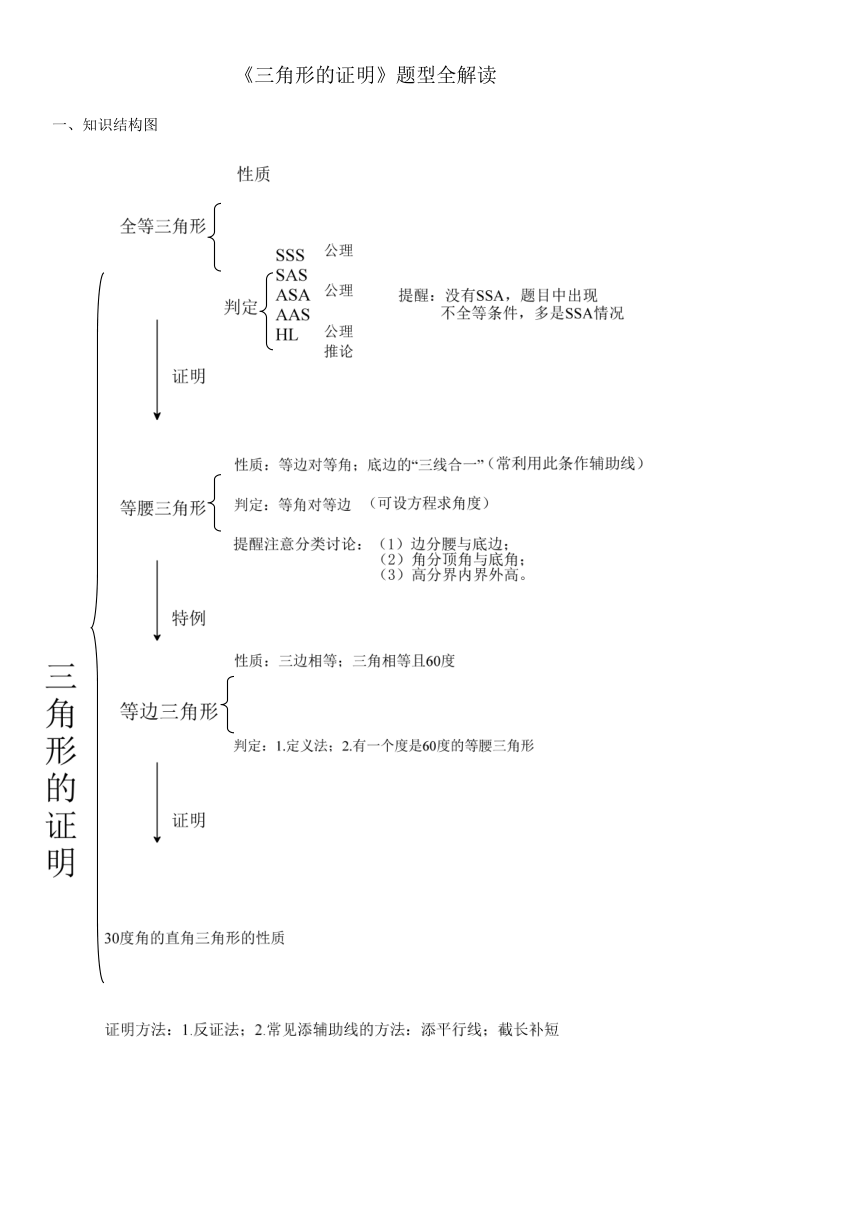
1165860012674600《三角形的证明》题型全解读
一、知识结构图
14859000
13716009906045720099060
2286000018288000
29432253619522860000342900018288000137160099060
2286000180975228600008001000
9144000
365760099060148590099060
2628900990601485900990601371600045720099060
148590099060
8001000
9144000
-180975102235148590046355
1485900045720099060
148590099060
8001000
9144000
3429000
34290090805
41148009906014859000
42291000148590004572000
14859000
13716000
42291009906012573000137160016573545720082550
4229100819154572001083310137160089154014859001485900148590012680951485900990600148590059436013716003962401371600198120
60579000
61722000
411480099060
423164097155
《三角形的证明》题型解读1 有关等腰三角形题型
【知识梳理】
1.主要性质
2.两个重点:①“三线合一”;②分类讨论;
【典型例题】
例1.如图,在△ABC中,AB=AC,∠A=36°,D、E两点分别在AC、BC上,BD平分∠ABC,DE∥AB。图中的等腰三角形共有( )
A.3个 B.4个 C.5个 D.6个
解析:△ABC、△ABD、△DEB、△BDC、△DEC是等腰三角形;
266700292735例2.如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数是________
解析:由等腰三角形性质及三角形内角和公式及外角定理解答,可得∠C的度数是35°
例3.如图,AD是△ABC的角平分线,DE⊥AC于E,BF//AC交ED的延长线于点F,BC恰好平分∠ABF,AE=2BF,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,
2105025108585其中正确的结论共有( )个
A. 4 B. 3 C. 2 D. 1
5751195802005解析:由“角平分线+平行线=等腰△”即BC恰好平分∠ABF,BF//AC可得△ABC是等腰三角形,AB=AC,∵AD是△ABC的角平分线,由等腰三角形性质“三线合一”可得AD⊥BC,BD=CD,②③正确;则由ASA易证△BDF≌△CDE,可得BF=CE,DE=DF,①正确;由AE=2BF,CE=BF可得AC=3BF,④正确;故选A
例4.如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.
若∠E=35°,则∠BAC的度数为______40°
解析:由AE//BD可得∠E=∠DBC=35°,由BD是角平分线可得∠ABC=70°=∠C,由三角形内角和公式可得∠BAC=40°.
例5.一个等腰三角形的一个角为50?,则它的顶角的度数是_______
解析:考查等腰三角形的分类讨论。
①当顶角为50?时,它的顶角的度数是50?;
②当底角为50?时,它的顶角的度数是80?;∴它的顶角的度数是50?或80?.
例6. 等腰三角形的一个外角是60°,则它顶角的度数是_________120°
①当60?是顶角的外角时,它的顶角的度数是120?;
②当50?是底角的外角时,它的一个底角的度数是120?,不符合三角形内角和公式,舍去;
∴它的顶角的度数是120?.
例7.等腰三角形一腰上的高与另一腰的夹角的度数是20°,则顶角的度数是____110°或70°_____
解析:①当等腰三角形是锐角三角形,高为界内高时,顶角的度数是90°-20°=70°;
②当等腰三角形是钝角三角形,高为界外高时,顶角的度数是90°+20°=110°;
例8.等腰三角形一腰长为5,一边上的高为3,则底边长________
解析:如图分类讨论分别计算,可得底边长为8、10或310
center8382015621008191551435076200
例9.某等腰三角形两条边长分别是4和6,则它的周长是__________14、16
解析:①当底是4腰是6时,周长为16;②当底是6腰是4时,周长为14;
∴它的周长是14或16
5095875268605例10.若实数m、n满足等式|m﹣2|+n-4=0,且m、n恰好是等腰△ABC的两条边边长,则△ABC的周长是___
6170930115570
6047105-132080
解析:由题可得m=2,n=4,由三角形三边关系可知4为腰2为底,故周长是10.
例11如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F。
(1)求证:AE=AE;
(2)求证:△BFC是等腰三角形。
解析:(1)利用“∠A=∠A,∠AEC=∠ADB=90°,AB=AC”证△ABD≌△ACE可得AE=AD;
(2)由△ABD≌△ACE可得∠ABD=∠ACE,由∠ABC=∠ACB可得∠FBC=∠FCB,∴BF=CF,∴△FBC是等腰三角形
4305935289560例12.如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B`的位置,AB`与CD交于点E,已知AB=8,
AD=4,请完成下列问题:
(1)求证:△ACE是等腰三角形;
(2)求重叠部分(△ACE)的面积;
(3)P为线段AC上的任意一点,试求PE+PC的最小值;
解析:
(1)数学典型模型:“角平分线+平行线=等腰三角形”。由折叠可得∠EAC=∠BAC,由矩形可得DC//AB,∴∠EAC=∠BAC=∠ECA,∴△ACE是等腰三角形;
(2)勾股定理的典型解题思路:“折叠性质+方程思想+勾股定理”,设EC=x,则AE=x,DE=8-x,在Rt△ADE中,由勾股定理可得:42+(8-x)2=x2,解得x=5,∴S?AEC=12?EC?AD=12×5×4=10.
(3)数学典型题型:“将军饮马问题”,不过是最基础最简单的一类---当P、E、C成一直线时PE+PC最小。
△PEC中,由三边关系可得:PE+PC>EC,当P点在C点时,PE+PC=EC,有最小值,最小值是EC=5.
例13.如图1.△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC作等腰Rt△ABE
和等腰Rt△ACF,过点E,F作射线GA的垂线,垂足分别为P,Q.
(1)求证:△EPA≌△AGB:
(2)试探究EP与FQ之间的数量关系,并证明你的结论;
(3)如图2.若连接EF交GA的延长线于H,由(2)中的结论你能判断EH与FH的大小关系吗?并说明理由:
(4)在(3)的条件下,若BC=10,AG=12.请直接写出S△AEF= .
【分析】
(1)根据等腰Rt△ABE的性质,求出∠EPA=∠EAB=∠AGB=90°,∠PEA=∠BAG,根据AAS推出△EPA≌△AGB.
(2)根据全等三角形的性质推出EP=AG,同理可得△FQA≌△AGC,即可得出AG=FQ,最后等量代换即可得出答案.
(3)求出∠EPH=∠FQH=90°,根据AAS推出△EPH≌△FQH,即可得出EH与FH的大小关系.
(4)根据全等三角形△EPH≌△FQH,△EPA≌△AGB,△FQA≌△AGC,推出S△FQA=S△AGC,S△FQH=S△EPH,S△EPA=S△AGB,即可求出S△AEF=S△ABC,根据三角形面积公式求出即可.
【解答】(1)如图1,∵∠EAB=90°,EP⊥AG,AG⊥BC,∴∠EPA=∠EAB=∠AGB=90°,
∴∠PEA+∠EAP=90°,∠EAP+∠BAG=90°,∴∠PEA=∠BAG,
在△EPA和△AGB中,
,
∴△EPA≌△AGB(AAS),
(2)结论:EP=FQ,
证明:由(1)可得,△EPA≌△AGB,∴EP=AG,同理可得,△FQA≌△AGC,
∴AG=FQ,∴EP=FQ;
(3)结论:EH=FH,
理由:如图,∵EP⊥AG,FQ⊥AG,∴∠EPH=∠FQH=90°,
在△EPH和△FQH中,
,
∴△EPH≌△FQH(AAS),
∴EH=FH.
(4)∵△EPH≌△FQH,△EPA≌△AGB,△FQA≌△AGC,
∴S△FQA=S△AGC,S△FQH=S△EPH,S△EPA=S△AGB,
∴S△AEF=S△EPA+S△FQA=S△AGB+S△AGC=S△ABC=×BC×AG=×10×12=60
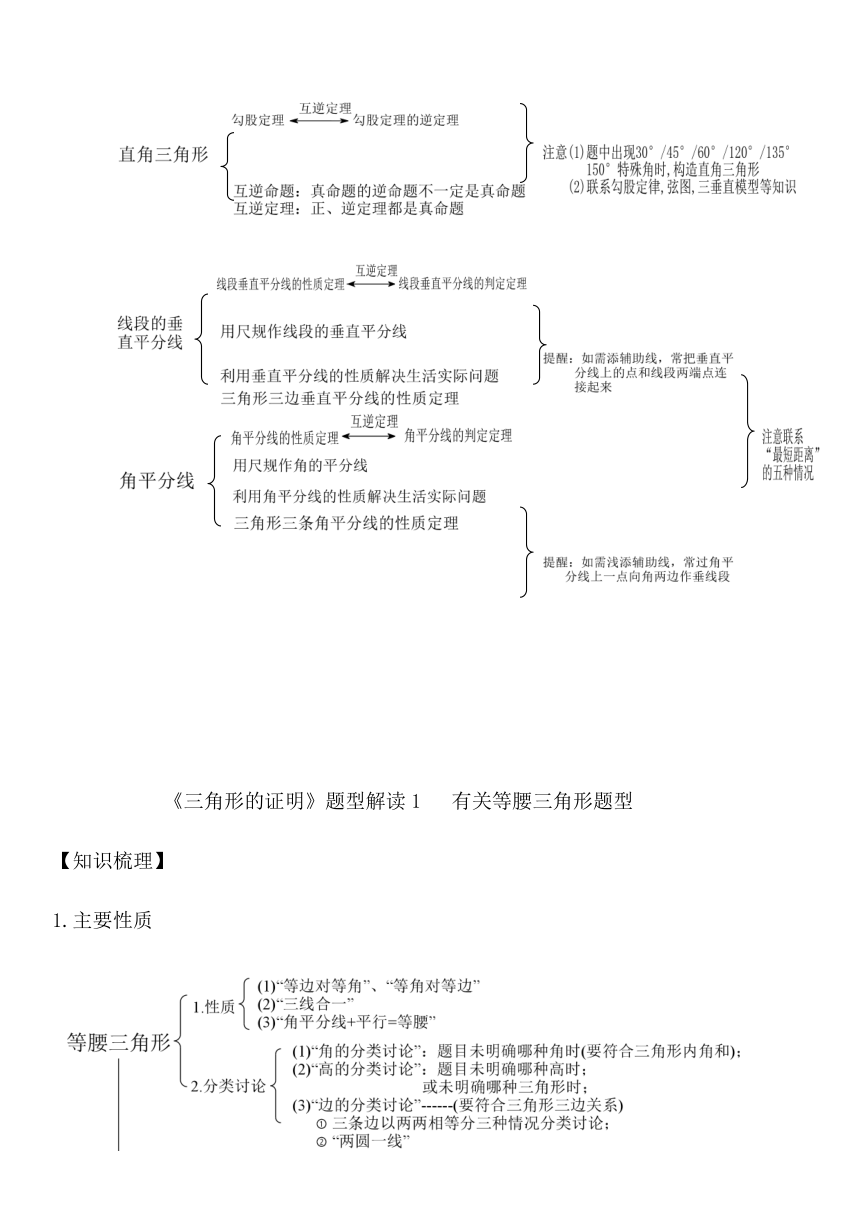
一、知识结构图
14859000
13716009906045720099060
2286000018288000
29432253619522860000342900018288000137160099060
2286000180975228600008001000
9144000
365760099060148590099060
2628900990601485900990601371600045720099060
148590099060
8001000
9144000
-180975102235148590046355
1485900045720099060
148590099060
8001000
9144000
3429000
34290090805
41148009906014859000
42291000148590004572000
14859000
13716000
42291009906012573000137160016573545720082550
4229100819154572001083310137160089154014859001485900148590012680951485900990600148590059436013716003962401371600198120
60579000
61722000
411480099060
423164097155
《三角形的证明》题型解读1 有关等腰三角形题型
【知识梳理】
1.主要性质
2.两个重点:①“三线合一”;②分类讨论;
【典型例题】
例1.如图,在△ABC中,AB=AC,∠A=36°,D、E两点分别在AC、BC上,BD平分∠ABC,DE∥AB。图中的等腰三角形共有( )
A.3个 B.4个 C.5个 D.6个
解析:△ABC、△ABD、△DEB、△BDC、△DEC是等腰三角形;
266700292735例2.如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数是________
解析:由等腰三角形性质及三角形内角和公式及外角定理解答,可得∠C的度数是35°
例3.如图,AD是△ABC的角平分线,DE⊥AC于E,BF//AC交ED的延长线于点F,BC恰好平分∠ABF,AE=2BF,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,
2105025108585其中正确的结论共有( )个
A. 4 B. 3 C. 2 D. 1
5751195802005解析:由“角平分线+平行线=等腰△”即BC恰好平分∠ABF,BF//AC可得△ABC是等腰三角形,AB=AC,∵AD是△ABC的角平分线,由等腰三角形性质“三线合一”可得AD⊥BC,BD=CD,②③正确;则由ASA易证△BDF≌△CDE,可得BF=CE,DE=DF,①正确;由AE=2BF,CE=BF可得AC=3BF,④正确;故选A
例4.如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.
若∠E=35°,则∠BAC的度数为______40°
解析:由AE//BD可得∠E=∠DBC=35°,由BD是角平分线可得∠ABC=70°=∠C,由三角形内角和公式可得∠BAC=40°.
例5.一个等腰三角形的一个角为50?,则它的顶角的度数是_______
解析:考查等腰三角形的分类讨论。
①当顶角为50?时,它的顶角的度数是50?;
②当底角为50?时,它的顶角的度数是80?;∴它的顶角的度数是50?或80?.
例6. 等腰三角形的一个外角是60°,则它顶角的度数是_________120°
①当60?是顶角的外角时,它的顶角的度数是120?;
②当50?是底角的外角时,它的一个底角的度数是120?,不符合三角形内角和公式,舍去;
∴它的顶角的度数是120?.
例7.等腰三角形一腰上的高与另一腰的夹角的度数是20°,则顶角的度数是____110°或70°_____
解析:①当等腰三角形是锐角三角形,高为界内高时,顶角的度数是90°-20°=70°;
②当等腰三角形是钝角三角形,高为界外高时,顶角的度数是90°+20°=110°;
例8.等腰三角形一腰长为5,一边上的高为3,则底边长________
解析:如图分类讨论分别计算,可得底边长为8、10或310
center8382015621008191551435076200
例9.某等腰三角形两条边长分别是4和6,则它的周长是__________14、16
解析:①当底是4腰是6时,周长为16;②当底是6腰是4时,周长为14;
∴它的周长是14或16
5095875268605例10.若实数m、n满足等式|m﹣2|+n-4=0,且m、n恰好是等腰△ABC的两条边边长,则△ABC的周长是___
6170930115570
6047105-132080
解析:由题可得m=2,n=4,由三角形三边关系可知4为腰2为底,故周长是10.
例11如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F。
(1)求证:AE=AE;
(2)求证:△BFC是等腰三角形。
解析:(1)利用“∠A=∠A,∠AEC=∠ADB=90°,AB=AC”证△ABD≌△ACE可得AE=AD;
(2)由△ABD≌△ACE可得∠ABD=∠ACE,由∠ABC=∠ACB可得∠FBC=∠FCB,∴BF=CF,∴△FBC是等腰三角形
4305935289560例12.如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B`的位置,AB`与CD交于点E,已知AB=8,
AD=4,请完成下列问题:
(1)求证:△ACE是等腰三角形;
(2)求重叠部分(△ACE)的面积;
(3)P为线段AC上的任意一点,试求PE+PC的最小值;
解析:
(1)数学典型模型:“角平分线+平行线=等腰三角形”。由折叠可得∠EAC=∠BAC,由矩形可得DC//AB,∴∠EAC=∠BAC=∠ECA,∴△ACE是等腰三角形;
(2)勾股定理的典型解题思路:“折叠性质+方程思想+勾股定理”,设EC=x,则AE=x,DE=8-x,在Rt△ADE中,由勾股定理可得:42+(8-x)2=x2,解得x=5,∴S?AEC=12?EC?AD=12×5×4=10.
(3)数学典型题型:“将军饮马问题”,不过是最基础最简单的一类---当P、E、C成一直线时PE+PC最小。
△PEC中,由三边关系可得:PE+PC>EC,当P点在C点时,PE+PC=EC,有最小值,最小值是EC=5.
例13.如图1.△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC作等腰Rt△ABE
和等腰Rt△ACF,过点E,F作射线GA的垂线,垂足分别为P,Q.
(1)求证:△EPA≌△AGB:
(2)试探究EP与FQ之间的数量关系,并证明你的结论;
(3)如图2.若连接EF交GA的延长线于H,由(2)中的结论你能判断EH与FH的大小关系吗?并说明理由:
(4)在(3)的条件下,若BC=10,AG=12.请直接写出S△AEF= .
【分析】
(1)根据等腰Rt△ABE的性质,求出∠EPA=∠EAB=∠AGB=90°,∠PEA=∠BAG,根据AAS推出△EPA≌△AGB.
(2)根据全等三角形的性质推出EP=AG,同理可得△FQA≌△AGC,即可得出AG=FQ,最后等量代换即可得出答案.
(3)求出∠EPH=∠FQH=90°,根据AAS推出△EPH≌△FQH,即可得出EH与FH的大小关系.
(4)根据全等三角形△EPH≌△FQH,△EPA≌△AGB,△FQA≌△AGC,推出S△FQA=S△AGC,S△FQH=S△EPH,S△EPA=S△AGB,即可求出S△AEF=S△ABC,根据三角形面积公式求出即可.
【解答】(1)如图1,∵∠EAB=90°,EP⊥AG,AG⊥BC,∴∠EPA=∠EAB=∠AGB=90°,
∴∠PEA+∠EAP=90°,∠EAP+∠BAG=90°,∴∠PEA=∠BAG,
在△EPA和△AGB中,
,
∴△EPA≌△AGB(AAS),
(2)结论:EP=FQ,
证明:由(1)可得,△EPA≌△AGB,∴EP=AG,同理可得,△FQA≌△AGC,
∴AG=FQ,∴EP=FQ;
(3)结论:EH=FH,
理由:如图,∵EP⊥AG,FQ⊥AG,∴∠EPH=∠FQH=90°,
在△EPH和△FQH中,
,
∴△EPH≌△FQH(AAS),
∴EH=FH.
(4)∵△EPH≌△FQH,△EPA≌△AGB,△FQA≌△AGC,
∴S△FQA=S△AGC,S△FQH=S△EPH,S△EPA=S△AGB,
∴S△AEF=S△EPA+S△FQA=S△AGB+S△AGC=S△ABC=×BC×AG=×10×12=60
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
