人教版九年级上册数学第二十五章概率章末 复习课件(共40页PPT)
文档属性
| 名称 | 人教版九年级上册数学第二十五章概率章末 复习课件(共40页PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 17:36:06 | ||
图片预览








文档简介
(共40张PPT)
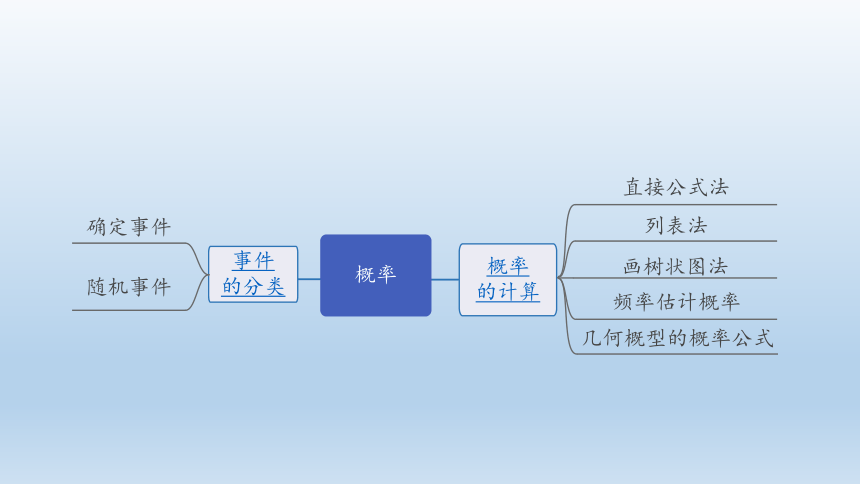
事件
的分类
确定事件
随机事件
概率
的计算
直接公式法
列表法
画树状图法
频率估计概率
几何概型的概率公式
概率
【课标要求】
◎能通过列表、画树状图等方法列出简单随机事件所有可能的结果,以及指定事件发生的所有可能的结果,了解事件的概率;
◎知道通过大量的重复试验,可以用频率来估计概率.
【对接教材】冀教:九下第三十一章P60-P80;
人教:九上第二十五章P126-P153;
北师:七下第六章P135-P159,九上第三章P59-P74.
考点
1
事件的分类
确定事件
必然事件:在一定条件下,必然会发生的事件,概率P=________
不可能事件:在一定条件下,不可能发生的事件,概率P=________
随机事件
在一定条件下,可能发生也可能不发生的事件,概率在0~1之间
1
0
考点
2
概率的计算
直接公式法
如果一个试验有n种可能的结果,事件A包含其中的m种结果,那么事件
A发生的概率为P(A)=________
列表法
如果一次试验涉及两个因素,并且只有有限个等可能的结果,结果数目较多时,通常采用列表法求事件发生的概率
画树状图法
当一次试验涉及三个或更多的因素时,通常采用画树状图法来求事件发生的概率
频率估计概率
一般地,做n次重复试验,如果事件A发生了m次,比值稳定于某个常数p.那么事件A发生的概率:P(A)=p
几何概型的概率公式
一、概率的计算
例 在一个不透明口袋中有四个小球,分别标有数字-3,0,1,2,每个小球除数字不同外其余均相同,每次试验先摇匀.
(1)从中摸出一个球,数字为3是________事件,从中摸出3个球,至少有1个正数是________事件,从中摸出2个球,有一个数字是0是______事件;
(2)从中随机取一个小球,则取出的小球上的数字为负数的概率为________;
(3)若再向口袋中放入n个标有负数的小球摇匀,再从不透明口袋中取一个小球,摸到数字为正整数的概率为
,则加入的小球个数n为________;
随机
不可能
必然
4
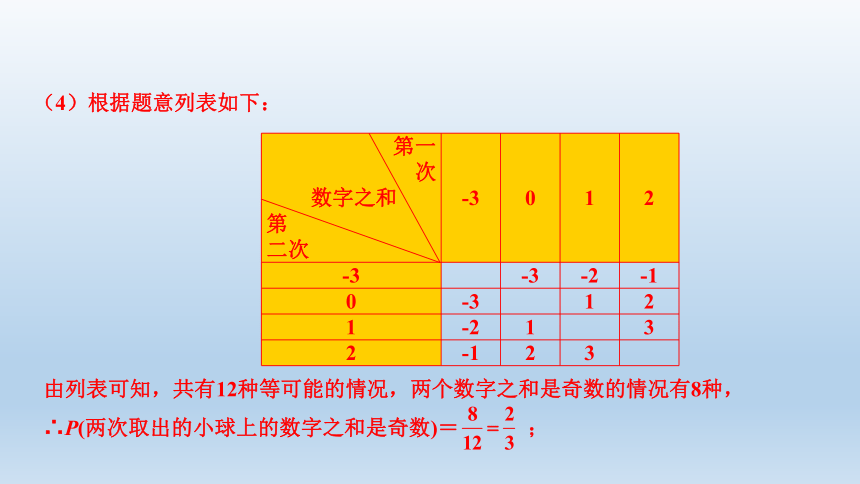
(4)先从口袋中随机取一个小球,记下小球上的数字,再从剩下的小球中随机取一个小球,再记下小球上的数字.求两次取出的小球上的数字之和是奇数的概率;
(4)根据题意列表如下:
第一
次
数字之和
第
二次
-3
0
1
2
-3
-3
-2
-1
0
-3
1
2
1
-2
1
3
2
-1
2
3
由列表可知,共有12种等可能的情况,两个数字之和是奇数的情况有8种,
∴P(两次取出的小球上的数字之和是奇数)=
;
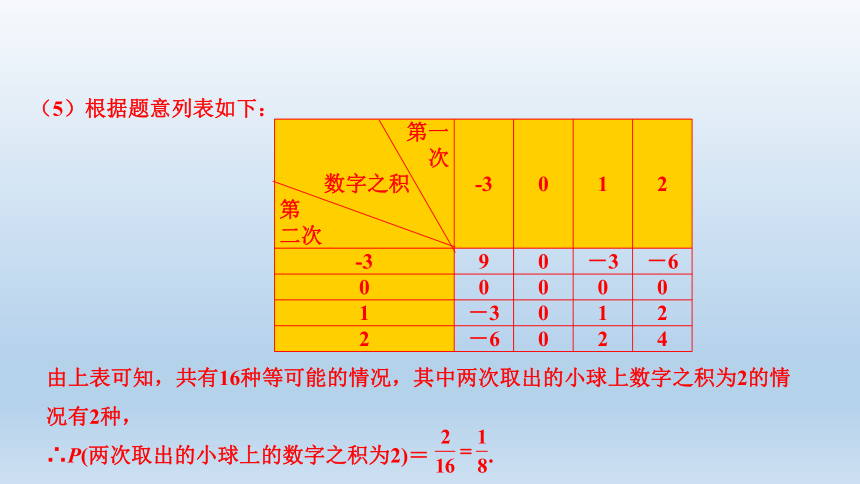
(5)先从口袋中随机取一个小球,记下小球上的数字,放回搅拌均匀后,再从中随机取一个小球,再记下小球上的数字,求两次取出的小球上的数字之积为2的概率;
(5)根据题意列表如下:
由上表可知,共有16种等可能的情况,其中两次取出的小球上数字之积为2的情况有2种,
∴P(两次取出的小球上的数字之积为2)=
.
第一
次
数字之积
第
二次
-3
0
1
2
-3
9
0
-3
-6
0
0
0
0
0
1
-3
0
1
2
2
-6
0
2
4
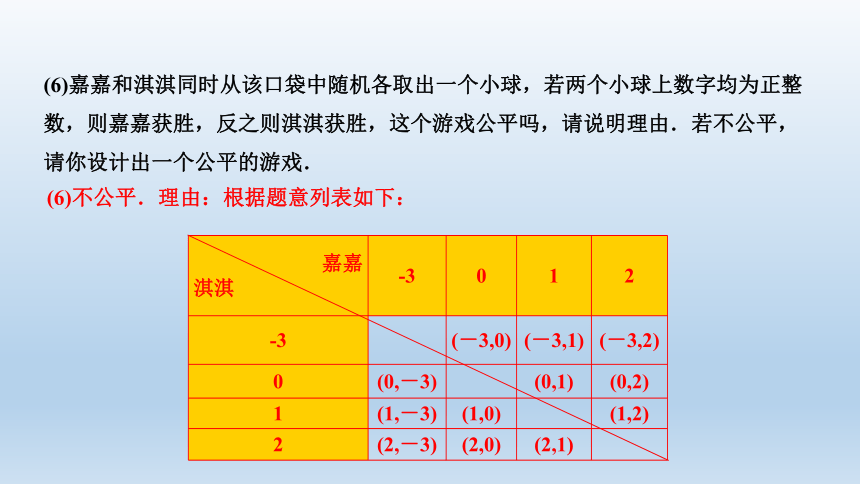
(6)嘉嘉和淇淇同时从该口袋中随机各取出一个小球,若两个小球上数字均为正整数,则嘉嘉获胜,反之则淇淇获胜,这个游戏公平吗,请说明理由.若不公平,请你设计出一个公平的游戏.
(6)不公平.理由:根据题意列表如下:
嘉嘉
淇淇
-3
0
1
2
-3
(-3,0)
(-3,1)
(-3,2)
0
(0,-3)
(0,1)
(0,2)
1
(1,-3)
(1,0)
(1,2)
2
(2,-3)
(2,0)
(2,1)
由列表可知,共有12种等可能的情况,
其中两个小球上数字均为正整数的情况有2种,
∴P(嘉嘉获胜)=
,
P(淇淇获胜)=
.
∵P(嘉嘉获胜)≠P(淇淇获胜),
∴不公平.
公平的游戏可以设计为:从该口袋中随机取两个小球,这两个小球上数字之和大于0,则嘉嘉获胜,小于0,则淇淇获胜.(答案不唯一)
练习1 (2020泰州)如图,电路图上有4个开关A、B、C、D和1个小灯泡,同时闭合开关A、B或同时闭合开关C、D都可以使小灯泡发光.下列操作中,“小灯泡发光”这个事件是随机事件的是( )
A.
只闭合1个开关 B.
只闭合2个开关
C.
只闭合3个开关
D.
闭合4个开关
练习1题图
B
练习2 如图,一个圆形转盘被等分为八个扇形区域,上面分别标有数字1、2、3、5,转盘指针的位置固定,转动转盘后任其自由停止.转动转盘一次,当转盘停止时,记指针指向标有“3”所在区域的概率为P(3),指针指向标有“5”所在区域的概率为P(5),则P(3)______P(5).(填“>”“
=”或“<”
)
练习2题图
>
二、统计与概率结合
练习3 (2020河北大模考)在抗击新型冠状病毒肺炎战役中,某市党员积极响应国家号召参加志愿者活动,为人民服务,现随机抽查部分党员一个月来参加志愿者活动的次数,并绘制成如下尚不完整的条形统计图(图①)和扇形统计图(图②).
图①
图②
练习3题图
(1)“4次”所在扇形的圆心角度数是________,请补全条形统计图;
72°
(1)补全条形统计图如解图所示;
练习3题解图
(2)∵随机抽查的党员人数为10÷20%=50(人),其中参加志愿者活动次数不少于3次的有14+10+8=32(人),
∴P(该党员一个月来参加志愿者活动次数不少于3次)=
;
(2)若从抽查的党员中随机选择一位接受媒体的采访,求该党员一个月来参加志愿者活动次数不少于3次的概率;
(3)设随机抽查的党员一个月来参加志愿者活动次数的中位数为a,若去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为b,当b>a时,求最少去掉了几名党员参加志愿者活动的次数.
(3)将参加次数按由小到大进行排列,可得中位数为第25、26个数的平均数,由题意得a=
=3,
∵去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为b,且b>a,
∴b=4或5.当b=4时,最少需去掉10名党员参加志愿者活动的次数,即去掉5个参加志愿者活动次数为2次的和5个参加志愿者活动次数为3次的;
当b=5时,最少需去掉17名党员参加志愿者活动的次数,
即去掉7个参加活动为2次的,7个参加活动为3次的,3个参加活动为4次的,
∵10<17,
∴b=4.
这时最少去掉了10名党员这一个月来参加志愿者活动的次数,即去掉5个参加志愿者活动次数为2次的和5个参加志愿者活动次数为3次的.
类型一 以数字为背景的概率计算(10年3考
)
1.
(2015河北13题2分)将一质地均匀的正方体骰子抛掷一次,观察向上一面的点数,与点数3相差2的概率是( )
A.
B.
C.
D.
B
2.
(2016河北23题9分)如图①,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.
如图②,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;…
设游戏者从圈A起跳.
(1)嘉嘉随机掷一次骰子,求落回到圈A的概率P1;
第2题图
解:(1)∵掷一次质地均匀的正四面体骰子有4种等可能结果,只有掷得4时,才会落回到圈A,
∴P1(落回到圈A)=
;
(2)淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2,并指出她与嘉嘉落回到圈A的可能性一样吗?
第2题图
(2)列表如下:
第一次
第二次
1
2
3
4
1
(1,1)
(2,1)
(3,1)
(4,1)
2
(1,2)
(2,2)
(3,2)
(4,2)
3
(1,3)
(2,3)
(3,3)
(4,3)
4
(1,4)
(2,4)
(3,4)
(4,4)
∴P2(最后落回到圈A)=
,
∵P1=P2=
,
∴淇淇与嘉嘉落回到圈A的可能性一样.
由列表可知,共有16种等可能的结果,当两次掷得的数字和为4的倍数,即(1,3),(2,2),(3,1),(4,4)时,才可落回到圈A,共有4种,
类型二 与统计结合的概率计算(10年3考
)
3.
(2017河北21题9分)编号为1~5号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记
0分.如图是根据他们各自的累积得分绘制的条形统计图.之后来了第6号学生也按同样记分规定投了5次,其命中率为40%.
(1)求第6号学生的积分,并将图增补为这6名学生积分的条形统计图;
第3题图
解:(1)第6号学生的积分为5×40%×1=2(分).
增补的条形统计图如解图:
第3题解图
(2)在这6名学生中,随机选一名学生,求选上命中率高于50%的学生的概率;
(2)∵命中率高于50%,且积分为整数,
∴累积得分应至少3分,
∴这6名学生中,有4名学生的命中率高于50%,
∴P(选上命中率高于50%的学生)=
;
(3)∵前6名学生的积分中3出现的次数最多,
∴前6名学生积分的众数是3分,
∴7名学生积分的众数是3分,
∴第7号学生命中了3次或没有命中,
∴第7号学生的积分是3分或0分.
(3)最后,又来了第7号学生,也按同样记分规定投了5次.这时7名学生积分的众数仍是前6名学生积分的众数,求这个众数,以及第7号学生的积分.
4.
(2018河北21题9分)老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图①)和不完整的扇形图(图②),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数;
第4题图
解:(1)∵由条形统计图可知,读书6册的有6人,由扇形统计图可知,读书6册的人数占总调查人数的25%,
∴调查人数为6÷25%=24(人),(1分)
∴读书5册的人数为24-5-6-4=9(人),
即被遮盖的数为9;(2分)
∵调查人数为24人,
∴读书册数的中位数为由小到大(或由大到小)排序后第12人和第13人读书册数的平均数,
∵第12人和第13人的读书册数均为5册,
∴册数的中位数是5册;(3分)
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
第4题图
(2)∵读书超过5册的共有6+4=10(人),
∴P(选中读书超过5册的学生)=
;(6分)
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了________人.
(3)3.
(9分)
第4题图
5.
(2019河北22题9分)某球室有三种品牌的4个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知P(一次拿到8元球)=
.
(1)求这4个球价格的众数;
解:(1)∵P(一次拿到8元球)=
,
∴8元球为2个,
∴四个乒乓球的价格为7、8、8、9,
∴这四个球价格的众数为8;(3分)
(2)若甲组已拿走一个7元球训练,乙组准备从剩余3个球中随机拿一个训练.
①所剩的3个球价格的中位数与原来4个球价格的中位数是否相同?并简要说明理由;
(2)①相同;(4分)
理由:原四个球的中位数为8,拿走一个7元球后,剩余球的价格为8、8、9,
中位数为8,与原来4个球价格的中位数相同;(6分)
②列表如下:
又拿
先拿
8
8
9
8
(8,8)
(8,8)
(8,9)
8
(8,8)
(8,8)
(8,9)
9
(9,8)
(9,8)
(9,9)
由列表可知,共有9种等可能的结果,其中乙组两次都拿到8元球的结果共4种,
∴P(乙组两次都拿到8元球)=
.(9分)
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如图)求乙组两次都拿到8元球的概率.
又拿
先拿
类型三 概率与数轴结合(2020年考查)
6.
(2020河北25题10分)如图,甲、乙两人(看成点)分别在数轴-3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.
①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;
②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;
③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.
第6题图
(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;
解:(1)依题意,得移动一次共有4种等可能的情况,只有甲对乙错时,甲才能停留在正半轴上,
∴P(甲的位置停留在正半轴上)=
;(3分)
第6题图
(2)从图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值;
(2)依题意,得m=5+(-4)n+2(10-n)=25-6n.
当表示乙的点离原点O最近时,|m|取最小值,此时n=4,
∴表示乙的点离原点最近时n的值为4;(6分)
第6题图
(3)k的值为3或5.(10分)
第6题图
(3)从图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.
事件
的分类
确定事件
随机事件
概率
的计算
直接公式法
列表法
画树状图法
频率估计概率
几何概型的概率公式
概率
【课标要求】
◎能通过列表、画树状图等方法列出简单随机事件所有可能的结果,以及指定事件发生的所有可能的结果,了解事件的概率;
◎知道通过大量的重复试验,可以用频率来估计概率.
【对接教材】冀教:九下第三十一章P60-P80;
人教:九上第二十五章P126-P153;
北师:七下第六章P135-P159,九上第三章P59-P74.
考点
1
事件的分类
确定事件
必然事件:在一定条件下,必然会发生的事件,概率P=________
不可能事件:在一定条件下,不可能发生的事件,概率P=________
随机事件
在一定条件下,可能发生也可能不发生的事件,概率在0~1之间
1
0
考点
2
概率的计算
直接公式法
如果一个试验有n种可能的结果,事件A包含其中的m种结果,那么事件
A发生的概率为P(A)=________
列表法
如果一次试验涉及两个因素,并且只有有限个等可能的结果,结果数目较多时,通常采用列表法求事件发生的概率
画树状图法
当一次试验涉及三个或更多的因素时,通常采用画树状图法来求事件发生的概率
频率估计概率
一般地,做n次重复试验,如果事件A发生了m次,比值稳定于某个常数p.那么事件A发生的概率:P(A)=p
几何概型的概率公式
一、概率的计算
例 在一个不透明口袋中有四个小球,分别标有数字-3,0,1,2,每个小球除数字不同外其余均相同,每次试验先摇匀.
(1)从中摸出一个球,数字为3是________事件,从中摸出3个球,至少有1个正数是________事件,从中摸出2个球,有一个数字是0是______事件;
(2)从中随机取一个小球,则取出的小球上的数字为负数的概率为________;
(3)若再向口袋中放入n个标有负数的小球摇匀,再从不透明口袋中取一个小球,摸到数字为正整数的概率为
,则加入的小球个数n为________;
随机
不可能
必然
4
(4)先从口袋中随机取一个小球,记下小球上的数字,再从剩下的小球中随机取一个小球,再记下小球上的数字.求两次取出的小球上的数字之和是奇数的概率;
(4)根据题意列表如下:
第一
次
数字之和
第
二次
-3
0
1
2
-3
-3
-2
-1
0
-3
1
2
1
-2
1
3
2
-1
2
3
由列表可知,共有12种等可能的情况,两个数字之和是奇数的情况有8种,
∴P(两次取出的小球上的数字之和是奇数)=
;
(5)先从口袋中随机取一个小球,记下小球上的数字,放回搅拌均匀后,再从中随机取一个小球,再记下小球上的数字,求两次取出的小球上的数字之积为2的概率;
(5)根据题意列表如下:
由上表可知,共有16种等可能的情况,其中两次取出的小球上数字之积为2的情况有2种,
∴P(两次取出的小球上的数字之积为2)=
.
第一
次
数字之积
第
二次
-3
0
1
2
-3
9
0
-3
-6
0
0
0
0
0
1
-3
0
1
2
2
-6
0
2
4
(6)嘉嘉和淇淇同时从该口袋中随机各取出一个小球,若两个小球上数字均为正整数,则嘉嘉获胜,反之则淇淇获胜,这个游戏公平吗,请说明理由.若不公平,请你设计出一个公平的游戏.
(6)不公平.理由:根据题意列表如下:
嘉嘉
淇淇
-3
0
1
2
-3
(-3,0)
(-3,1)
(-3,2)
0
(0,-3)
(0,1)
(0,2)
1
(1,-3)
(1,0)
(1,2)
2
(2,-3)
(2,0)
(2,1)
由列表可知,共有12种等可能的情况,
其中两个小球上数字均为正整数的情况有2种,
∴P(嘉嘉获胜)=
,
P(淇淇获胜)=
.
∵P(嘉嘉获胜)≠P(淇淇获胜),
∴不公平.
公平的游戏可以设计为:从该口袋中随机取两个小球,这两个小球上数字之和大于0,则嘉嘉获胜,小于0,则淇淇获胜.(答案不唯一)
练习1 (2020泰州)如图,电路图上有4个开关A、B、C、D和1个小灯泡,同时闭合开关A、B或同时闭合开关C、D都可以使小灯泡发光.下列操作中,“小灯泡发光”这个事件是随机事件的是( )
A.
只闭合1个开关 B.
只闭合2个开关
C.
只闭合3个开关
D.
闭合4个开关
练习1题图
B
练习2 如图,一个圆形转盘被等分为八个扇形区域,上面分别标有数字1、2、3、5,转盘指针的位置固定,转动转盘后任其自由停止.转动转盘一次,当转盘停止时,记指针指向标有“3”所在区域的概率为P(3),指针指向标有“5”所在区域的概率为P(5),则P(3)______P(5).(填“>”“
=”或“<”
)
练习2题图
>
二、统计与概率结合
练习3 (2020河北大模考)在抗击新型冠状病毒肺炎战役中,某市党员积极响应国家号召参加志愿者活动,为人民服务,现随机抽查部分党员一个月来参加志愿者活动的次数,并绘制成如下尚不完整的条形统计图(图①)和扇形统计图(图②).
图①
图②
练习3题图
(1)“4次”所在扇形的圆心角度数是________,请补全条形统计图;
72°
(1)补全条形统计图如解图所示;
练习3题解图
(2)∵随机抽查的党员人数为10÷20%=50(人),其中参加志愿者活动次数不少于3次的有14+10+8=32(人),
∴P(该党员一个月来参加志愿者活动次数不少于3次)=
;
(2)若从抽查的党员中随机选择一位接受媒体的采访,求该党员一个月来参加志愿者活动次数不少于3次的概率;
(3)设随机抽查的党员一个月来参加志愿者活动次数的中位数为a,若去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为b,当b>a时,求最少去掉了几名党员参加志愿者活动的次数.
(3)将参加次数按由小到大进行排列,可得中位数为第25、26个数的平均数,由题意得a=
=3,
∵去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为b,且b>a,
∴b=4或5.当b=4时,最少需去掉10名党员参加志愿者活动的次数,即去掉5个参加志愿者活动次数为2次的和5个参加志愿者活动次数为3次的;
当b=5时,最少需去掉17名党员参加志愿者活动的次数,
即去掉7个参加活动为2次的,7个参加活动为3次的,3个参加活动为4次的,
∵10<17,
∴b=4.
这时最少去掉了10名党员这一个月来参加志愿者活动的次数,即去掉5个参加志愿者活动次数为2次的和5个参加志愿者活动次数为3次的.
类型一 以数字为背景的概率计算(10年3考
)
1.
(2015河北13题2分)将一质地均匀的正方体骰子抛掷一次,观察向上一面的点数,与点数3相差2的概率是( )
A.
B.
C.
D.
B
2.
(2016河北23题9分)如图①,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.
如图②,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;…
设游戏者从圈A起跳.
(1)嘉嘉随机掷一次骰子,求落回到圈A的概率P1;
第2题图
解:(1)∵掷一次质地均匀的正四面体骰子有4种等可能结果,只有掷得4时,才会落回到圈A,
∴P1(落回到圈A)=
;
(2)淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2,并指出她与嘉嘉落回到圈A的可能性一样吗?
第2题图
(2)列表如下:
第一次
第二次
1
2
3
4
1
(1,1)
(2,1)
(3,1)
(4,1)
2
(1,2)
(2,2)
(3,2)
(4,2)
3
(1,3)
(2,3)
(3,3)
(4,3)
4
(1,4)
(2,4)
(3,4)
(4,4)
∴P2(最后落回到圈A)=
,
∵P1=P2=
,
∴淇淇与嘉嘉落回到圈A的可能性一样.
由列表可知,共有16种等可能的结果,当两次掷得的数字和为4的倍数,即(1,3),(2,2),(3,1),(4,4)时,才可落回到圈A,共有4种,
类型二 与统计结合的概率计算(10年3考
)
3.
(2017河北21题9分)编号为1~5号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记
0分.如图是根据他们各自的累积得分绘制的条形统计图.之后来了第6号学生也按同样记分规定投了5次,其命中率为40%.
(1)求第6号学生的积分,并将图增补为这6名学生积分的条形统计图;
第3题图
解:(1)第6号学生的积分为5×40%×1=2(分).
增补的条形统计图如解图:
第3题解图
(2)在这6名学生中,随机选一名学生,求选上命中率高于50%的学生的概率;
(2)∵命中率高于50%,且积分为整数,
∴累积得分应至少3分,
∴这6名学生中,有4名学生的命中率高于50%,
∴P(选上命中率高于50%的学生)=
;
(3)∵前6名学生的积分中3出现的次数最多,
∴前6名学生积分的众数是3分,
∴7名学生积分的众数是3分,
∴第7号学生命中了3次或没有命中,
∴第7号学生的积分是3分或0分.
(3)最后,又来了第7号学生,也按同样记分规定投了5次.这时7名学生积分的众数仍是前6名学生积分的众数,求这个众数,以及第7号学生的积分.
4.
(2018河北21题9分)老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图①)和不完整的扇形图(图②),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数;
第4题图
解:(1)∵由条形统计图可知,读书6册的有6人,由扇形统计图可知,读书6册的人数占总调查人数的25%,
∴调查人数为6÷25%=24(人),(1分)
∴读书5册的人数为24-5-6-4=9(人),
即被遮盖的数为9;(2分)
∵调查人数为24人,
∴读书册数的中位数为由小到大(或由大到小)排序后第12人和第13人读书册数的平均数,
∵第12人和第13人的读书册数均为5册,
∴册数的中位数是5册;(3分)
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
第4题图
(2)∵读书超过5册的共有6+4=10(人),
∴P(选中读书超过5册的学生)=
;(6分)
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了________人.
(3)3.
(9分)
第4题图
5.
(2019河北22题9分)某球室有三种品牌的4个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知P(一次拿到8元球)=
.
(1)求这4个球价格的众数;
解:(1)∵P(一次拿到8元球)=
,
∴8元球为2个,
∴四个乒乓球的价格为7、8、8、9,
∴这四个球价格的众数为8;(3分)
(2)若甲组已拿走一个7元球训练,乙组准备从剩余3个球中随机拿一个训练.
①所剩的3个球价格的中位数与原来4个球价格的中位数是否相同?并简要说明理由;
(2)①相同;(4分)
理由:原四个球的中位数为8,拿走一个7元球后,剩余球的价格为8、8、9,
中位数为8,与原来4个球价格的中位数相同;(6分)
②列表如下:
又拿
先拿
8
8
9
8
(8,8)
(8,8)
(8,9)
8
(8,8)
(8,8)
(8,9)
9
(9,8)
(9,8)
(9,9)
由列表可知,共有9种等可能的结果,其中乙组两次都拿到8元球的结果共4种,
∴P(乙组两次都拿到8元球)=
.(9分)
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如图)求乙组两次都拿到8元球的概率.
又拿
先拿
类型三 概率与数轴结合(2020年考查)
6.
(2020河北25题10分)如图,甲、乙两人(看成点)分别在数轴-3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.
①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;
②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;
③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.
第6题图
(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;
解:(1)依题意,得移动一次共有4种等可能的情况,只有甲对乙错时,甲才能停留在正半轴上,
∴P(甲的位置停留在正半轴上)=
;(3分)
第6题图
(2)从图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值;
(2)依题意,得m=5+(-4)n+2(10-n)=25-6n.
当表示乙的点离原点O最近时,|m|取最小值,此时n=4,
∴表示乙的点离原点最近时n的值为4;(6分)
第6题图
(3)k的值为3或5.(10分)
第6题图
(3)从图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.
同课章节目录
