北师大版八年级数学下册第一章1.2.2直角三角形课件(共18张)
文档属性
| 名称 | 北师大版八年级数学下册第一章1.2.2直角三角形课件(共18张) |  | |
| 格式 | pptx | ||
| 文件大小 | 796.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 16:51:59 | ||
图片预览






文档简介
北师大版八年级数学下册第一章
1.2.2直角三角形
学习目标
1.能够证明直角三角形全等的“HL”判定定理; 2.能根据“HL”定理解决实际问题。
温故知新
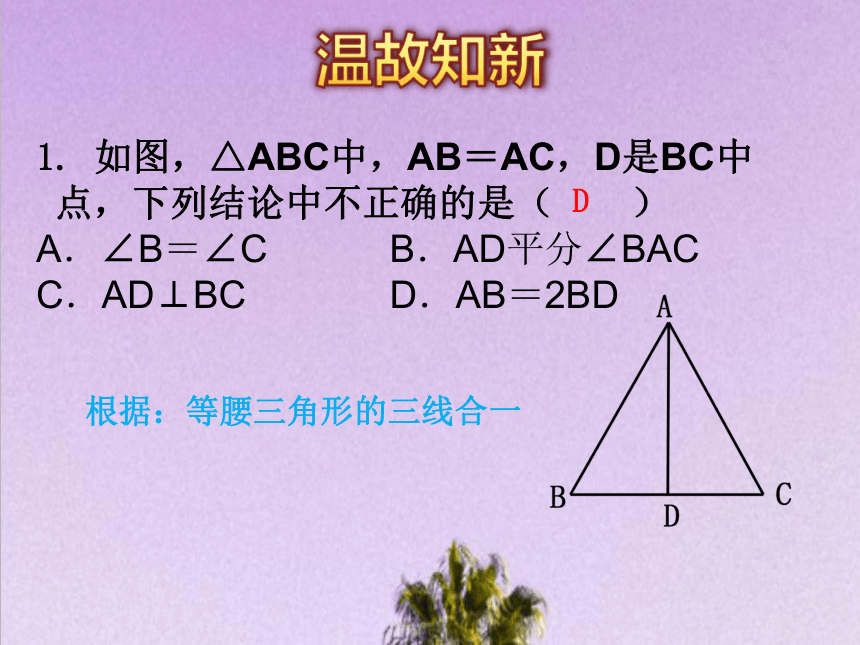
1. 如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是( )
A.∠B=∠C B.AD平分∠BAC
C.AD⊥BC D.AB=2BD
D
根据:等腰三角形的三线合一
2.在Rt△ABC中,a.b.c为三角形的三边长,已知a=3,b=4,则c2 = .
温故知新
25 或7
C
此题没有指明哪个角是直角,需要进行“分类讨论”
3.三角形的三边长为 ,则这个三角形是( ) A.等边三角形 B.钝角三角形
C.直角三角形 D.锐角三角形
4.三角形全等的判定方法有 。
温故知新
SSS,SAS,ASA,AAS
自主探究
问题1:两边及其中一边的对角对应相等的两个三角形全等吗?如果其中一边所对的角是直角呢?请证明你认为正确的结论.
两边及其中一边的对角对应相等的两个三角
形不一定全等
如果其中一边所对的角是直角,两个三角
形一定全等
做一做:已知一条直角边和斜边,求作一个直角三角形。
已知: 求作:
线段a,c,∠a=90°
△ABC,使∠C=∠a=90°,CB=a,AB=c
作法:1.作∠MCN=90°
2.在CM上截取CB=a,
3.以点B为圆心,以c为半径画弧,交CN于点A,
4.连接AB
则△ABC为所求作的三角形
结论: .
斜边和直角边对应相等的两个直角三角形全等(HL)
例1.如图,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
典型例题
解:∠B和∠F互余
理由:∵AC⊥AB,ED⊥DF
∴∠CAB=∠EDF=90°
在Rt△ABC和Rt△DEF中
∵BC=EF,AC=DF
∴Rt△ABC≌Rt△DEF(HL)
∴∠BCA=∠F
∵∠B+∠BCA=90°
∴∠B+∠F=90°
例2. D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别为E.F,且DE=DF,
求证:BF=CE
典型例题
证明:∵D是BC边上的中点,
∴DB=DC
∵DE⊥AC,DF⊥AB
∴∠DFB=∠DEC=90°
在Rt△BFD和Rt△CED中
∵BD=CD,DF=DE
∴Rt△BFD≌Rt△CED(HL)
∴BF=CE
典型例题
例3.在如图所示的三角形纸片ABC中,∠C=90°,∠B=30°,按如下步骤可以把这个直角三角形纸片分成三个全等的小直角三角形(图中虚线表示折痕): ①先将点B对折到点A,②将对折后的纸片再沿AD对折.(1)由步骤①可以得到哪些等量关系?(2)请证明△ACD≌△AED;(3)按照这种方法能否将任意一个直角三角形分成三个全等的小三角形.
解:(1)AD=BD,AE=BE
(2)在Rt△ABC中,∠C=90°,∠B=30°
∴∠CAB=60°
由折叠可得∠DAB=∠B=30°,∠DEA=∠DEB=90°
∴∠DAB=∠CAD=30°,∠DEA=∠DCA=90°
又∵AD=AD
∴△ACD≌△AED(AAS)
(3)不能
1.下列各选项中的两个直角三角形不一定全等的是( ) A.两条直角边对应相等的两个直角三角形. B.两条锐角边对应相等的两个直角三角形. C.斜边和一条直角边对应相等的两个直角三角形. D.有一个锐角及这个锐角的对边对应相等的两个直角三角形全等.
随堂练习
B
2.下列长度的三条线段能构成直角三角形的是( ) ①8,15,17 ②4,5,6 ③7.5,4.8,5 ④ 24,25,7 ⑤ 5,8,10 A.①②④ B.②④⑤
C.①③⑤ D.①③④
随堂练习
D
3.下列命题中,假命题是( ) A.三个角的度数之比为1:3:4的三角形是直角三角形. B.三个角的度数之比为1:3:2的三角形是直角三角形. C.三边长之比为 的三角形是直角三角形. D.三边长之比为 的三角形是直角三角形.
随堂练习
D
4.如图,两根长度均为12m的绳子,一端系在旗杆上,另一端分别固定在地面的两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明理由
随堂练习
解:两个木桩离旗杆底部的距离相等.
理由如下:∵AB=AC,AD⊥BC,∴∠ADB=∠ADC=90°.
在Rt△ABD和Rt△ACD中,
AB=AC,AD=AD,
∴Rt△ABD≌Rt△ACD.
∴BD=CD.
1.下列说法正确的有( ) (1)一个锐角及斜边对应相等的两个直角三角形全等. (2)一个锐角及一条直角边对应相等的两个直角三角形全等. (3)两个锐角对应等的两个直角三角形全等. (4)有两条边相等的两个直角三角形全等. (5)有斜边和一条直角边对应相等的两个直角三角形全等. A.2个 B.3个 C.4个 D.5个
当堂检测
B
2.四边形ABCD中,若AB=3,BC=4,CD=12,AD=13,且AB⊥BC,求四边形ABCD的面积________.
当堂检测
36
3.如图已知∠ACB=∠BDA=90°,要使△ACB≌△BDA,还需要什么条件?把它们分别写出来.
当堂检测
解:∠CAB=∠DBA
或∠ABC=∠BAC
或AC=DB
或BC=AD
1.2.2直角三角形
学习目标
1.能够证明直角三角形全等的“HL”判定定理; 2.能根据“HL”定理解决实际问题。
温故知新
1. 如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是( )
A.∠B=∠C B.AD平分∠BAC
C.AD⊥BC D.AB=2BD
D
根据:等腰三角形的三线合一
2.在Rt△ABC中,a.b.c为三角形的三边长,已知a=3,b=4,则c2 = .
温故知新
25 或7
C
此题没有指明哪个角是直角,需要进行“分类讨论”
3.三角形的三边长为 ,则这个三角形是( ) A.等边三角形 B.钝角三角形
C.直角三角形 D.锐角三角形
4.三角形全等的判定方法有 。
温故知新
SSS,SAS,ASA,AAS
自主探究
问题1:两边及其中一边的对角对应相等的两个三角形全等吗?如果其中一边所对的角是直角呢?请证明你认为正确的结论.
两边及其中一边的对角对应相等的两个三角
形不一定全等
如果其中一边所对的角是直角,两个三角
形一定全等
做一做:已知一条直角边和斜边,求作一个直角三角形。
已知: 求作:
线段a,c,∠a=90°
△ABC,使∠C=∠a=90°,CB=a,AB=c
作法:1.作∠MCN=90°
2.在CM上截取CB=a,
3.以点B为圆心,以c为半径画弧,交CN于点A,
4.连接AB
则△ABC为所求作的三角形
结论: .
斜边和直角边对应相等的两个直角三角形全等(HL)
例1.如图,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
典型例题
解:∠B和∠F互余
理由:∵AC⊥AB,ED⊥DF
∴∠CAB=∠EDF=90°
在Rt△ABC和Rt△DEF中
∵BC=EF,AC=DF
∴Rt△ABC≌Rt△DEF(HL)
∴∠BCA=∠F
∵∠B+∠BCA=90°
∴∠B+∠F=90°
例2. D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别为E.F,且DE=DF,
求证:BF=CE
典型例题
证明:∵D是BC边上的中点,
∴DB=DC
∵DE⊥AC,DF⊥AB
∴∠DFB=∠DEC=90°
在Rt△BFD和Rt△CED中
∵BD=CD,DF=DE
∴Rt△BFD≌Rt△CED(HL)
∴BF=CE
典型例题
例3.在如图所示的三角形纸片ABC中,∠C=90°,∠B=30°,按如下步骤可以把这个直角三角形纸片分成三个全等的小直角三角形(图中虚线表示折痕): ①先将点B对折到点A,②将对折后的纸片再沿AD对折.(1)由步骤①可以得到哪些等量关系?(2)请证明△ACD≌△AED;(3)按照这种方法能否将任意一个直角三角形分成三个全等的小三角形.
解:(1)AD=BD,AE=BE
(2)在Rt△ABC中,∠C=90°,∠B=30°
∴∠CAB=60°
由折叠可得∠DAB=∠B=30°,∠DEA=∠DEB=90°
∴∠DAB=∠CAD=30°,∠DEA=∠DCA=90°
又∵AD=AD
∴△ACD≌△AED(AAS)
(3)不能
1.下列各选项中的两个直角三角形不一定全等的是( ) A.两条直角边对应相等的两个直角三角形. B.两条锐角边对应相等的两个直角三角形. C.斜边和一条直角边对应相等的两个直角三角形. D.有一个锐角及这个锐角的对边对应相等的两个直角三角形全等.
随堂练习
B
2.下列长度的三条线段能构成直角三角形的是( ) ①8,15,17 ②4,5,6 ③7.5,4.8,5 ④ 24,25,7 ⑤ 5,8,10 A.①②④ B.②④⑤
C.①③⑤ D.①③④
随堂练习
D
3.下列命题中,假命题是( ) A.三个角的度数之比为1:3:4的三角形是直角三角形. B.三个角的度数之比为1:3:2的三角形是直角三角形. C.三边长之比为 的三角形是直角三角形. D.三边长之比为 的三角形是直角三角形.
随堂练习
D
4.如图,两根长度均为12m的绳子,一端系在旗杆上,另一端分别固定在地面的两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明理由
随堂练习
解:两个木桩离旗杆底部的距离相等.
理由如下:∵AB=AC,AD⊥BC,∴∠ADB=∠ADC=90°.
在Rt△ABD和Rt△ACD中,
AB=AC,AD=AD,
∴Rt△ABD≌Rt△ACD.
∴BD=CD.
1.下列说法正确的有( ) (1)一个锐角及斜边对应相等的两个直角三角形全等. (2)一个锐角及一条直角边对应相等的两个直角三角形全等. (3)两个锐角对应等的两个直角三角形全等. (4)有两条边相等的两个直角三角形全等. (5)有斜边和一条直角边对应相等的两个直角三角形全等. A.2个 B.3个 C.4个 D.5个
当堂检测
B
2.四边形ABCD中,若AB=3,BC=4,CD=12,AD=13,且AB⊥BC,求四边形ABCD的面积________.
当堂检测
36
3.如图已知∠ACB=∠BDA=90°,要使△ACB≌△BDA,还需要什么条件?把它们分别写出来.
当堂检测
解:∠CAB=∠DBA
或∠ABC=∠BAC
或AC=DB
或BC=AD
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
