北师大版九年级数学下册 第3章圆第4课时垂径定理的应用及垂径定理的推论 课件(17张)
文档属性
| 名称 | 北师大版九年级数学下册 第3章圆第4课时垂径定理的应用及垂径定理的推论 课件(17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 917.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 19:13:36 | ||
图片预览


文档简介
第4课 垂径定理的应用及垂径定理的推论
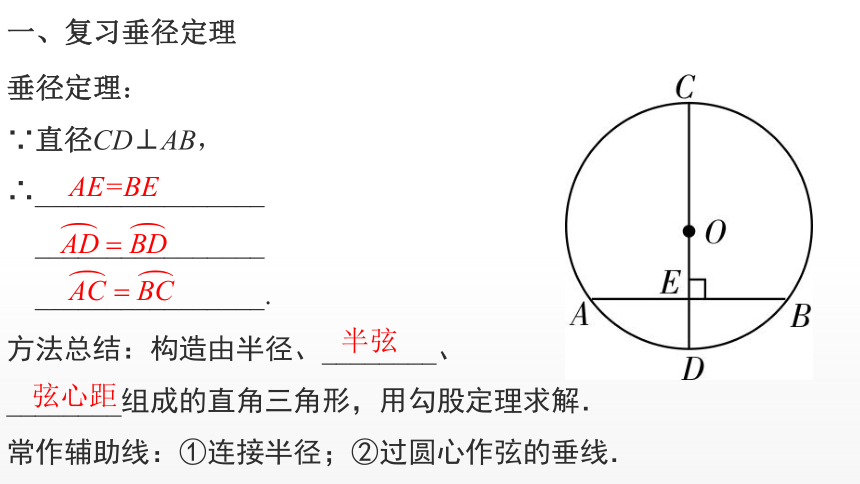
一、复习垂径定理
垂径定理:
∵直径CD⊥AB,
∴________________
________________
________________.
方法总结:构造由半径、________、
________组成的直角三角形,用勾股定理求解.
常作辅助线:①连接半径;②过圆心作弦的垂线.
AE=BE
半弦
弦心距
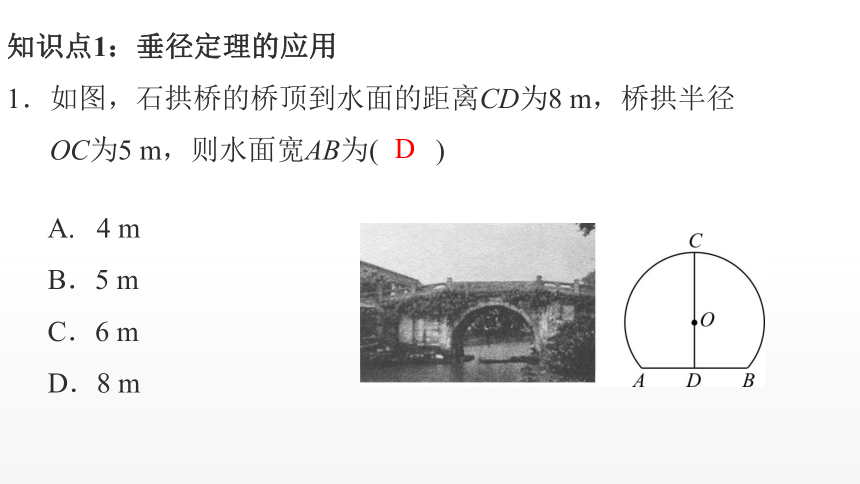
知识点1:垂径定理的应用
1.如图,石拱桥的桥顶到水面的距离CD为8 m,桥拱半径
OC为5 m,则水面宽AB为( )
A. 4 m
B.5 m
C.6 m
D.8 m
D
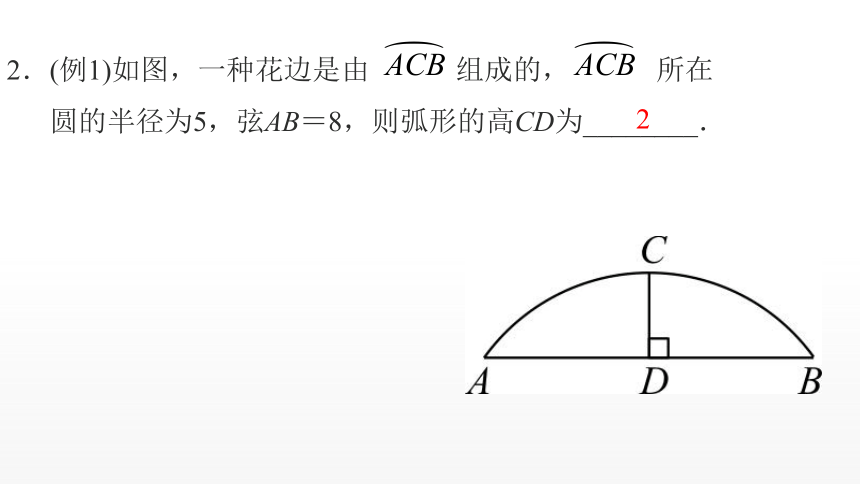
2.(例1)如图,一种花边是由 组成的, 所在
圆的半径为5,弦AB=8,则弧形的高CD为________.
2
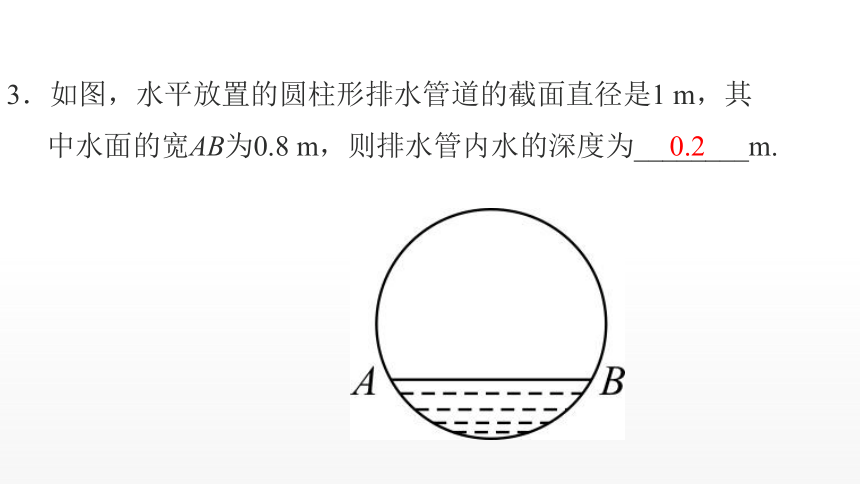
3.如图,水平放置的圆柱形排水管道的截面直径是1 m,其
中水面的宽AB为0.8 m,则排水管内水的深度为________m.
0.2
4.(引例)如图,CD为⊙O的直径,E为弦AB(不是直径)的
中点,请问CD与AB垂直吗?
解:垂直.理由如下:连接OA,OB.
∵E为AB中点,
∴AE=BE.
在△AOE和△BOE中,
∴△AOE≌△BOE.
∴∠AEO=∠BEO=90°.
∴CD⊥AB.
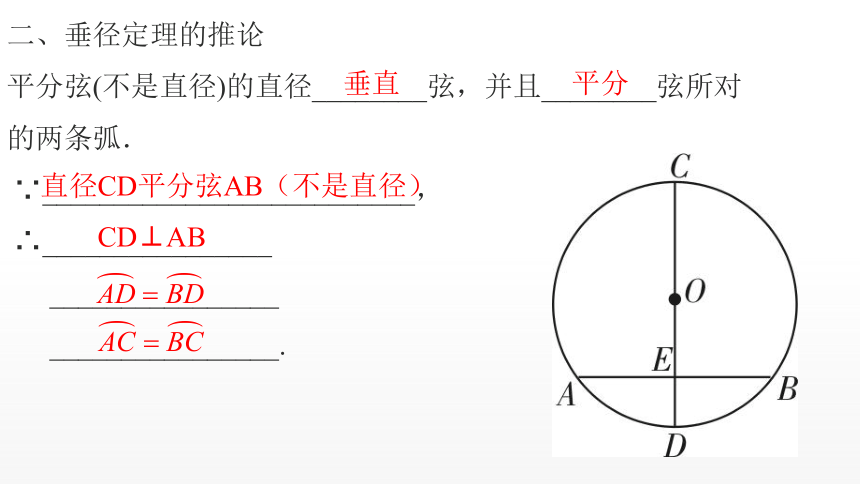
二、垂径定理的推论
平分弦(不是直径)的直径________弦,并且________弦所对的两条弧.
∵__________________________,
∴________________
________________
________________.
垂直
平分
直径CD平分弦AB(不是直径)
CD⊥AB
5.(例2)如图,C为弦AB的中点,CD=1,AB=10,求⊙O半径.
解:∵C为弦AB的中点,∴半径OD⊥AB
∴AC= AB= ×10=5
连接 OA,设OA=OD=x
在Rt△OAC中,CO=x-1
∵OC2+AC2=OA2
∴(x-1)2+52=x2
∴x=13
∴⊙O半径为13
6.如图,D为 的中点,⊙O半径为10,CD=4,求AB的长.
解:连接AO.
∵D为 的中点,∴OD⊥AB.
∴AC=BC= AB.
∵OA=OD=10,CD=4,
∴OC=10-4=6,
∴AC= ,
∴AB=2AC=16.
7.(例3)如图,AB为⊙O的直径,E为OB与CD的中点,CD=4 ,
求⊙O的周长.
解:连接OC,设 OC=OB=x
∵E为OB中点,∴OE= x
∵E为CD中点
∴OE⊥CD,CE= CD=2
在Rt△OCE中,OE2+EC2=OC2
即 +(2 )2=x2
解得x=4
∴⊙O的周长为2π·4=8π
8.如图,∠A=45°,C为⊙O的弦AB的中点,AB=2,求
⊙O的面积.
解:∵C为AB中点,
∴OC⊥AB,AC= AB=1,
∵∠A=45°,
∴AC=OC=1,
∴AO= ,
∴S⊙O=π·( )2=2π.
三、过关检测
第1关
9.如图,工程上常用钢珠来测量零件上小圆孔的宽口,假设
钢珠的直径是10 mm,测得钢珠顶端离零件表面的距离为
8 mm,则这个小圆孔的宽口AB的长度是________.
8 mm
10.如图,D为 的中点,CD=2,AB=12,求⊙O
的半径.
解:设⊙O的半径为x,连接OA,
则OA=OD=x,OC=x-2.
∵D为 的中点,
∴OD⊥AB,AC= AB=6
∴OA2=AC2+OC2,
即x2=62+(x-2)2,解得x=10
∴⊙O的半径为10.
第2关
11.如图,水管横截面⊙O半径为13 cm,水面宽AB=24 cm,
求水的最大深度.
解:过O作OC⊥AB,垂足为C,
延长CO交⊙O于D,连接OB.
在Rt△OBC中,OB=13 cm
BC= AB=12 cm
∴OC= (cm)
∴最大深度CD=OC+OD=5+13=18(cm)
12.如图,AC垂直平分⊙O的半径OB,垂足为P,四边形
OABC是什么特殊的四边形?证明你的结论.
解:菱形
证明如下:∵AC垂直平分OB
∴AC⊥OB,PO=PB
∴PA=PC
∴四边形OABC为平行四边形
∵AC⊥OB
∴ OABC为菱形
13.如图,在⊙O中,AB∥A′B′.求证: .
证明:如图,过O作OE⊥AB交⊙O于E
∵AB∥A′B′
∴OE⊥A′B′
∴
∵OE⊥AB
∴
∴
∴
14.如图,⊙O直径AB=4,E为OB中点,∠OED=30°,求
弦CD的长.
解:如图,过O作OF⊥CD, 连接OD,
∵E为OB中点,OB=2 ,∴OE=1
∵∠OED=30°
∴OF= OE=
在Rt△ODF中
DF=
∵OF⊥CD,∴CD=2DF=
一、复习垂径定理
垂径定理:
∵直径CD⊥AB,
∴________________
________________
________________.
方法总结:构造由半径、________、
________组成的直角三角形,用勾股定理求解.
常作辅助线:①连接半径;②过圆心作弦的垂线.
AE=BE
半弦
弦心距
知识点1:垂径定理的应用
1.如图,石拱桥的桥顶到水面的距离CD为8 m,桥拱半径
OC为5 m,则水面宽AB为( )
A. 4 m
B.5 m
C.6 m
D.8 m
D
2.(例1)如图,一种花边是由 组成的, 所在
圆的半径为5,弦AB=8,则弧形的高CD为________.
2
3.如图,水平放置的圆柱形排水管道的截面直径是1 m,其
中水面的宽AB为0.8 m,则排水管内水的深度为________m.
0.2
4.(引例)如图,CD为⊙O的直径,E为弦AB(不是直径)的
中点,请问CD与AB垂直吗?
解:垂直.理由如下:连接OA,OB.
∵E为AB中点,
∴AE=BE.
在△AOE和△BOE中,
∴△AOE≌△BOE.
∴∠AEO=∠BEO=90°.
∴CD⊥AB.
二、垂径定理的推论
平分弦(不是直径)的直径________弦,并且________弦所对的两条弧.
∵__________________________,
∴________________
________________
________________.
垂直
平分
直径CD平分弦AB(不是直径)
CD⊥AB
5.(例2)如图,C为弦AB的中点,CD=1,AB=10,求⊙O半径.
解:∵C为弦AB的中点,∴半径OD⊥AB
∴AC= AB= ×10=5
连接 OA,设OA=OD=x
在Rt△OAC中,CO=x-1
∵OC2+AC2=OA2
∴(x-1)2+52=x2
∴x=13
∴⊙O半径为13
6.如图,D为 的中点,⊙O半径为10,CD=4,求AB的长.
解:连接AO.
∵D为 的中点,∴OD⊥AB.
∴AC=BC= AB.
∵OA=OD=10,CD=4,
∴OC=10-4=6,
∴AC= ,
∴AB=2AC=16.
7.(例3)如图,AB为⊙O的直径,E为OB与CD的中点,CD=4 ,
求⊙O的周长.
解:连接OC,设 OC=OB=x
∵E为OB中点,∴OE= x
∵E为CD中点
∴OE⊥CD,CE= CD=2
在Rt△OCE中,OE2+EC2=OC2
即 +(2 )2=x2
解得x=4
∴⊙O的周长为2π·4=8π
8.如图,∠A=45°,C为⊙O的弦AB的中点,AB=2,求
⊙O的面积.
解:∵C为AB中点,
∴OC⊥AB,AC= AB=1,
∵∠A=45°,
∴AC=OC=1,
∴AO= ,
∴S⊙O=π·( )2=2π.
三、过关检测
第1关
9.如图,工程上常用钢珠来测量零件上小圆孔的宽口,假设
钢珠的直径是10 mm,测得钢珠顶端离零件表面的距离为
8 mm,则这个小圆孔的宽口AB的长度是________.
8 mm
10.如图,D为 的中点,CD=2,AB=12,求⊙O
的半径.
解:设⊙O的半径为x,连接OA,
则OA=OD=x,OC=x-2.
∵D为 的中点,
∴OD⊥AB,AC= AB=6
∴OA2=AC2+OC2,
即x2=62+(x-2)2,解得x=10
∴⊙O的半径为10.
第2关
11.如图,水管横截面⊙O半径为13 cm,水面宽AB=24 cm,
求水的最大深度.
解:过O作OC⊥AB,垂足为C,
延长CO交⊙O于D,连接OB.
在Rt△OBC中,OB=13 cm
BC= AB=12 cm
∴OC= (cm)
∴最大深度CD=OC+OD=5+13=18(cm)
12.如图,AC垂直平分⊙O的半径OB,垂足为P,四边形
OABC是什么特殊的四边形?证明你的结论.
解:菱形
证明如下:∵AC垂直平分OB
∴AC⊥OB,PO=PB
∴PA=PC
∴四边形OABC为平行四边形
∵AC⊥OB
∴ OABC为菱形
13.如图,在⊙O中,AB∥A′B′.求证: .
证明:如图,过O作OE⊥AB交⊙O于E
∵AB∥A′B′
∴OE⊥A′B′
∴
∵OE⊥AB
∴
∴
∴
14.如图,⊙O直径AB=4,E为OB中点,∠OED=30°,求
弦CD的长.
解:如图,过O作OF⊥CD, 连接OD,
∵E为OB中点,OB=2 ,∴OE=1
∵∠OED=30°
∴OF= OE=
在Rt△ODF中
DF=
∵OF⊥CD,∴CD=2DF=
