北师大版数学八年级下册 1.1.1等腰三角形课件(29张)
文档属性
| 名称 | 北师大版数学八年级下册 1.1.1等腰三角形课件(29张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览


文档简介
1.1等腰三角形
复习回顾
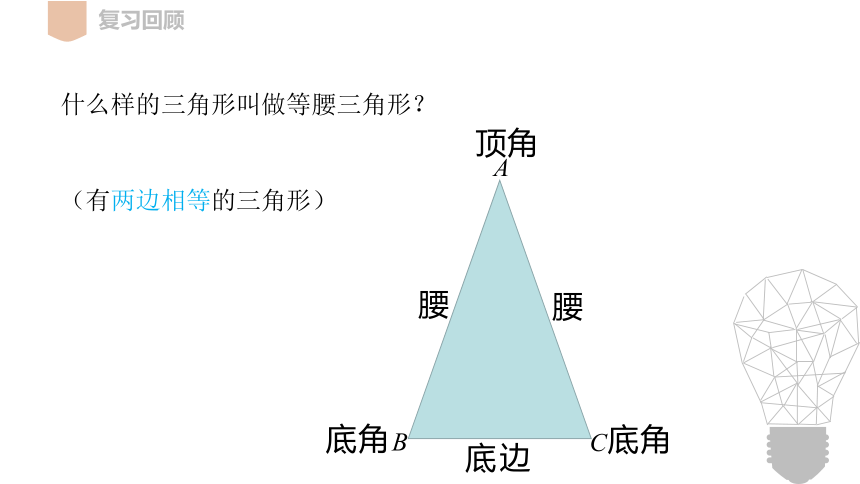
什么样的三角形叫做等腰三角形?
(有两边相等的三角形)
预习展示
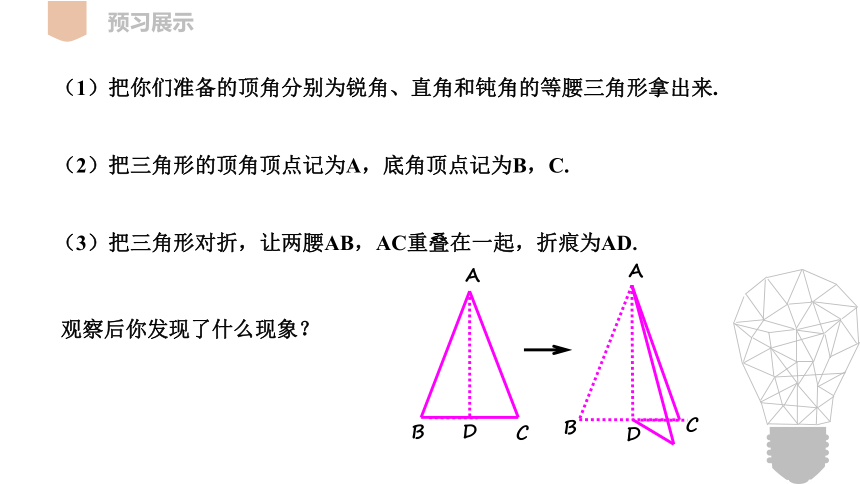
(1)把你们准备的顶角分别为锐角、直角和钝角的等腰三角形拿出来.
(2)把三角形的顶角顶点记为A,底角顶点记为B,C.
(3)把三角形对折,让两腰AB,AC重叠在一起,折痕为AD.
观察后你发现了什么现象?
B
A
C
D
A
B
C
D
结论
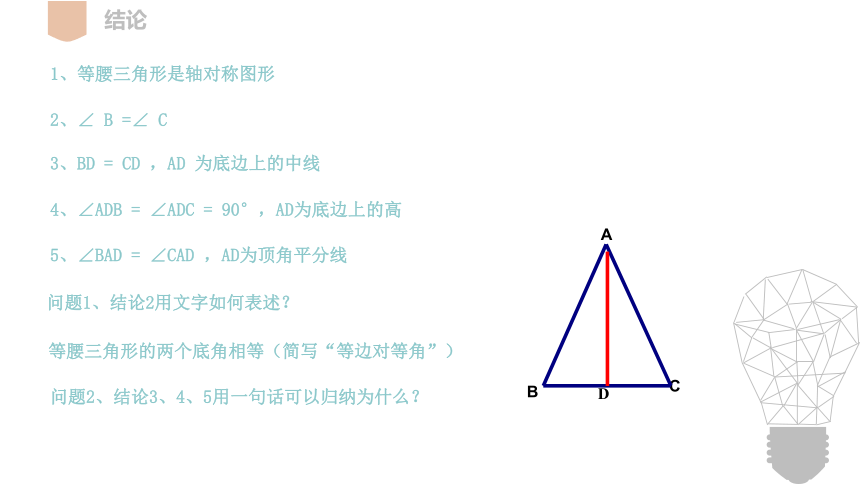
1、等腰三角形是轴对称图形
2、∠ B =∠ C
3、BD = CD ,AD 为底边上的中线
4、∠ADB = ∠ADC = 90°,AD为底边上的高
5、∠BAD = ∠CAD ,AD为顶角平分线
问题1、结论2用文字如何表述?
等腰三角形的两个底角相等(简写“等边对等角”)
问题2、结论3、4、5用一句话可以归纳为什么?
C
A
B
D
性质定理
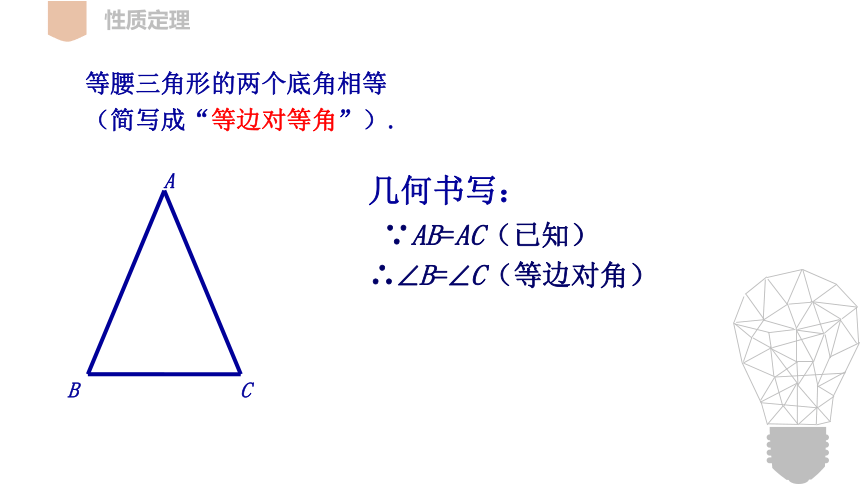
等腰三角形的两个底角相等
(简写成“等边对等角”).
C
A
B
几何书写:
∵AB=AC(已知)
∴?B=?C(等边对角)
推论
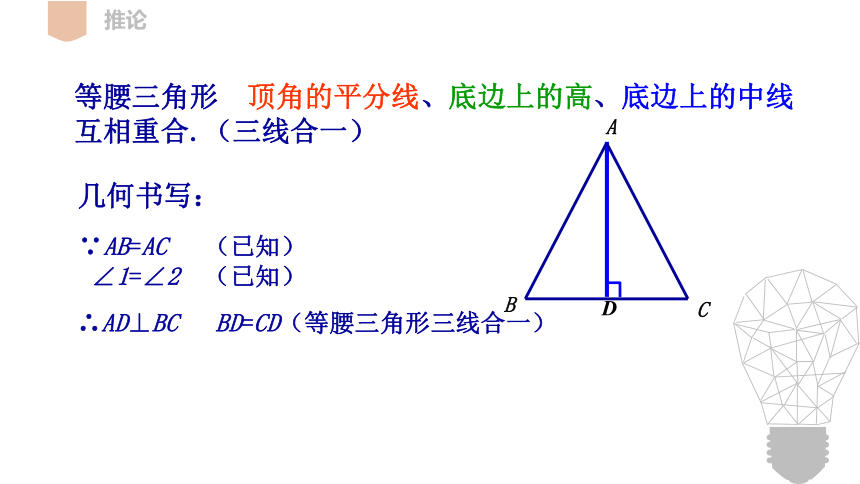
等腰三角形 顶角的平分线、底边上的高、底边上的中线 互相重合.(三线合一)
几何书写:
∵AB=AC (已知)
∠1=∠2 (已知)
∴AD⊥BC BD=CD(等腰三角形三线合一)
D
C
A
B
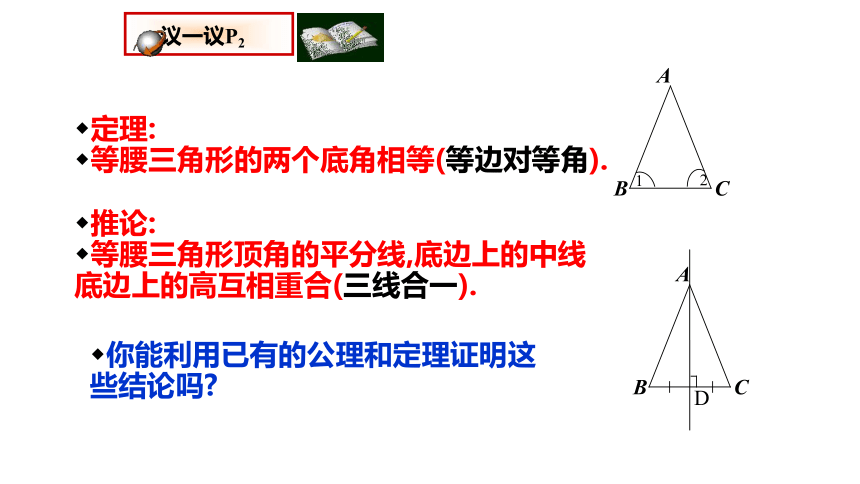
推论:
等腰三角形顶角的平分线,底边上的中线 底边上的高互相重合(三线合一).
你能利用已有的公理和定理证明这些结论吗?
议一议P2
定理:
等腰三角形的两个底角相等(等边对等角).
A
C
B
1
2
A
C
B
D
证明命题的一般步骤:
(1)理解题意:分清命题的条件(已知),结论(求证);
(2)根据题意,画出图形;
(3)结合图形,用符号语言写出“已知”和“求证”;
(4)分析题意,探索证明思路(由“因”导“果”,执“果”索“因”.);
(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程;
(6)检查表达过程是否正确,完善.
回顾与思考
?
与同伴交流你在探索思路的过程中的具体做法.
回顾与思考
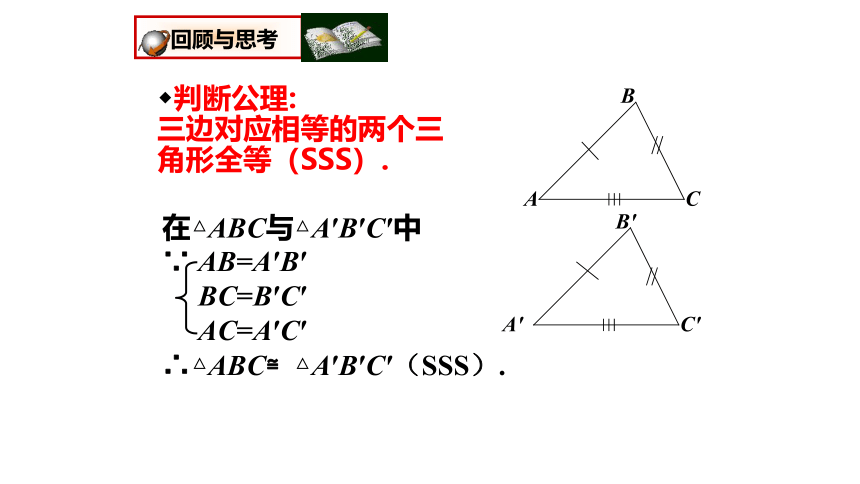
判断公理:
三边对应相等的两个三角形全等(SSS).
A
B
C
A′
B′
C′
在△ABC与△A′B′C′中
∵ AB=A′B′
BC=B′C′
AC=A′C′
∴△ABC≌△A′B′C′(SSS).
回顾与思考
判断公理:
两边及其夹角对应相等的两个三角形全等(SAS).
在△ABC与△A′B′C′中
∵ AB=A′B′
∠A=∠A′
BC=B′C′
∴△ABC≌△A′B′C′(SAS).
A
B
C
A′
B′
C′
●
●
回顾与思考
判断公理:
两角及其夹边对应相等的两个三角形全等(ASA).
在△ABC与△A′B′C′中
∵ ∠A=∠A′
AB=A′B′
∠B=∠B′
∴△ABC≌△A′B′C′(ASA).
A
B
C
A′
B′
C′
●
●
● ●
● ●
回顾与思考
性质公理:
全等三角形的对应边、对应角相等.
∵ △ABC≌△A′B′C′
∴ AB=A′B′,BC=B′C′,AC=A′C′
(全等三角形的对应边相等);
∠A=∠A′,∠B=∠B′,∠C=∠C′
(全等三角形的对应角相等).
●
●
● ●
● ●
A
B
C
A′
B′
C′
● ● ●
● ● ●
三角形全等
判定公理:三边对应相等的两个三角形全等(SSS)
公理:两边及其夹角对应相等的两个三角形全等(SAS)
公理:两角及其夹边对应相等的两个三角形全等(ASA)
性质公理:全等三角形的对应边、对应角相等.
你能用上面的公理证明下面的推论吗?
推论:两角及其中一角的对应边相等的两个三角形全等(AAS)
命题的证明
证明:
∵ ∠A=∠A′,∠C=∠C′(已知)∴∠B=∠B′(三角形内角和定理)
在△ABC与△A′B′C′中
∵ ∠A=∠A′ (已知),
AB=A′B′(已知),
∠B=∠B′ (已证),
∴ △ABC≌△A′B′C′(ASA).
A
B
C
A′
B′
C′
●
●
● ●
● ●
已知:如图,在△ABC和△A′B′C′中, ∠A=∠A′, ∠C=∠C′, AB=A′B′.
求证:△ABC≌△A′B′C′.
几何的三种语言
回顾与思考
推论:
两角及其一角的对边对应相等的两个三角形全等(AAS).
在△ABC与△A′B′C′中
∵∠A=∠A′
∠C=∠C′
AB=A′B′
∴△ABC≌△A′B′C′(AAS).
A
B
C
A′
B′
C′
●
●
● ●
● ●
证明后的结论,以后可以直接运用.
证明等腰三角形的性质
证明:等腰三角形的两个底角相等
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
证明:
作顶角的平分线AD. 在△BAD和△CAD中,
AB=AC ( 已知 ),
∠ BAD= ∠ CAD ( 辅助线作法 ),
AD=AD (公共边)
∴ △BAD ≌ △CAD (SAS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
A
B
C
D
作顶角的平分线
证明等腰三角形的性质
证明:等腰三角形的两个底角相等
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
证明:作底边中线AD.
在△BAD和△CAD中,
AB=AC ( 已知 ),
BD=CD ( 辅助线作法 ),
AD=AD (公共边) ,
∴ △BAD ≌ △CAD (SSS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
A
B
C
D
作底边中线
证明等腰三角形的性质
证明:等腰三角形的两个底角相等
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
证明:作底边高线AD.
在Rt△BAD和△RtCAD中,
AB=AC ( 已知 ),
AD=AD (公共边) ,
∴ Rt △BAD ≌ Rt △CAD (HL).
∴ ∠ B= ∠C (全等三角形的对应角相等).
A
B
C
D
作底边的高线
推论: 等腰三角形顶角的平分线、底边上的中线、底边上的高线互相重合(三线合一).
A
C
B
D
1
2
做一做P3
3
1、等腰三角形的顶角的平分线,既是底边上
的中线,又是底边上的高。
应用格式:∵AB=AC ∠1=∠2(已知)
∴BD=DC AD⊥BC(等腰三角形三线合一)
2、等腰三角形的底边上中线,既是底边上的高,又是
顶角平分线。
应用格式:∵AB=AC BD=DC (已知)
∴AD⊥BC ∠1=∠2 (等腰三角形三线合一)
3、等腰三角形的底边上的高,既是底
边上的中线,又是顶角平分线。
应用格式:∵AB=AC AD⊥BC (已知)
∴BD=DC ∠1=∠2 (等腰三角形三线合一)
A
C
B
D
1
2
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高,看看它们是否重合?
不重合!
三线合一
“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高
练习
1、已知:在△ABC中,AB=AC,∠A=80。求∠C和∠B的度数.
解:
结论:
在等腰三角形中,已知一个角,可以求另外两个角.
∵ AB=AC,
∴ ∠C=∠B( 等边对等角)
∵ ∠A+∠B +∠C=180。(三角形内角和等于180。)
∠A=80。
∴ ∠B=∠C=50。
练习
2、已知△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
A
B
C
D
解: ∵ AB=AC,(已知)
∴ ∠ABC=∠C (等边对等角)
∵ BD=BC=AD, (已知)
∴ ∠C=∠BDC (等边对等角)
∠A=∠ABD
设∠A=x°,则∠ABD= x°,
∠BDC=2 x°, ∠C=2 x°,
X°
X°
2X°
2X°
根据题意得:x+2x+2x=180
x=36
即∠A=36°∠ABC =∠ACB=72°
练习
3、已知AD⊥ BC,试找出等腰三角形ABC (AB=AC)中,存在相等关系的量.
C
B
D
A
1
2
∠B=∠C
∠1=∠2
∠BDA=∠CDA=90°
BD=CD
练习
4、填空:在△ABC中,AB=AC, D 在BC上,
(1)如果AD⊥BC,那么∠BAD = ∠______,
BD = ______.
(2)如果∠BAD= ∠CAD,那么AD⊥___, BD = ___.
(3)如果BD=CD,那么∠BAD =∠ _____, AD⊥___,
∠ADB =∠ _____=___°
D
CAD
CD
BC
CD
CAD
BC
ADC
90
练习
5、在三角形ABC中,AB=AC,且AD ⊥BC,已知BD=2cm,求DC=___cm, BC=___cm?
C
B
D
A
1
2
∵ AB=AC ,AD ⊥BC(已知)
∴BD=CD(等腰三角形的高与底边上的中线重合)
即(等腰三角形三线合一)
∵BD=2cm(已知)
∴CD=2cm
课堂小结
通过本节课的学习,你有哪些收获?
定理:等边对等角
推论:“三线合一”
常用来证明两角相等,求等腰三角形各角的度数.
研究等腰三角形的有关问题时“三线”是常用的辅助线.
等 腰 三 角 形
课后思考
建筑工人在盖房子时,用一块等腰三
角板放在梁上,从顶点系一重物,如果系
重物的绳子正好经过三角板底边中点,就
说房梁是水平
的,你知道其中
反映了什么数学
原理?
感谢您的聆听
复习回顾
什么样的三角形叫做等腰三角形?
(有两边相等的三角形)
预习展示
(1)把你们准备的顶角分别为锐角、直角和钝角的等腰三角形拿出来.
(2)把三角形的顶角顶点记为A,底角顶点记为B,C.
(3)把三角形对折,让两腰AB,AC重叠在一起,折痕为AD.
观察后你发现了什么现象?
B
A
C
D
A
B
C
D
结论
1、等腰三角形是轴对称图形
2、∠ B =∠ C
3、BD = CD ,AD 为底边上的中线
4、∠ADB = ∠ADC = 90°,AD为底边上的高
5、∠BAD = ∠CAD ,AD为顶角平分线
问题1、结论2用文字如何表述?
等腰三角形的两个底角相等(简写“等边对等角”)
问题2、结论3、4、5用一句话可以归纳为什么?
C
A
B
D
性质定理
等腰三角形的两个底角相等
(简写成“等边对等角”).
C
A
B
几何书写:
∵AB=AC(已知)
∴?B=?C(等边对角)
推论
等腰三角形 顶角的平分线、底边上的高、底边上的中线 互相重合.(三线合一)
几何书写:
∵AB=AC (已知)
∠1=∠2 (已知)
∴AD⊥BC BD=CD(等腰三角形三线合一)
D
C
A
B
推论:
等腰三角形顶角的平分线,底边上的中线 底边上的高互相重合(三线合一).
你能利用已有的公理和定理证明这些结论吗?
议一议P2
定理:
等腰三角形的两个底角相等(等边对等角).
A
C
B
1
2
A
C
B
D
证明命题的一般步骤:
(1)理解题意:分清命题的条件(已知),结论(求证);
(2)根据题意,画出图形;
(3)结合图形,用符号语言写出“已知”和“求证”;
(4)分析题意,探索证明思路(由“因”导“果”,执“果”索“因”.);
(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程;
(6)检查表达过程是否正确,完善.
回顾与思考
?
与同伴交流你在探索思路的过程中的具体做法.
回顾与思考
判断公理:
三边对应相等的两个三角形全等(SSS).
A
B
C
A′
B′
C′
在△ABC与△A′B′C′中
∵ AB=A′B′
BC=B′C′
AC=A′C′
∴△ABC≌△A′B′C′(SSS).
回顾与思考
判断公理:
两边及其夹角对应相等的两个三角形全等(SAS).
在△ABC与△A′B′C′中
∵ AB=A′B′
∠A=∠A′
BC=B′C′
∴△ABC≌△A′B′C′(SAS).
A
B
C
A′
B′
C′
●
●
回顾与思考
判断公理:
两角及其夹边对应相等的两个三角形全等(ASA).
在△ABC与△A′B′C′中
∵ ∠A=∠A′
AB=A′B′
∠B=∠B′
∴△ABC≌△A′B′C′(ASA).
A
B
C
A′
B′
C′
●
●
● ●
● ●
回顾与思考
性质公理:
全等三角形的对应边、对应角相等.
∵ △ABC≌△A′B′C′
∴ AB=A′B′,BC=B′C′,AC=A′C′
(全等三角形的对应边相等);
∠A=∠A′,∠B=∠B′,∠C=∠C′
(全等三角形的对应角相等).
●
●
● ●
● ●
A
B
C
A′
B′
C′
● ● ●
● ● ●
三角形全等
判定公理:三边对应相等的两个三角形全等(SSS)
公理:两边及其夹角对应相等的两个三角形全等(SAS)
公理:两角及其夹边对应相等的两个三角形全等(ASA)
性质公理:全等三角形的对应边、对应角相等.
你能用上面的公理证明下面的推论吗?
推论:两角及其中一角的对应边相等的两个三角形全等(AAS)
命题的证明
证明:
∵ ∠A=∠A′,∠C=∠C′(已知)∴∠B=∠B′(三角形内角和定理)
在△ABC与△A′B′C′中
∵ ∠A=∠A′ (已知),
AB=A′B′(已知),
∠B=∠B′ (已证),
∴ △ABC≌△A′B′C′(ASA).
A
B
C
A′
B′
C′
●
●
● ●
● ●
已知:如图,在△ABC和△A′B′C′中, ∠A=∠A′, ∠C=∠C′, AB=A′B′.
求证:△ABC≌△A′B′C′.
几何的三种语言
回顾与思考
推论:
两角及其一角的对边对应相等的两个三角形全等(AAS).
在△ABC与△A′B′C′中
∵∠A=∠A′
∠C=∠C′
AB=A′B′
∴△ABC≌△A′B′C′(AAS).
A
B
C
A′
B′
C′
●
●
● ●
● ●
证明后的结论,以后可以直接运用.
证明等腰三角形的性质
证明:等腰三角形的两个底角相等
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
证明:
作顶角的平分线AD. 在△BAD和△CAD中,
AB=AC ( 已知 ),
∠ BAD= ∠ CAD ( 辅助线作法 ),
AD=AD (公共边)
∴ △BAD ≌ △CAD (SAS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
A
B
C
D
作顶角的平分线
证明等腰三角形的性质
证明:等腰三角形的两个底角相等
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
证明:作底边中线AD.
在△BAD和△CAD中,
AB=AC ( 已知 ),
BD=CD ( 辅助线作法 ),
AD=AD (公共边) ,
∴ △BAD ≌ △CAD (SSS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
A
B
C
D
作底边中线
证明等腰三角形的性质
证明:等腰三角形的两个底角相等
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
证明:作底边高线AD.
在Rt△BAD和△RtCAD中,
AB=AC ( 已知 ),
AD=AD (公共边) ,
∴ Rt △BAD ≌ Rt △CAD (HL).
∴ ∠ B= ∠C (全等三角形的对应角相等).
A
B
C
D
作底边的高线
推论: 等腰三角形顶角的平分线、底边上的中线、底边上的高线互相重合(三线合一).
A
C
B
D
1
2
做一做P3
3
1、等腰三角形的顶角的平分线,既是底边上
的中线,又是底边上的高。
应用格式:∵AB=AC ∠1=∠2(已知)
∴BD=DC AD⊥BC(等腰三角形三线合一)
2、等腰三角形的底边上中线,既是底边上的高,又是
顶角平分线。
应用格式:∵AB=AC BD=DC (已知)
∴AD⊥BC ∠1=∠2 (等腰三角形三线合一)
3、等腰三角形的底边上的高,既是底
边上的中线,又是顶角平分线。
应用格式:∵AB=AC AD⊥BC (已知)
∴BD=DC ∠1=∠2 (等腰三角形三线合一)
A
C
B
D
1
2
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高,看看它们是否重合?
不重合!
三线合一
“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高
练习
1、已知:在△ABC中,AB=AC,∠A=80。求∠C和∠B的度数.
解:
结论:
在等腰三角形中,已知一个角,可以求另外两个角.
∵ AB=AC,
∴ ∠C=∠B( 等边对等角)
∵ ∠A+∠B +∠C=180。(三角形内角和等于180。)
∠A=80。
∴ ∠B=∠C=50。
练习
2、已知△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
A
B
C
D
解: ∵ AB=AC,(已知)
∴ ∠ABC=∠C (等边对等角)
∵ BD=BC=AD, (已知)
∴ ∠C=∠BDC (等边对等角)
∠A=∠ABD
设∠A=x°,则∠ABD= x°,
∠BDC=2 x°, ∠C=2 x°,
X°
X°
2X°
2X°
根据题意得:x+2x+2x=180
x=36
即∠A=36°∠ABC =∠ACB=72°
练习
3、已知AD⊥ BC,试找出等腰三角形ABC (AB=AC)中,存在相等关系的量.
C
B
D
A
1
2
∠B=∠C
∠1=∠2
∠BDA=∠CDA=90°
BD=CD
练习
4、填空:在△ABC中,AB=AC, D 在BC上,
(1)如果AD⊥BC,那么∠BAD = ∠______,
BD = ______.
(2)如果∠BAD= ∠CAD,那么AD⊥___, BD = ___.
(3)如果BD=CD,那么∠BAD =∠ _____, AD⊥___,
∠ADB =∠ _____=___°
D
CAD
CD
BC
CD
CAD
BC
ADC
90
练习
5、在三角形ABC中,AB=AC,且AD ⊥BC,已知BD=2cm,求DC=___cm, BC=___cm?
C
B
D
A
1
2
∵ AB=AC ,AD ⊥BC(已知)
∴BD=CD(等腰三角形的高与底边上的中线重合)
即(等腰三角形三线合一)
∵BD=2cm(已知)
∴CD=2cm
课堂小结
通过本节课的学习,你有哪些收获?
定理:等边对等角
推论:“三线合一”
常用来证明两角相等,求等腰三角形各角的度数.
研究等腰三角形的有关问题时“三线”是常用的辅助线.
等 腰 三 角 形
课后思考
建筑工人在盖房子时,用一块等腰三
角板放在梁上,从顶点系一重物,如果系
重物的绳子正好经过三角板底边中点,就
说房梁是水平
的,你知道其中
反映了什么数学
原理?
感谢您的聆听
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
