沪科版(2012)初中数学八年级上册 11.2 图形在坐标系中的平移 课件(20张)
文档属性
| 名称 | 沪科版(2012)初中数学八年级上册 11.2 图形在坐标系中的平移 课件(20张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 136.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 19:44:10 | ||
图片预览






文档简介
11.2 图形在坐标系中的平移
复 习
1)什么叫平移?
2)图形平移的性质是什么?
在平面内,把一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移。
1.新图形与原图形形状和大小不变,但位置改变。
2.对应点的连线平行且相等。
探索点的平移与坐标变化间的关系
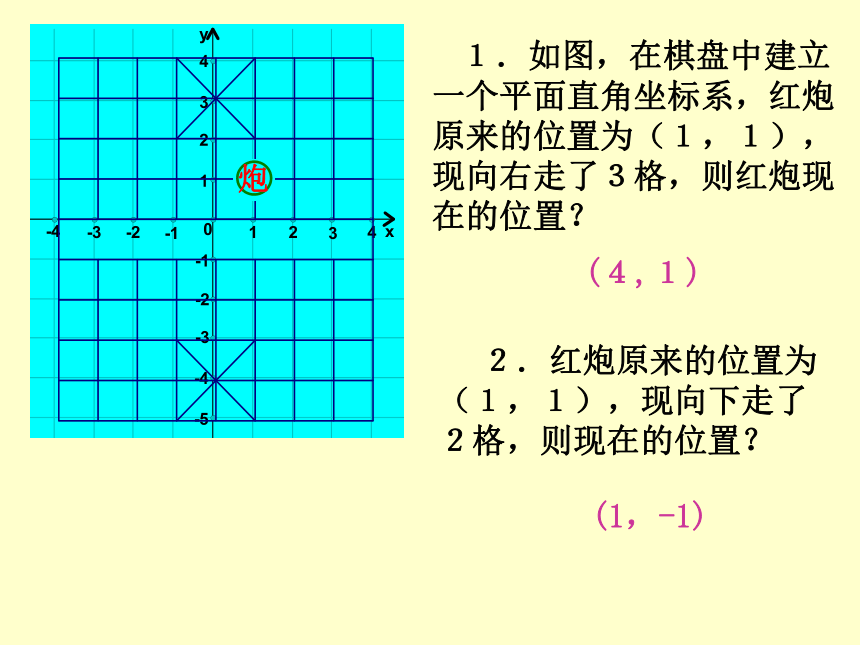
1.如图,在棋盘中建立一个平面直角坐标系,红炮原来的位置为(1,1),现向右走了3格,则红炮现在的位置?
2.红炮原来的位置为(1,1),现向下走了2格,则现在的位置?
(4,1)
(1,-1)
A1.
A.
.A”
A2.
.A’
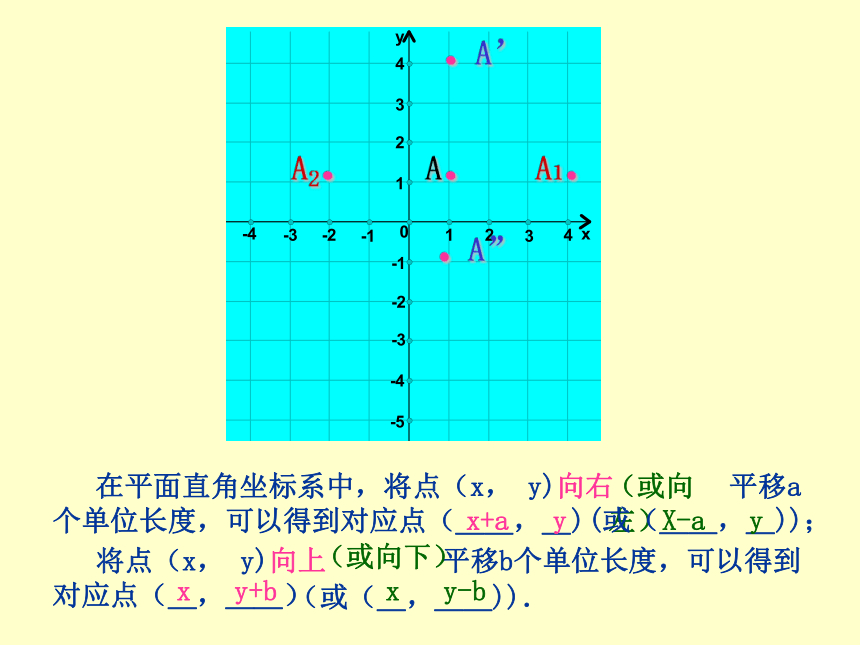
在平面直角坐标系中,将点(x, y)向右 平移a
个单位长度,可以得到对应点(__,_)
(或向左)
x+a y
(或(__,_));
将点(x, y)向上 平移b个单位长度,可以得到对应点(_,__)
x y+b
(或(_,__)).
X-a y
(或向下)
x y-b
练习
1、点P(2,-1)向左平移3个单位长度得点Q的坐标为 .
2、点P(2,-1)向上平移2个单位长度得点Q的坐标为 .
3、点P(2,-1)向右平移3个单位长度,再向下平移2个单位长度得点Q的坐标为 .
(-1 , -1)
( 2 , 1 )
(5 , -3)
探索图形的平移与点的坐标变化的关系
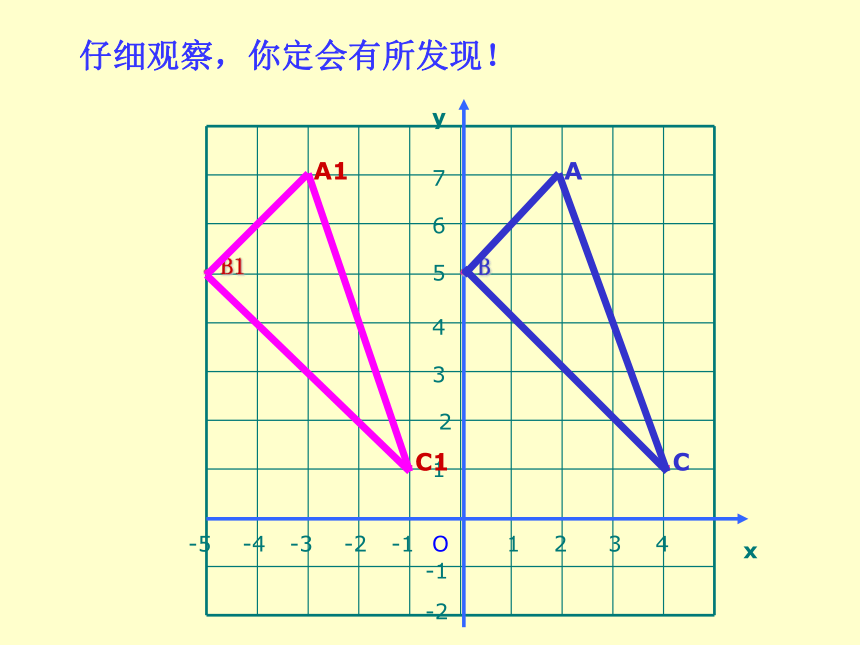
例 如图,三角形ABC在坐标平面内平移后得到新图形三角形A1B1C1.
(1)移动的方向和距离怎样?
观察:
(2)写出三角形ABC与三角形A1B1C1各顶点坐标.比较对应点坐标,看有怎样的变化?
O
1
2
3
4
1
2
3
4
-1
-2
-3
-4
-1
-2
.A
.C1
仔细观察,你定会有所发现!
y
x
.B1
-5
7
6
5
.A1
.B
.C
(3)如果三角形ABC向下平移2个单位,得到三角形A2B2C2.写出这时个顶点坐标,比较两者对应点坐标,看有怎样的变化?
O
1
2
3
4
1
2
3
4
-1
-2
-3
-4
-1
-2
.A
.C2
仔细观察,你定会有所发现!
y
x
.B2
-5
7
6
5
.B
.C
.A2
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
原图形上的点(x,y)
向左平移a个单位
原图形上的点(x,y)
(x+a,y)
(x-a,y)
向上平移b个单位
原图形上的点(x,y)
向下平移b个单位
原图形上的点(x,y)
(x,y+b)
(x,y-b)
总结规律1:图形平移与点的坐标变化
间的关系:
.A
.A1
思考:从A位置移到A1位置,应该如何平移得到?
A(x,y)
A1(x+2,y-3)
O
1
2
3
4
1
2
3
4
-1
-2
-3
-4
-1
-2
.A
.C1
课本P12例题
y
x
.B1
-5
7
6
5
.A1
.B
.C
练习
1、点A(1,1)是由(-2,1)向__移动__个单位长度得到的.
2、点A(1,1)是由(1,5)向__移动__个单位长度得到的.
3、点A(1,1)是由(5,-2)向__移动__个单位长度,向__移动__个单位长度得到的.
(1)横坐标变化,纵坐标不变:
向右平移a个单位
(x,y)
(x+a,y)
图形上点的坐标变化与图形平移间的关系
向左平移a个单位
(x,y)
(x-a,y)
向上平移b个单位
(x,y)
(x,y+b)
向下平移b个单位
(x,y)
(x,y-b)
(2)横坐标不变,纵坐标变化:
总结规律2:
4、线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为________.
(1,2)
x
y
0
1
4
2
3
-4
-1
-3
-2
1
4
2
3
-1
-2
-3
5、有相距5个单位的两点 A(-3,a),B(b,4),
AB//x轴,则a= ___ ,b= _ __ .
A
B
4
2或-8
B
小结
收获了什么?
1、知道了在平面直角坐标系内,将点
P(x,y)向左、右、上、下平移a 个
单位长度后,对应点的坐标变化情况.
2、将图形平移时就是将关键点进行平
移,再顺次连接各关键点.
小结
P(x, y)
P(x, y-b)
P(x, y+b)
向上平移
个单位
b
向下平移
个单位
b
P(x-a, y)
P(x+a, y)
向右平移
a个单位
向左平移
a个单位
复 习
1)什么叫平移?
2)图形平移的性质是什么?
在平面内,把一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移。
1.新图形与原图形形状和大小不变,但位置改变。
2.对应点的连线平行且相等。
探索点的平移与坐标变化间的关系
1.如图,在棋盘中建立一个平面直角坐标系,红炮原来的位置为(1,1),现向右走了3格,则红炮现在的位置?
2.红炮原来的位置为(1,1),现向下走了2格,则现在的位置?
(4,1)
(1,-1)
A1.
A.
.A”
A2.
.A’
在平面直角坐标系中,将点(x, y)向右 平移a
个单位长度,可以得到对应点(__,_)
(或向左)
x+a y
(或(__,_));
将点(x, y)向上 平移b个单位长度,可以得到对应点(_,__)
x y+b
(或(_,__)).
X-a y
(或向下)
x y-b
练习
1、点P(2,-1)向左平移3个单位长度得点Q的坐标为 .
2、点P(2,-1)向上平移2个单位长度得点Q的坐标为 .
3、点P(2,-1)向右平移3个单位长度,再向下平移2个单位长度得点Q的坐标为 .
(-1 , -1)
( 2 , 1 )
(5 , -3)
探索图形的平移与点的坐标变化的关系
例 如图,三角形ABC在坐标平面内平移后得到新图形三角形A1B1C1.
(1)移动的方向和距离怎样?
观察:
(2)写出三角形ABC与三角形A1B1C1各顶点坐标.比较对应点坐标,看有怎样的变化?
O
1
2
3
4
1
2
3
4
-1
-2
-3
-4
-1
-2
.A
.C1
仔细观察,你定会有所发现!
y
x
.B1
-5
7
6
5
.A1
.B
.C
(3)如果三角形ABC向下平移2个单位,得到三角形A2B2C2.写出这时个顶点坐标,比较两者对应点坐标,看有怎样的变化?
O
1
2
3
4
1
2
3
4
-1
-2
-3
-4
-1
-2
.A
.C2
仔细观察,你定会有所发现!
y
x
.B2
-5
7
6
5
.B
.C
.A2
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
原图形上的点(x,y)
向左平移a个单位
原图形上的点(x,y)
(x+a,y)
(x-a,y)
向上平移b个单位
原图形上的点(x,y)
向下平移b个单位
原图形上的点(x,y)
(x,y+b)
(x,y-b)
总结规律1:图形平移与点的坐标变化
间的关系:
.A
.A1
思考:从A位置移到A1位置,应该如何平移得到?
A(x,y)
A1(x+2,y-3)
O
1
2
3
4
1
2
3
4
-1
-2
-3
-4
-1
-2
.A
.C1
课本P12例题
y
x
.B1
-5
7
6
5
.A1
.B
.C
练习
1、点A(1,1)是由(-2,1)向__移动__个单位长度得到的.
2、点A(1,1)是由(1,5)向__移动__个单位长度得到的.
3、点A(1,1)是由(5,-2)向__移动__个单位长度,向__移动__个单位长度得到的.
(1)横坐标变化,纵坐标不变:
向右平移a个单位
(x,y)
(x+a,y)
图形上点的坐标变化与图形平移间的关系
向左平移a个单位
(x,y)
(x-a,y)
向上平移b个单位
(x,y)
(x,y+b)
向下平移b个单位
(x,y)
(x,y-b)
(2)横坐标不变,纵坐标变化:
总结规律2:
4、线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为________.
(1,2)
x
y
0
1
4
2
3
-4
-1
-3
-2
1
4
2
3
-1
-2
-3
5、有相距5个单位的两点 A(-3,a),B(b,4),
AB//x轴,则a= ___ ,b= _ __ .
A
B
4
2或-8
B
小结
收获了什么?
1、知道了在平面直角坐标系内,将点
P(x,y)向左、右、上、下平移a 个
单位长度后,对应点的坐标变化情况.
2、将图形平移时就是将关键点进行平
移,再顺次连接各关键点.
小结
P(x, y)
P(x, y-b)
P(x, y+b)
向上平移
个单位
b
向下平移
个单位
b
P(x-a, y)
P(x+a, y)
向右平移
a个单位
向左平移
a个单位
