冀教版初中数学八年级上册13.3 全等三角形的判定 课件(23张)
文档属性
| 名称 | 冀教版初中数学八年级上册13.3 全等三角形的判定 课件(23张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 331.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 19:26:39 | ||
图片预览



文档简介
13.3 全等三角形的判定(1)
小明家的衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明到玻璃店配一块回来,请你说说小明该怎么办?
带着另一块玻璃去吗?有没有更简单的办法?
想一想
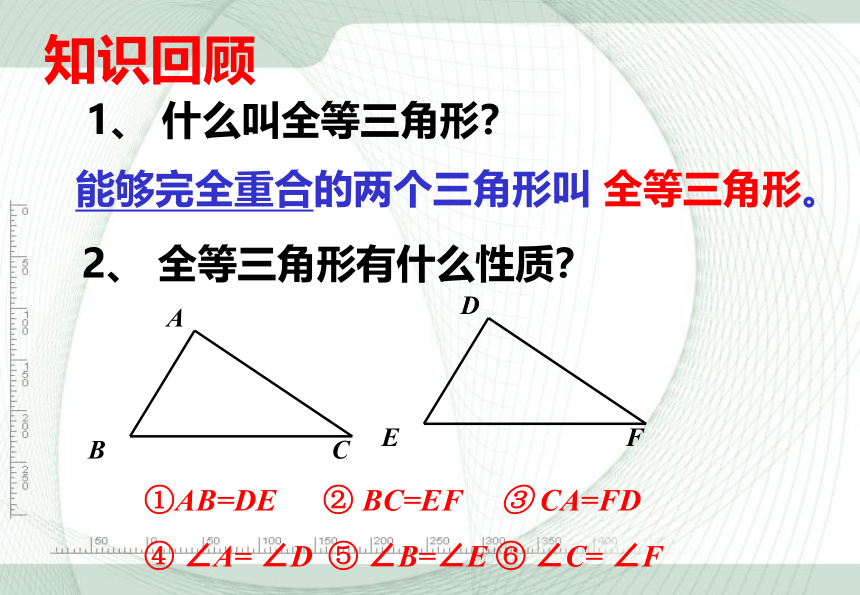
①AB=DE ② BC=EF ③ CA=FD
④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F
1、 什么叫全等三角形?
能够完全重合的两个三角形叫 全等三角形。
2、 全等三角形有什么性质?
知识回顾
A
B
C
D
E
F
A
B
C
D
E
F
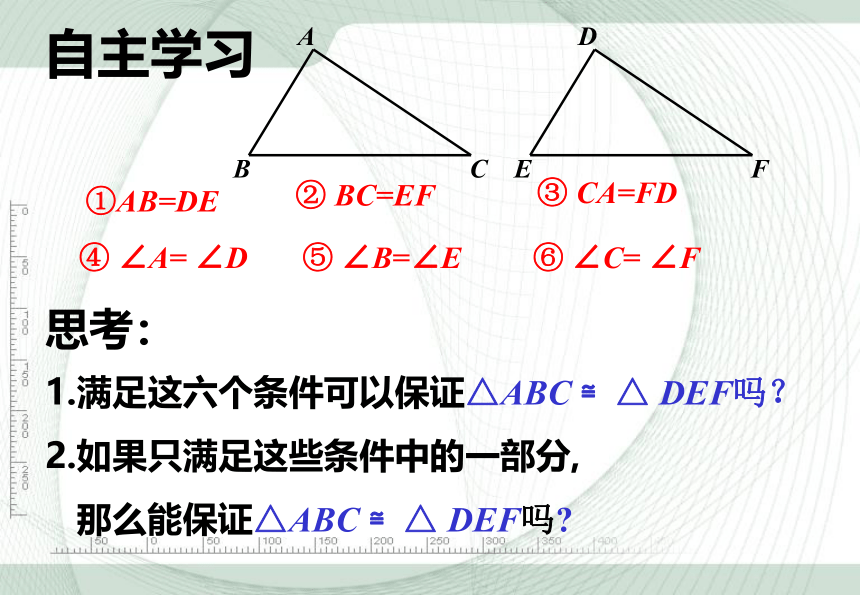
①AB=DE
③ CA=FD
② BC=EF
④ ∠A= ∠D
⑤ ∠B=∠E
⑥ ∠C= ∠F
1.满足这六个条件可以保证△ABC ≌△ DEF吗?
2.如果只满足这些条件中的一部分,
那么能保证△ABC ≌△ DEF吗?
思考:
自主学习
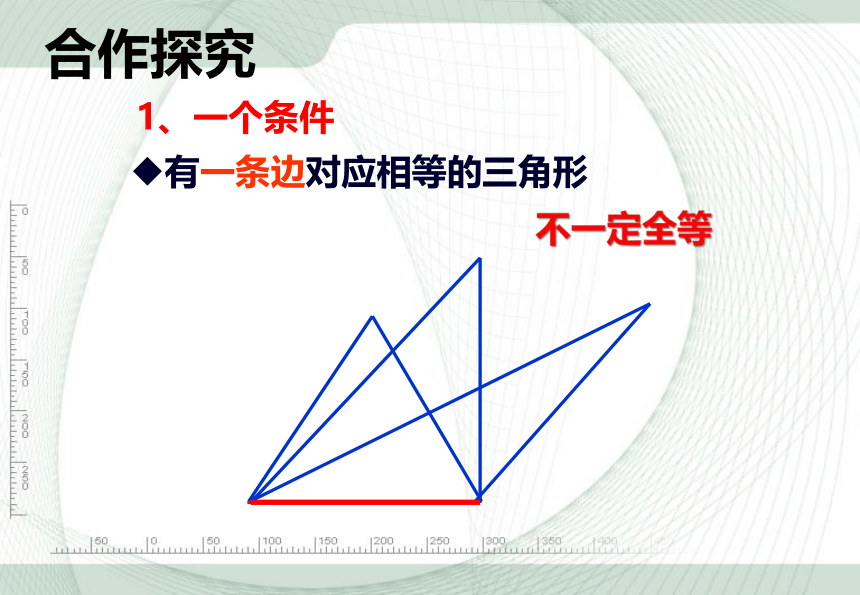
1、一个条件
有一条边对应相等的三角形
不一定全等
合作探究
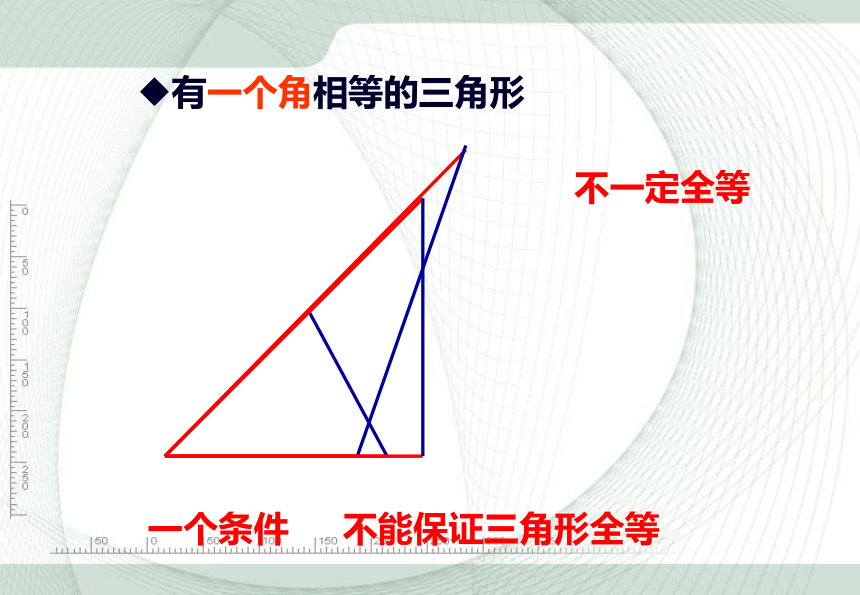
有一个角相等的三角形
不一定全等
一个条件
不能保证三角形全等
②两边;
③两角。
①一边一角;
如果满足两个条件,你能说出有哪几种可能的情况?
思考:
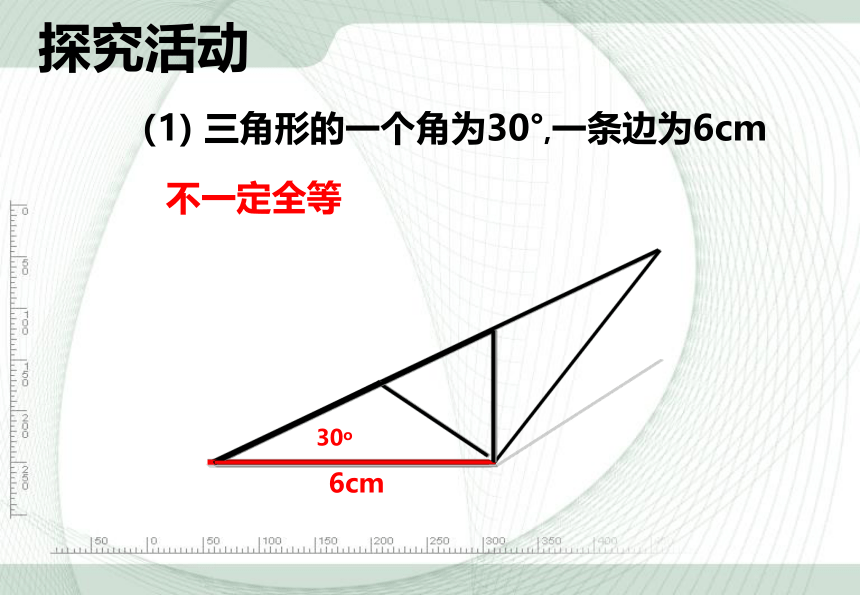
(1) 三角形的一个角为30°,一条边为6cm
30o
6cm
不一定全等
探究活动
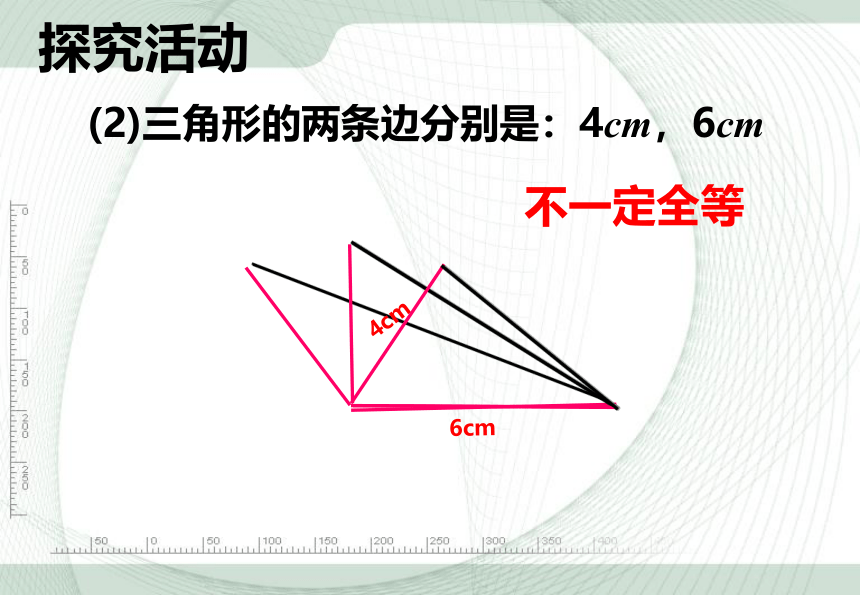
(2)三角形的两条边分别是:4cm,6cm
不一定全等
4cm
6cm
探究活动
(3)三角形的两个角分别是:30°,60°
300
60o
60o
60o
不一定全等
结论:
有两个条件分别相等不能
保证三角形全等
探究活动
②三边;
③两边一角;
④两角一边。
如果满足三个条件,你能说出有哪几种可能的情况?
思考:
①三角;
(1)已知三角形的三个角分别为30°、60°、90°
90o
90o
90o
三个内角分别相等的三角形不一定全等。
60o
300
60o
60o
探究活动
3、三个条件
结论
(1)已知三角形三条边分别是 3cm,4cm,5cm,画出这个三角形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?
探究新知
(2)如果三角形三条边分别是 4cm,5cm,7cm,上述的结论还成立吗?
(1)已知三角形三条边分别是 3cm,4cm,5cm,画出这个三角形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?
(2)如果三角形三条边分别是 4cm,5cm,7cm,上述的结论还成立吗?
边边边公理
如果两个三角形三边对应相等,
那么两个三角形全等.
简写成 “边边边” 或“ SSS ”
小明只要把三角形的每条边的长度量好,买回来的玻璃就会与原来的一样了。
1.用四根木条钉成一个四边形框架,你能把它拉变形吗?
2.用三根木条钉成一个三角形框架,你能把它拉变形吗?
三角形具有稳定性
一起探究
A
B
C
E
F
G
ABC ≌ EFG
AB=EF
BC=FG
AC=EG
(SSS)
几何语言:
在△ABC和△ EFG中
∴
已知: 如图,AC=AD ,BC=BD.
求证: △ACB ≌ △ADB.
A
B
C
D
证明:
在△ACB 和 △ADB中
AC = A D
BC = BD
A B = A B
∴△ACB≌△ADB
(SSS)
例1:
(已知)
(已知)
(公共边)
已知: 如图,AC=AD ,BC=BD.
求证: ∠C=∠D.
A
B
C
D
证明:
在△ACB 和 △ADB中
AC = A D
BC = BD
A B = A B
∴△ACB≌△ADB
(SSS)
连结AB
∴∠C=∠D.
(全等三角形对应角相等)
例2:
(已知)
(已知)
(公共边)
已知: 如图,点B、E、C、F在同一直线上 ,
AB = DE ,AC = DF ,BE = CF .
求证: ∠ A =∠ D
C
A
B
D
F
E
证明:
∴ △ABC ≌ △DEF ( SSS )
在△ABC 和△DEF中
AB = DE
AC = DF
BC = EF
(已知)
(已证)
∴ ∠ A =∠ D
(全等三角形的对应角相等)
∵ BE = CF
∴ BC = EF
∴ BE+EC = CF+CE
(等式性质)
例3:
(已知)
1、准备条件:证全等时要用的间接条件要先证好;
2、三角形全等书写三步骤:
(1)写出在哪两个三角形中
(2)摆出三个条件用大括号括起来
(3)写出全等结论
证明的书写步骤:
归纳
1、已知:AB=AC,AE=AD,BD=CE
求证:△AEB ≌ △ ADC
C
A
B
D
E
当堂练习
2、如图, △ABC 是钢架,AB = AC ,
AD是连结点A与BC中点D的支架.
求证: AD ⊥ BC
A
C
D
1
2
B
练习
课堂小结
三边分别相等的两个三角形全等,
简称“边边边”(即SSS);
3.找条件时要充分利用已知
(包括图形中隐含的条件,如公共边等);
4.书写格式:①准备条件;
②三角形全等书写的三步骤。
2.三角形具有稳定性
小明家的衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明到玻璃店配一块回来,请你说说小明该怎么办?
带着另一块玻璃去吗?有没有更简单的办法?
想一想
①AB=DE ② BC=EF ③ CA=FD
④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F
1、 什么叫全等三角形?
能够完全重合的两个三角形叫 全等三角形。
2、 全等三角形有什么性质?
知识回顾
A
B
C
D
E
F
A
B
C
D
E
F
①AB=DE
③ CA=FD
② BC=EF
④ ∠A= ∠D
⑤ ∠B=∠E
⑥ ∠C= ∠F
1.满足这六个条件可以保证△ABC ≌△ DEF吗?
2.如果只满足这些条件中的一部分,
那么能保证△ABC ≌△ DEF吗?
思考:
自主学习
1、一个条件
有一条边对应相等的三角形
不一定全等
合作探究
有一个角相等的三角形
不一定全等
一个条件
不能保证三角形全等
②两边;
③两角。
①一边一角;
如果满足两个条件,你能说出有哪几种可能的情况?
思考:
(1) 三角形的一个角为30°,一条边为6cm
30o
6cm
不一定全等
探究活动
(2)三角形的两条边分别是:4cm,6cm
不一定全等
4cm
6cm
探究活动
(3)三角形的两个角分别是:30°,60°
300
60o
60o
60o
不一定全等
结论:
有两个条件分别相等不能
保证三角形全等
探究活动
②三边;
③两边一角;
④两角一边。
如果满足三个条件,你能说出有哪几种可能的情况?
思考:
①三角;
(1)已知三角形的三个角分别为30°、60°、90°
90o
90o
90o
三个内角分别相等的三角形不一定全等。
60o
300
60o
60o
探究活动
3、三个条件
结论
(1)已知三角形三条边分别是 3cm,4cm,5cm,画出这个三角形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?
探究新知
(2)如果三角形三条边分别是 4cm,5cm,7cm,上述的结论还成立吗?
(1)已知三角形三条边分别是 3cm,4cm,5cm,画出这个三角形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?
(2)如果三角形三条边分别是 4cm,5cm,7cm,上述的结论还成立吗?
边边边公理
如果两个三角形三边对应相等,
那么两个三角形全等.
简写成 “边边边” 或“ SSS ”
小明只要把三角形的每条边的长度量好,买回来的玻璃就会与原来的一样了。
1.用四根木条钉成一个四边形框架,你能把它拉变形吗?
2.用三根木条钉成一个三角形框架,你能把它拉变形吗?
三角形具有稳定性
一起探究
A
B
C
E
F
G
ABC ≌ EFG
AB=EF
BC=FG
AC=EG
(SSS)
几何语言:
在△ABC和△ EFG中
∴
已知: 如图,AC=AD ,BC=BD.
求证: △ACB ≌ △ADB.
A
B
C
D
证明:
在△ACB 和 △ADB中
AC = A D
BC = BD
A B = A B
∴△ACB≌△ADB
(SSS)
例1:
(已知)
(已知)
(公共边)
已知: 如图,AC=AD ,BC=BD.
求证: ∠C=∠D.
A
B
C
D
证明:
在△ACB 和 △ADB中
AC = A D
BC = BD
A B = A B
∴△ACB≌△ADB
(SSS)
连结AB
∴∠C=∠D.
(全等三角形对应角相等)
例2:
(已知)
(已知)
(公共边)
已知: 如图,点B、E、C、F在同一直线上 ,
AB = DE ,AC = DF ,BE = CF .
求证: ∠ A =∠ D
C
A
B
D
F
E
证明:
∴ △ABC ≌ △DEF ( SSS )
在△ABC 和△DEF中
AB = DE
AC = DF
BC = EF
(已知)
(已证)
∴ ∠ A =∠ D
(全等三角形的对应角相等)
∵ BE = CF
∴ BC = EF
∴ BE+EC = CF+CE
(等式性质)
例3:
(已知)
1、准备条件:证全等时要用的间接条件要先证好;
2、三角形全等书写三步骤:
(1)写出在哪两个三角形中
(2)摆出三个条件用大括号括起来
(3)写出全等结论
证明的书写步骤:
归纳
1、已知:AB=AC,AE=AD,BD=CE
求证:△AEB ≌ △ ADC
C
A
B
D
E
当堂练习
2、如图, △ABC 是钢架,AB = AC ,
AD是连结点A与BC中点D的支架.
求证: AD ⊥ BC
A
C
D
1
2
B
练习
课堂小结
三边分别相等的两个三角形全等,
简称“边边边”(即SSS);
3.找条件时要充分利用已知
(包括图形中隐含的条件,如公共边等);
4.书写格式:①准备条件;
②三角形全等书写的三步骤。
2.三角形具有稳定性
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
