冀教版初中数学九年级上册 27.2 反比例函数的图象和性质 课件(31张)
文档属性
| 名称 | 冀教版初中数学九年级上册 27.2 反比例函数的图象和性质 课件(31张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 815.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 19:30:15 | ||
图片预览









文档简介
反比例函数的图象与性质
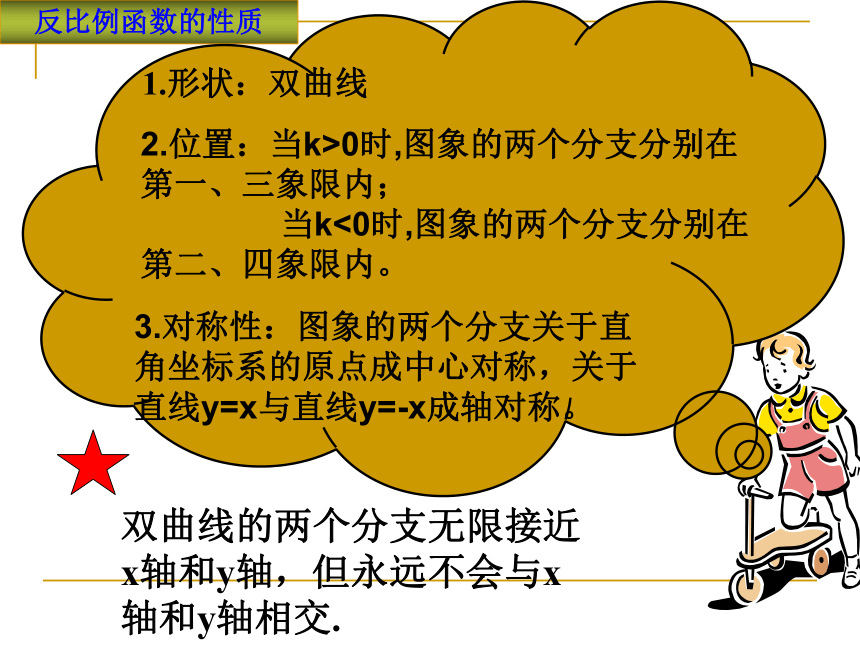
反比例函数的性质
双曲线的两个分支无限接近x轴和y轴,但永远不会与x轴和y轴相交.
1.形状:双曲线
2.位置:当k>0时,图象的两个分支分别在第一、三象限内;
当k<0时,图象的两个分支分别在第二、四象限内。
3.对称性:图象的两个分支关于直角坐标系的原点成中心对称,关于直线y=x与直线y=-x成轴对称。
复习题:
1.反比例函数 的图象经过点(-1,2),那么这个
反比例函数的解析式为 ,图象在第 象限,
它的图象关于 成中心对称.
2.反比例函数 的图象与正比例函数 的图象
交于点A(1,m),则m= ,反比例函数的解析式为
,
二、四
原点
2
观察反比例函数 的图象,回答下列问题:
(1)函数图象分别位于哪几个象限内?
第一、三象限内
在每一个象限内,y随x的增大而减小
(2)当x取什么值时,图象在第一象限?当x取什么值时,图象在第三象限?
(3)在每个象限内,随着x值的增大,y的值怎样变化?
当x>0时,图象在第一象限;当x<0时,图象在第三象限。
探究新知
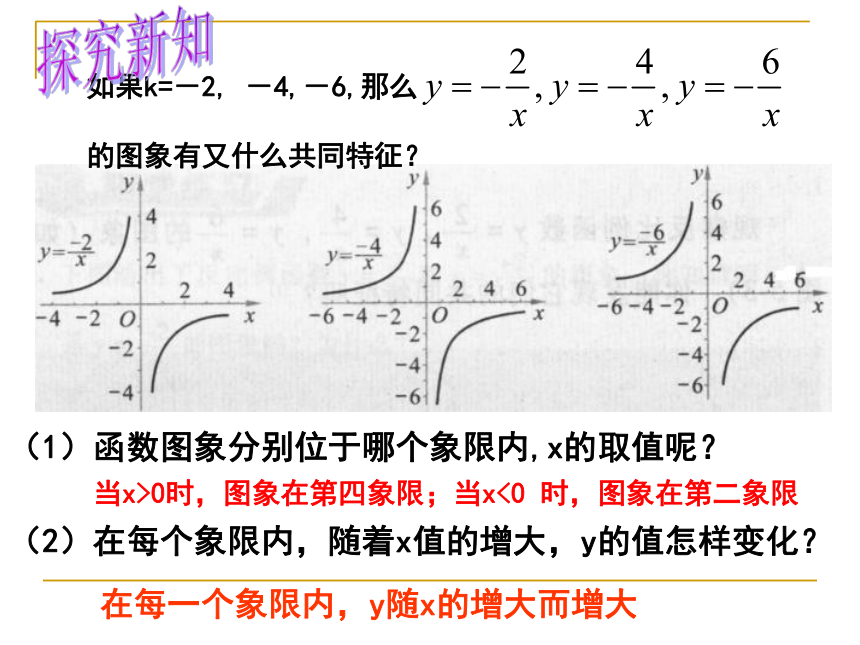
如果k=-2, -4,-6,那么
的图象有又什么共同特征?
(1)函数图象分别位于哪个象限内,x的取值呢?
(2)在每个象限内,随着x值的增大,y的值怎样变化?
在每一个象限内,y随x的增大而增大
当x>0时,图象在第四象限;当x<0 时,图象在第二象限
探究新知
当 时,在 内,
随 的增大而 .
O
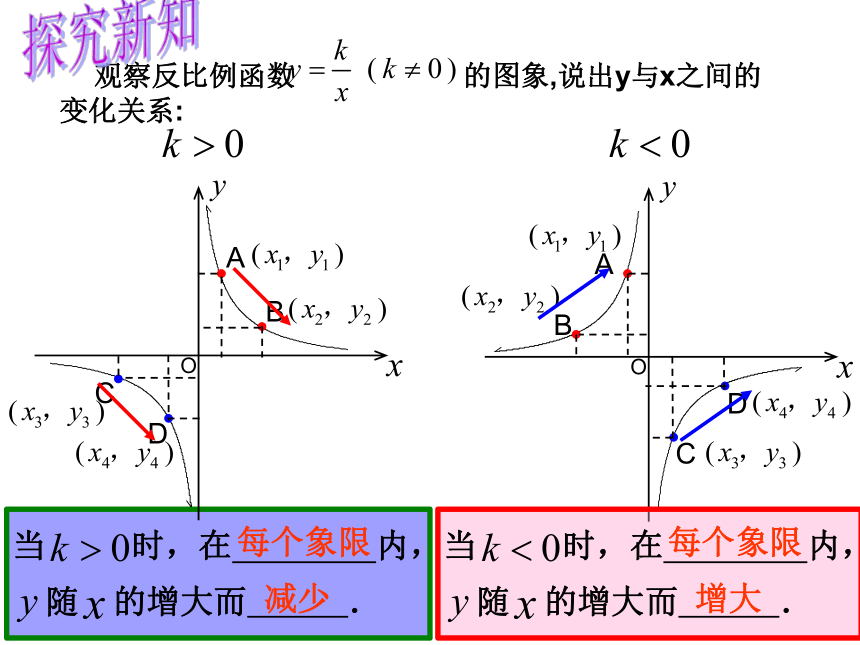
观察反比例函数 的图象,说出y与x之间的变化关系:
A
B
O
C
D
A
B
C
D
减少
每个象限
当 时,在 内,
随 的增大而 .
增大
每个象限
探究新知
1.下列函数中,其图象位于第一、三象限的有
____________;
在其所在的象限内,y随x的增大而增大的有
___________.
(1)(2)(3)
(4)
检测
结合函数图象和性质比较函数值或自变量的大小
例1 点A(-2,y1)与点B(-1,y2)都在反比例函数
的图象上,则y1与y2的大小关系为( )
A.y1<y2 B.y1>y2 C.y1=y2 D.无法确定
点A(2,y1)与点B( 1,y2)都在反比例函数
的图象上,则y1与y2的大小关系为( )
A.y1<y2 B.y1>y2 C.y1=y2 D.无法确定
变式一
变式一
A
B
代入法
性质法
图象法
你是怎么做的?还有别的做法吗?
点A(-2,y1)与点B( 1,y2)都在反比例函数
的图象上,则y1与y2的大小关系为( )
A.y1<y2 B.y1>y2 C.y1=y2 D.无法确定
变式二
B
设
是反比例函数
图象上的两点,若
则
A.y2C.y2>y1>0 D.y1>y2>0
之间的关系为( )
变式四
设
是反比例函数
图象上的两点,若
则
A.y1>y2 B.y1<y2
C.y2>0>y1 D.无法确定
之间的关系为( )
C
D
结合函数图象和性质比较函数值或自变量的大小
x2
y1
y2
x
y
O
x1
A
B
变式三
已知(x1,y1),(x2,y2),(x3,y3)是
反比例函数 图象上的三点,且y1>y2>y3>0,
变式六
则x1,x2,x3的大小关系是( )
A.x1x1>x2
C.x1>x2>x3 D.x1>x3>x2
若点A(-2,a),B(-1,b),C(1,c)在反比
例函数 的图象上,则a,b,c
大小关系为( )
A.a>b>c B.b>c>a C.c>a>b D.b>a>c
C
A
结合函数图象和性质比较函数值或自变量的大小
1
-1
O
-2
x
y
a
b
c
A
B
C
变式五
P(m,n)
A
o
y
x
B
P(m,n)
A
o
y
x
B
面积性质二
已知, 过点P作PA垂直x轴于A,PB垂直y轴于B点,则矩形OAPB的面积为多少?
K的几何意义
A
C
o
y
x
P
如图所示,A(x1 ,y1)、B(x2 ,y2)、
C(x3 ,y3)是函数y= 的图象在第一象限分支上的三个点,且 x1< x2 < x3 ,过A、B、C三点分别作坐标轴的垂线,得矩形ADOH、BEON、CFOP,它们的面积分别为S1、S2、S3,则下列结论中正确的是( )
1
A、S1B、S3 C、S2< S3< S1
D、S1= S2 = S3
D
P(m,n)
A
o
y
x
P(m,n)
A
o
y
x
面积性质一
K的几何意义
A.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3
B
A1
o
y
x
A
C
B1
C1
S2
A
如图,点A是反比例函数图象上的一点,自点A向y轴作垂线,垂足为T,已知S△AOT=3 则此函数的表达式为______
P(m,n)
A
o
y
x
P/
面积性质三
K的几何意义
A.S = 2 B.2C.S = 4 D.S>4
A
C
o
y
x
B
解:由上述性质(3)可知,
S△ABC = 2|k| = 4
C
如图,A,B是反比例函数 图像上的两个
点,并且关于原点O对称,过点A作x轴的垂线,过B作y轴的垂线,交点为C,则三角形ABC的面积为( )
小 结:
本节课我学到了……
我的疑惑……
1.用“>”或“<”填空:
已知 和 是反比例函数 的两对自变量与函数的对应值.若 ,则 .
>
>
火眼金睛:
2.已知( ),( ),( )是反比例函数
的图象上的三个点,并且 ,则
的大小关系是( )
(A) (B)
(C) (D)
3.已知( ),( ),( )是反比例函数
的图象上的三个点,则 的大小关系是
.
C
4. 如图点P 是反比例函数y= 4/x 的图象上的任意点,PA垂直于x轴,设三角形AOP的面积为S,则S=_____
2
5.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .
x
y
o
M
N
p
6.已知函数 的图象如下右图,则 y=kx-2 的图象大致是( )
x
x
y
y
y
o
o
x
o
x
y
o
(A)
(D)
(C)
x
y
o
(B)
D
7、已知反比例函数 ,y随x的增大而
减小,求a的值和表达式.
必做 P157 第三题
作业
A
B
C
E
O
F
x
y
x
如图,已知双曲线 (x>0)
经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k=____。
2
S⊿AOF = S矩形AOCB
S⊿AOF = S四边形EOBF =1
O
A
C
B
选作
正、反比例函数的图象与性质的比较:
正比例函数
反比例函数
解析式
增减性
直线
双曲线
k>0,一、三象限;
k<0,二、四象限.
k>0,y随x的增大而增大;
k>0,一、三象限;
k<0,二、四象限.
k<0,y随x的增大而减小.
k>0,在每个象限y随x的增大而减小;
k<0,在每个象限y随x的增大而增大.
图象
位置
再见
反比例函数的性质
双曲线的两个分支无限接近x轴和y轴,但永远不会与x轴和y轴相交.
1.形状:双曲线
2.位置:当k>0时,图象的两个分支分别在第一、三象限内;
当k<0时,图象的两个分支分别在第二、四象限内。
3.对称性:图象的两个分支关于直角坐标系的原点成中心对称,关于直线y=x与直线y=-x成轴对称。
复习题:
1.反比例函数 的图象经过点(-1,2),那么这个
反比例函数的解析式为 ,图象在第 象限,
它的图象关于 成中心对称.
2.反比例函数 的图象与正比例函数 的图象
交于点A(1,m),则m= ,反比例函数的解析式为
,
二、四
原点
2
观察反比例函数 的图象,回答下列问题:
(1)函数图象分别位于哪几个象限内?
第一、三象限内
在每一个象限内,y随x的增大而减小
(2)当x取什么值时,图象在第一象限?当x取什么值时,图象在第三象限?
(3)在每个象限内,随着x值的增大,y的值怎样变化?
当x>0时,图象在第一象限;当x<0时,图象在第三象限。
探究新知
如果k=-2, -4,-6,那么
的图象有又什么共同特征?
(1)函数图象分别位于哪个象限内,x的取值呢?
(2)在每个象限内,随着x值的增大,y的值怎样变化?
在每一个象限内,y随x的增大而增大
当x>0时,图象在第四象限;当x<0 时,图象在第二象限
探究新知
当 时,在 内,
随 的增大而 .
O
观察反比例函数 的图象,说出y与x之间的变化关系:
A
B
O
C
D
A
B
C
D
减少
每个象限
当 时,在 内,
随 的增大而 .
增大
每个象限
探究新知
1.下列函数中,其图象位于第一、三象限的有
____________;
在其所在的象限内,y随x的增大而增大的有
___________.
(1)(2)(3)
(4)
检测
结合函数图象和性质比较函数值或自变量的大小
例1 点A(-2,y1)与点B(-1,y2)都在反比例函数
的图象上,则y1与y2的大小关系为( )
A.y1<y2 B.y1>y2 C.y1=y2 D.无法确定
点A(2,y1)与点B( 1,y2)都在反比例函数
的图象上,则y1与y2的大小关系为( )
A.y1<y2 B.y1>y2 C.y1=y2 D.无法确定
变式一
变式一
A
B
代入法
性质法
图象法
你是怎么做的?还有别的做法吗?
点A(-2,y1)与点B( 1,y2)都在反比例函数
的图象上,则y1与y2的大小关系为( )
A.y1<y2 B.y1>y2 C.y1=y2 D.无法确定
变式二
B
设
是反比例函数
图象上的两点,若
则
A.y2
之间的关系为( )
变式四
设
是反比例函数
图象上的两点,若
则
A.y1>y2 B.y1<y2
C.y2>0>y1 D.无法确定
之间的关系为( )
C
D
结合函数图象和性质比较函数值或自变量的大小
x2
y1
y2
x
y
O
x1
A
B
变式三
已知(x1,y1),(x2,y2),(x3,y3)是
反比例函数 图象上的三点,且y1>y2>y3>0,
变式六
则x1,x2,x3的大小关系是( )
A.x1
C.x1>x2>x3 D.x1>x3>x2
若点A(-2,a),B(-1,b),C(1,c)在反比
例函数 的图象上,则a,b,c
大小关系为( )
A.a>b>c B.b>c>a C.c>a>b D.b>a>c
C
A
结合函数图象和性质比较函数值或自变量的大小
1
-1
O
-2
x
y
a
b
c
A
B
C
变式五
P(m,n)
A
o
y
x
B
P(m,n)
A
o
y
x
B
面积性质二
已知, 过点P作PA垂直x轴于A,PB垂直y轴于B点,则矩形OAPB的面积为多少?
K的几何意义
A
C
o
y
x
P
如图所示,A(x1 ,y1)、B(x2 ,y2)、
C(x3 ,y3)是函数y= 的图象在第一象限分支上的三个点,且 x1< x2 < x3 ,过A、B、C三点分别作坐标轴的垂线,得矩形ADOH、BEON、CFOP,它们的面积分别为S1、S2、S3,则下列结论中正确的是( )
1
A、S1
D、S1= S2 = S3
D
P(m,n)
A
o
y
x
P(m,n)
A
o
y
x
面积性质一
K的几何意义
A.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3
B
A1
o
y
x
A
C
B1
C1
S2
A
如图,点A是反比例函数图象上的一点,自点A向y轴作垂线,垂足为T,已知S△AOT=3 则此函数的表达式为______
P(m,n)
A
o
y
x
P/
面积性质三
K的几何意义
A.S = 2 B.2
A
C
o
y
x
B
解:由上述性质(3)可知,
S△ABC = 2|k| = 4
C
如图,A,B是反比例函数 图像上的两个
点,并且关于原点O对称,过点A作x轴的垂线,过B作y轴的垂线,交点为C,则三角形ABC的面积为( )
小 结:
本节课我学到了……
我的疑惑……
1.用“>”或“<”填空:
已知 和 是反比例函数 的两对自变量与函数的对应值.若 ,则 .
>
>
火眼金睛:
2.已知( ),( ),( )是反比例函数
的图象上的三个点,并且 ,则
的大小关系是( )
(A) (B)
(C) (D)
3.已知( ),( ),( )是反比例函数
的图象上的三个点,则 的大小关系是
.
C
4. 如图点P 是反比例函数y= 4/x 的图象上的任意点,PA垂直于x轴,设三角形AOP的面积为S,则S=_____
2
5.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .
x
y
o
M
N
p
6.已知函数 的图象如下右图,则 y=kx-2 的图象大致是( )
x
x
y
y
y
o
o
x
o
x
y
o
(A)
(D)
(C)
x
y
o
(B)
D
7、已知反比例函数 ,y随x的增大而
减小,求a的值和表达式.
必做 P157 第三题
作业
A
B
C
E
O
F
x
y
x
如图,已知双曲线 (x>0)
经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k=____。
2
S⊿AOF = S矩形AOCB
S⊿AOF = S四边形EOBF =1
O
A
C
B
选作
正、反比例函数的图象与性质的比较:
正比例函数
反比例函数
解析式
增减性
直线
双曲线
k>0,一、三象限;
k<0,二、四象限.
k>0,y随x的增大而增大;
k>0,一、三象限;
k<0,二、四象限.
k<0,y随x的增大而减小.
k>0,在每个象限y随x的增大而减小;
k<0,在每个象限y随x的增大而增大.
图象
位置
再见
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
