京改版八年级上册10.5可化为一元一次方程的分式方程及其应用(1)课件(23张)
文档属性
| 名称 | 京改版八年级上册10.5可化为一元一次方程的分式方程及其应用(1)课件(23张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 19:53:29 | ||
图片预览








文档简介
可化为一元一次方程的分式方程及其应用(1)
初二年级 数学
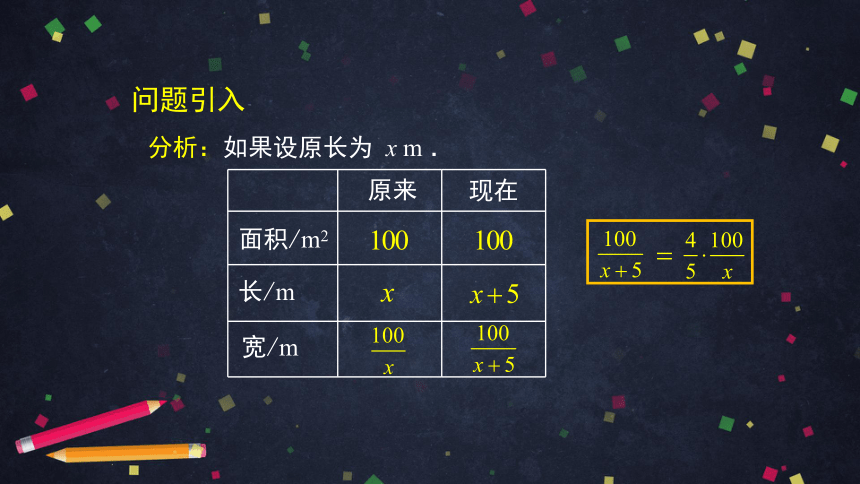
为了美化首都,北京市对元大都城墙遗址进行了大规模的修缮、扩建,使它成为一个“春有花、夏有荫、秋有果、冬有青”的景色怡人的公园.
园林设计者计划修建一个面积为100m2的长方形花坛.如果长方形花坛的面积100m2不变,把原长延长5m,宽变为原来的 ,那么原长是多少米?你能通过列方程解决吗?
问题引入
{5940675A-B579-460E-94D1-54222C63F5DA}
分析:如果设原长为 x m .
原来
现在
面积/m2
宽/m
长/m
问题引入
如: ; .
一元一次方程
方程左右两边都是整式.
方程里含有分式.
导出概念
二元一次方程
如: .
分式方程:
分母里含有未知数的方程叫做分式方程.
;
;
……
导出概念
判断下列哪个是分式方程?并说明理由.
(1) ;
(2) ;
(4) ;
(6) .
(3) ;
导出概念
(5) ;
(2)和(6)是分式方程.
对比:分式方程与整式方程的区别是什么?
(1) ;
(2) ;
——分母里含有未知数.
(6) .
导出概念
(5) ;
分式方程
整式方程
(4) ;
解下列方程:
(1) ;
(2) .
解法探究
解:(1) .
去分母,得
.
解这个方程,得
.
所以原方程的解是
.
在方程两边同乘6,得
.
解法探究
解这个方程,得
.
(2) .
去分母,得
.
在方程两边同乘 ,得
.
?
解法探究
所以原方程的解是
.
所以左边=右边.
因为左边 ,右边 .
把 分别代入原方程的左右两边检验:
(2) .
(1) ;
(2) .
两边同乘6
两边同乘
解分式方程时,方程两边同乘各分母的最简公分母,
通过去分母的方法,把分式方程转化为整式方程求解.
.
.
解法探究
例 解下列方程:
(1) ;
(2) .
例题讲解
解:(1) .
在方程两边同乘 ,得
.
去分母,得
.
解这个方程,得
.
分式方程
整式方程
去分母 转化
例题讲解
(1) .
所以原方程的解是
.
所以左边=右边 .
把 分别代入原方程的左右两边检验:
例题讲解
因为左边 ,右边 .
原方程可转化为
.
解:(2) .
分式方程
整式方程
去分母 转化
例题讲解
在方程两边同乘 ,得
.
去分母,得
.
解这个方程,得
.
思考: 不是原方程的解,它是哪个方程的解呢?
你发现了什么问题?
把 分别代入原方程的左右两边检验:
(2) .
分式方程中两个分母的值为零,这两个分式没有意义.
例题讲解
当 时,分母 , ,
分式方程
整式方程
检验:当 时,最简公分母 ,原方程中的分式无意义.
所以原方程无解.
例题讲解
.
解这个方程,得
.
分母 .
分式无意义.
方程左边 右边 .
.
(2) .
两边同乘
1 .比较解分数系数的一元一次方程和解分式方程有什么相同点,
有什么不同点?
相同点:通过去分母的方法求解.
不同点:
总结归纳
解分式方程:方程两边同乘各分母的最简公分母,它的值有可能
为零,求得的整式方程的解不一定是原方程的解,
必须通过检验来确定.
解分数系数的一元一次方程:方程两边同乘各分母的最小公倍数;
2 .解分式方程的一般步骤是什么?
(1)去分母:把分式方程两边同乘各分母的最简公分母,
转化为整式方程;
(2)解这个整式方程;
(4)确定分式方程的解.
(3)检验:
把所得的未知数的值代入方程的左右两边或最简公分母;
总结归纳
解方程
.
解:方程两边同乘 ,去分母,得
.
解这个方程,得
.
检验:当 时,方程左右两边相等.
所以原方程的解是 .
分式方程
整式方程
去分母 转化
巩固练习
3.解分式方程的基本思路和方法是“转化”,即
整式方程 ;
去分母
转化
分式方程
1.分式方程的定义:
分母中含有未知数的方程叫做分式方程;
4.检验是解分式方程的重要步骤.
课堂小结
2.类比分数系数的一元一次方程的求解过程,学习了分式方程的解法;
解下列方程:
(1) ;
(2) ;
(4) .
(3) ;
课后练习
祝同学们学习进步!
初二年级 数学
为了美化首都,北京市对元大都城墙遗址进行了大规模的修缮、扩建,使它成为一个“春有花、夏有荫、秋有果、冬有青”的景色怡人的公园.
园林设计者计划修建一个面积为100m2的长方形花坛.如果长方形花坛的面积100m2不变,把原长延长5m,宽变为原来的 ,那么原长是多少米?你能通过列方程解决吗?
问题引入
{5940675A-B579-460E-94D1-54222C63F5DA}
分析:如果设原长为 x m .
原来
现在
面积/m2
宽/m
长/m
问题引入
如: ; .
一元一次方程
方程左右两边都是整式.
方程里含有分式.
导出概念
二元一次方程
如: .
分式方程:
分母里含有未知数的方程叫做分式方程.
;
;
……
导出概念
判断下列哪个是分式方程?并说明理由.
(1) ;
(2) ;
(4) ;
(6) .
(3) ;
导出概念
(5) ;
(2)和(6)是分式方程.
对比:分式方程与整式方程的区别是什么?
(1) ;
(2) ;
——分母里含有未知数.
(6) .
导出概念
(5) ;
分式方程
整式方程
(4) ;
解下列方程:
(1) ;
(2) .
解法探究
解:(1) .
去分母,得
.
解这个方程,得
.
所以原方程的解是
.
在方程两边同乘6,得
.
解法探究
解这个方程,得
.
(2) .
去分母,得
.
在方程两边同乘 ,得
.
?
解法探究
所以原方程的解是
.
所以左边=右边.
因为左边 ,右边 .
把 分别代入原方程的左右两边检验:
(2) .
(1) ;
(2) .
两边同乘6
两边同乘
解分式方程时,方程两边同乘各分母的最简公分母,
通过去分母的方法,把分式方程转化为整式方程求解.
.
.
解法探究
例 解下列方程:
(1) ;
(2) .
例题讲解
解:(1) .
在方程两边同乘 ,得
.
去分母,得
.
解这个方程,得
.
分式方程
整式方程
去分母 转化
例题讲解
(1) .
所以原方程的解是
.
所以左边=右边 .
把 分别代入原方程的左右两边检验:
例题讲解
因为左边 ,右边 .
原方程可转化为
.
解:(2) .
分式方程
整式方程
去分母 转化
例题讲解
在方程两边同乘 ,得
.
去分母,得
.
解这个方程,得
.
思考: 不是原方程的解,它是哪个方程的解呢?
你发现了什么问题?
把 分别代入原方程的左右两边检验:
(2) .
分式方程中两个分母的值为零,这两个分式没有意义.
例题讲解
当 时,分母 , ,
分式方程
整式方程
检验:当 时,最简公分母 ,原方程中的分式无意义.
所以原方程无解.
例题讲解
.
解这个方程,得
.
分母 .
分式无意义.
方程左边 右边 .
.
(2) .
两边同乘
1 .比较解分数系数的一元一次方程和解分式方程有什么相同点,
有什么不同点?
相同点:通过去分母的方法求解.
不同点:
总结归纳
解分式方程:方程两边同乘各分母的最简公分母,它的值有可能
为零,求得的整式方程的解不一定是原方程的解,
必须通过检验来确定.
解分数系数的一元一次方程:方程两边同乘各分母的最小公倍数;
2 .解分式方程的一般步骤是什么?
(1)去分母:把分式方程两边同乘各分母的最简公分母,
转化为整式方程;
(2)解这个整式方程;
(4)确定分式方程的解.
(3)检验:
把所得的未知数的值代入方程的左右两边或最简公分母;
总结归纳
解方程
.
解:方程两边同乘 ,去分母,得
.
解这个方程,得
.
检验:当 时,方程左右两边相等.
所以原方程的解是 .
分式方程
整式方程
去分母 转化
巩固练习
3.解分式方程的基本思路和方法是“转化”,即
整式方程 ;
去分母
转化
分式方程
1.分式方程的定义:
分母中含有未知数的方程叫做分式方程;
4.检验是解分式方程的重要步骤.
课堂小结
2.类比分数系数的一元一次方程的求解过程,学习了分式方程的解法;
解下列方程:
(1) ;
(2) ;
(4) .
(3) ;
课后练习
祝同学们学习进步!
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
