京改版八年级上册11.1平方根(1)课件(37张)
文档属性
| 名称 | 京改版八年级上册11.1平方根(1)课件(37张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 19:53:33 | ||
图片预览



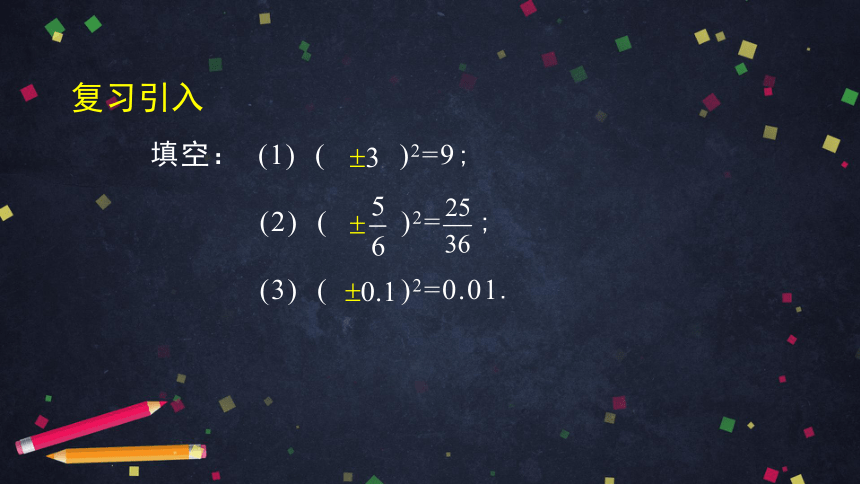
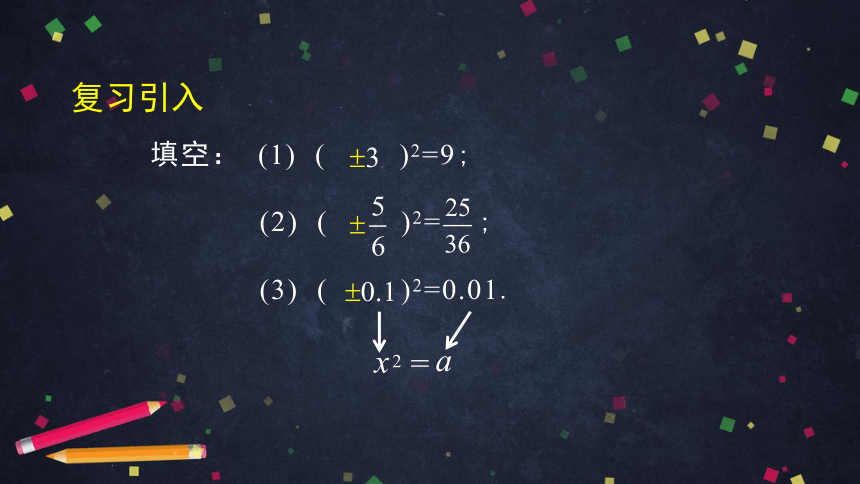






文档简介
平方根(1)
初二年级 数学
请思考:我们学习过哪几种运算?
加法
乘法
乘方
?
复习引入
减法
除法
口算:
(1) =
(2) =
(3) =
4;
0.25.
复习引入
;
填空: (1) ( )2=9;
(2) ( )2= ;
(3) ( )2=0.01.
复习引入
填空: (1) ( )2=9;
(2) ( )2= ;
(3) ( )2=0.01.
复习引入
x
a
2 =
一般地,如果一个数x 的平方等于a,那么这个数x 就叫做a 的平方根.
如果 x2=a,那么x 叫做a 的平方根.
探索新知
一般地,如果一个数x 的平方等于a,那么这个数x 就叫做a 的平方根.
4
因为 ,所以 是 的平方根.
探索新知
如果 x2=a,那么x 叫做a 的平方根.
已知
一个数
求
这个数
的平方
+6
36
平方
运算
已知
一个数
的平方
求
这个数
36
+6
归纳小结
已知
一个数
求
这个数
的平方
+6
36
平方
运算
已知
一个数
求
这个数的平方根
36
+6
归纳小结
开平方
运算
求一个数的平方根的运算叫做开平方.
开平方运算的结果是平方根.
探索新知
对比归纳
36
平方运算
开平方运算
互为逆运算
加法运算 减法运算
乘法运算 除法运算
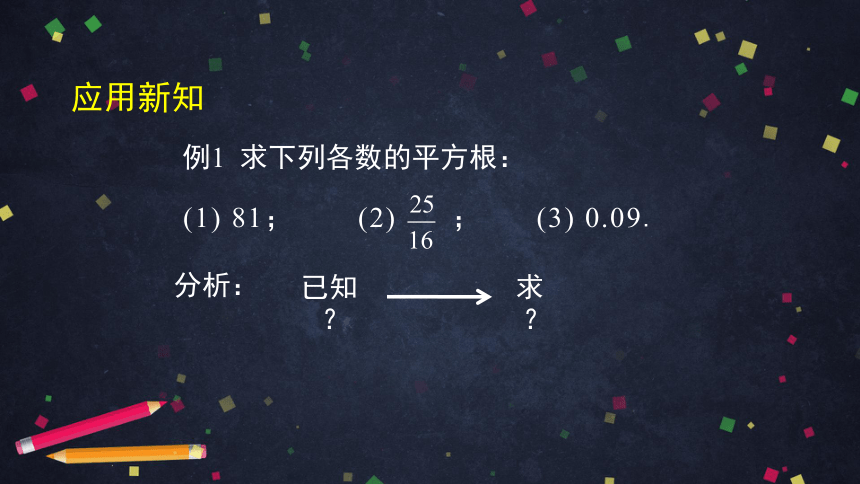
例1 求下列各数的平方根:
(1) 81; (2) ; (3) 0.09.
分析:
已知 求
?
?
应用新知
例1 求下列各数的平方根:
分析:
已知
一个数
求
这个数的
平方根
开平方
运算
应用新知
(1) 81; (2) ; (3) 0.09.
例1 求下列各数的平方根:
应用新知
(1) 81; (2) ; (3) 0.09.
解:(1)
81的平方根是?
( )2=81
例1 求下列各数的平方根:
81的平方根是
( )2=81
因为 ,
所以 ;
应用新知
(1) 81; (2) ; (3) 0.09.
解:(1)
例1 求下列各数的平方根:
应用新知
因为 ,
( )2=
所以 的平方根是 ;
(1) 81; (2) ; (3) 0.09.
解:(2)
例1 求下列各数的平方根:
应用新知
(1) 81; (2) ; (3) 0.09.
解:(3)
因为( )2=0.09,
所以0.09的平方根是 .
归纳小结
已知
一个数
这个数的
平方根
求出
平方运算
开平方运算
互为逆运算
例2 求满足下列条件的x的值:
应用新知
(1) ;
(2) .
应用新知
解:
(1) ;
例2 求满足下列条件的x的值:
应用新知
(2) .
例2 求满足下列条件的x的值:
解:
想一想
1.我们所学过的数都有平方根吗?
3. 它们的平方根有怎样的关系呢?
2. 如果有平方根,有几个?
有理数
正数
负数
零
有两个
互为相反数
的平方根是
81 的平方根是
0.09 的平方根是
有理数
正数
负数
零
有两个平方根
它们互为相反数
有理数
正数
负数
零
0 的平方根是?
0
有理数
正数
负数
零
0 的平方根是 0
有理数
正数
负数
零
0
只有一个平方根
有理数
正数
负数
零
有理数
正数
负数
零
没有平方根
任何有理数
的平方都是
非负数
有理数
正数
负数
零
没有平方根
有理数
正数
负数
零
没有平方根
有两个平方根
它们互为相反数
只有一个平方根
0
平方根的性质
例3 判断下列说法是否正确:
(1) 0的平方根是0;
(2) 1的平方根是1;
(3) 是4的平方根;
(4) 的平方根是 ;
(5) 的平方根是 .
应用新知
正确
错误
正确
错误
错误
总结回顾
1.平方根的概念和开平方运算:
一般地,如果一个数x 的平方等于a,那么这个数x 就叫做a 的平方根.
求一个数的平方根的运算叫做开平方.
如果 x2=a,那么x 叫做a 的平方根.
总结回顾
2.平方根的性质:
正数有两个平方根,它们互为相反数;
零的平方根是零;
负数没有平方根.
总结回顾
3.怎样求一个正数的平方根?
平方运算
开平方运算
互为逆运算
课后练习
1. 求下列各数的平方根:
(1) 64; (2) ; (3) 0.0016 ; (4) .
2. 求下列各式中x的值:
(1) ;
(2) .
祝同学们学习愉快!
初二年级 数学
请思考:我们学习过哪几种运算?
加法
乘法
乘方
?
复习引入
减法
除法
口算:
(1) =
(2) =
(3) =
4;
0.25.
复习引入
;
填空: (1) ( )2=9;
(2) ( )2= ;
(3) ( )2=0.01.
复习引入
填空: (1) ( )2=9;
(2) ( )2= ;
(3) ( )2=0.01.
复习引入
x
a
2 =
一般地,如果一个数x 的平方等于a,那么这个数x 就叫做a 的平方根.
如果 x2=a,那么x 叫做a 的平方根.
探索新知
一般地,如果一个数x 的平方等于a,那么这个数x 就叫做a 的平方根.
4
因为 ,所以 是 的平方根.
探索新知
如果 x2=a,那么x 叫做a 的平方根.
已知
一个数
求
这个数
的平方
+6
36
平方
运算
已知
一个数
的平方
求
这个数
36
+6
归纳小结
已知
一个数
求
这个数
的平方
+6
36
平方
运算
已知
一个数
求
这个数的平方根
36
+6
归纳小结
开平方
运算
求一个数的平方根的运算叫做开平方.
开平方运算的结果是平方根.
探索新知
对比归纳
36
平方运算
开平方运算
互为逆运算
加法运算 减法运算
乘法运算 除法运算
例1 求下列各数的平方根:
(1) 81; (2) ; (3) 0.09.
分析:
已知 求
?
?
应用新知
例1 求下列各数的平方根:
分析:
已知
一个数
求
这个数的
平方根
开平方
运算
应用新知
(1) 81; (2) ; (3) 0.09.
例1 求下列各数的平方根:
应用新知
(1) 81; (2) ; (3) 0.09.
解:(1)
81的平方根是?
( )2=81
例1 求下列各数的平方根:
81的平方根是
( )2=81
因为 ,
所以 ;
应用新知
(1) 81; (2) ; (3) 0.09.
解:(1)
例1 求下列各数的平方根:
应用新知
因为 ,
( )2=
所以 的平方根是 ;
(1) 81; (2) ; (3) 0.09.
解:(2)
例1 求下列各数的平方根:
应用新知
(1) 81; (2) ; (3) 0.09.
解:(3)
因为( )2=0.09,
所以0.09的平方根是 .
归纳小结
已知
一个数
这个数的
平方根
求出
平方运算
开平方运算
互为逆运算
例2 求满足下列条件的x的值:
应用新知
(1) ;
(2) .
应用新知
解:
(1) ;
例2 求满足下列条件的x的值:
应用新知
(2) .
例2 求满足下列条件的x的值:
解:
想一想
1.我们所学过的数都有平方根吗?
3. 它们的平方根有怎样的关系呢?
2. 如果有平方根,有几个?
有理数
正数
负数
零
有两个
互为相反数
的平方根是
81 的平方根是
0.09 的平方根是
有理数
正数
负数
零
有两个平方根
它们互为相反数
有理数
正数
负数
零
0 的平方根是?
0
有理数
正数
负数
零
0 的平方根是 0
有理数
正数
负数
零
0
只有一个平方根
有理数
正数
负数
零
有理数
正数
负数
零
没有平方根
任何有理数
的平方都是
非负数
有理数
正数
负数
零
没有平方根
有理数
正数
负数
零
没有平方根
有两个平方根
它们互为相反数
只有一个平方根
0
平方根的性质
例3 判断下列说法是否正确:
(1) 0的平方根是0;
(2) 1的平方根是1;
(3) 是4的平方根;
(4) 的平方根是 ;
(5) 的平方根是 .
应用新知
正确
错误
正确
错误
错误
总结回顾
1.平方根的概念和开平方运算:
一般地,如果一个数x 的平方等于a,那么这个数x 就叫做a 的平方根.
求一个数的平方根的运算叫做开平方.
如果 x2=a,那么x 叫做a 的平方根.
总结回顾
2.平方根的性质:
正数有两个平方根,它们互为相反数;
零的平方根是零;
负数没有平方根.
总结回顾
3.怎样求一个正数的平方根?
平方运算
开平方运算
互为逆运算
课后练习
1. 求下列各数的平方根:
(1) 64; (2) ; (3) 0.0016 ; (4) .
2. 求下列各式中x的值:
(1) ;
(2) .
祝同学们学习愉快!
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
