京改版八年级上册11.2立方根课件( 共45张ppt)
文档属性
| 名称 | 京改版八年级上册11.2立方根课件( 共45张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 886.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览









文档简介
立方根
初二年级 数学
问题引入
为了建造一个容积为343立方米,形状为正方体的蓄水池,它的棱长应取多少米?
棱长3=体积
343
?3=
问题引入
为了建造一个容积为343立方米,形状为正方体的蓄水池,它的棱长应取多少米?
问题引入
x
x3=343
为了建造一个容积为343立方米,形状为正方体的蓄水池,它的棱长应取多少米?
问题引入
x3=343
x2=343
x叫343的平方根
x叫343的立方根
平方根的定义
a 的平方根用符号“ ”表示.
如果 x?=a ,那么 x 叫做 a 的平方根.
一般地,如果一个数x的平方等于a ,那么
这个数x就叫做 a 的平方根.
回顾旧知
立方根的定义
一般地,如果一个数x的立方等于a ,那么
这个数x就叫做 a 的立方根.
学习新知
如果 x3=a ,那么 x 叫做a 的立方根.
因为 ,
所以 是 的立方根.
“a 的立方根” 记作:
读作:“三次根号a”
立方根的表示法
3
例如:“8的立方根” 记作:“ ”
3
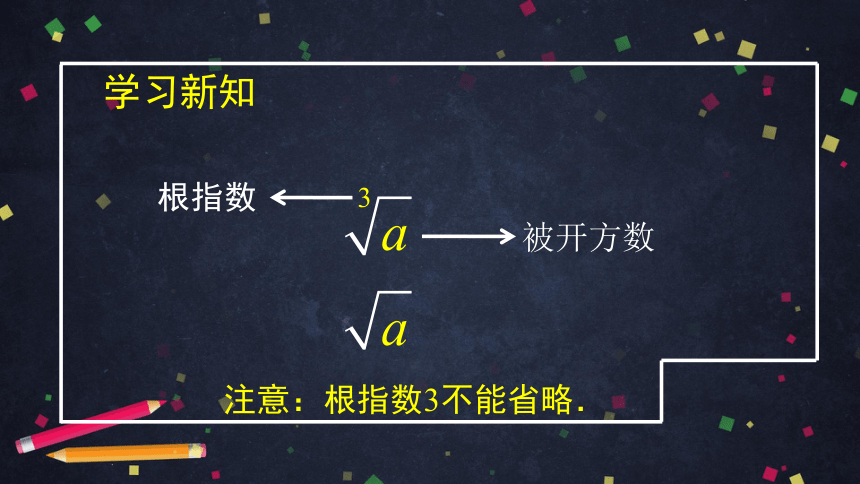
学习新知
注意:根指数3不能省略.
被开方数
根指数
3
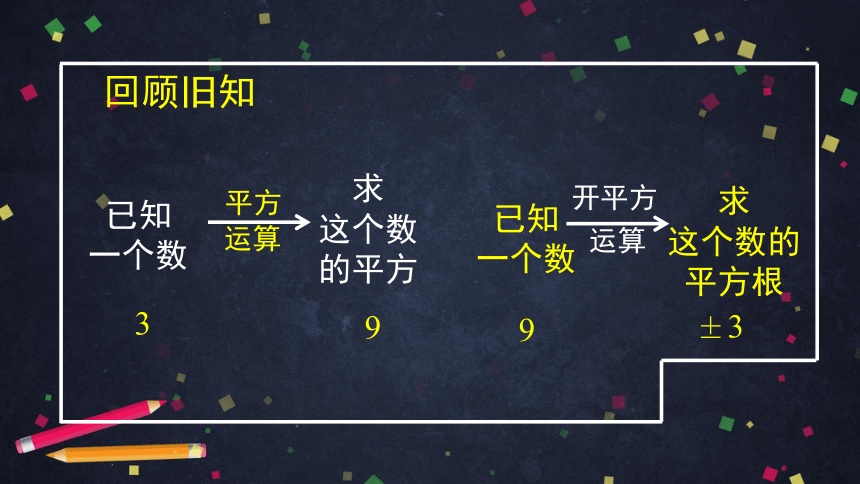
学习新知
9
已知
一个数
±3
求
这个数的平方根
开平方
运算
求
这个数
的平方
3
9
平方
运算
已知
一个数
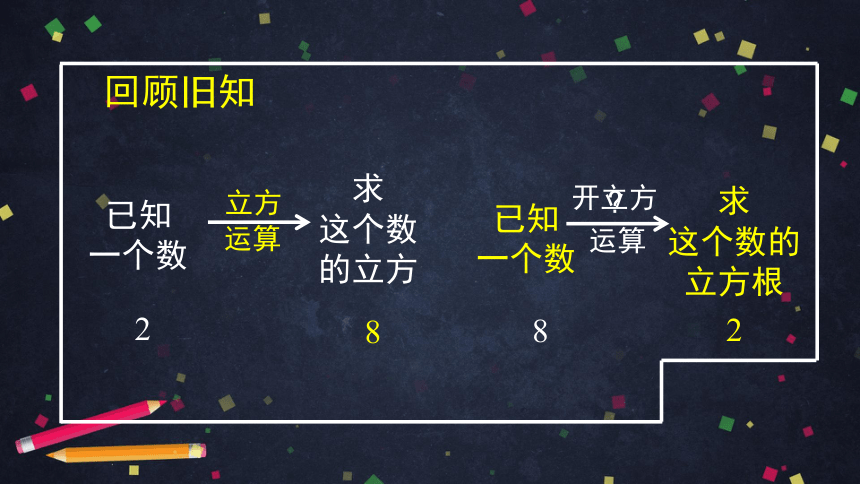
回顾旧知
已知
一个数
求
这个数的立方根
开立方
运算
求
这个数
的立方
立方
运算
已知
一个数
回顾旧知
2
8
8
2
?
求一个数的立方根的运算叫做开立方.
开立方运算的结果是立方根.
开立方运算 立方运算
互为
逆运算
学习新知
例1 求下列各数的立方根:
(1)27; (2) ;(3) ;(4)-0.001.
学以致用
例1 求下列各数的立方根:
(1)27;
解:
3=27,
( )
因为
所以 ,
3
27的立方根是
3
?
分析:
即
.
3
学以致用
例1 求下列各数的立方根:
(2) ;
( )
因为 ,
解:
的立方根是
所以 ,
,
即
.
3
学以致用
例1 求下列各数的立方根:
(3) ;
解:
( )
3= ,
所以 ,
的立方根是
因为
.
即
3
学以致用
例1 求下列各数的立方根:
(4) .
解:
3=-0.001,
( )
所以
-0.001的立方根是
-0.1,
-0.1
因为
.
即
3
学以致用
求一个数的立方根的方法
立方运算
开立方运算
互为
逆运算
归纳小结
求一个数的立方根的方法
归纳小结
正数有两个平方根,它们互为相反数;
负数没有平方根.
零的平方根是零;
平方根的性质
回顾旧知
1.一个正数有两个平方根,那么一个正数有几个
立方根?
想一想
2.负数没有平方根,那么负数有立方根吗?
回顾旧知
有一个
是个正数
的立方根是
8 的立方根是
的立方根是
正数
负数
零
观察归纳
的立方根是正数
正数
负数
零
观察归纳
0
正数
负数
零
观察归纳
的立方根是零
正数
负数
零
观察归纳
有一个
是个负数
的立方根是
-8 的立方根是
的立方根是
正数
负数
零
观察归纳
的立方根是负数
正数
负数
零
观察归纳
立方根的性质
正数的立方根是正数;
负数的立方根是负数;
零的立方根是零.
学习新知
例2 求下列各式的值:
(1) ; (2) .
学以致用
3
3
例2 求下列各式的值:
(1) ;
学以致用
3
因为0.13=0.001,
解: 表示0.001的立方根,
3
所以 .
3
例2 求下列各式的值:
(2)
学以致用
解: 表示-8的立方根,
3
因为 ,
所以 .
3
3
.
知识梳理
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
定义
表示法
性质
平方根
立方根
知识梳理
对比定义
若x2=a,那么 x 叫做 a 的平方根.
若x3=a,那么 x 叫做 a 的立方根.
平方根:
立方根:
知识梳理
(a≥0).
(a为任意数).
对比表示法
平方根:
立方根:
知识梳理
平方根:
立方根:
对比性质
正数有两个平方根,互为相反数
正数有一个立方根,仍为正数
知识梳理
平方根:
立方根:
对比性质
负数没有平方根
负数有一个立方根,是个负数
知识梳理
对比性质
零的平方根是零
零的立方根是零
平方根:
立方根:
2
-2
4
-4
0.5
-0.5
=-
课堂练习
(1) , ;
(2) , ;
(3) , .
你发现了什么规律?
用式子表示出来: .
3
3
3
3
3
3
3
3
填空:
课堂练习
=-
3
3
观察 发现 归纳
例如:
得到:
1.立方根的概念和开立方运算:
求一个数的立方根的运算叫做开立方.
一般地,如果一个数x 的立方等于a,那么这个数x 就叫做a 的立方根.a 的立方根记作:
3
课堂小结
2.如何求一个数的立方根?
立方运算
开立方运算
互为
逆运算
课堂小结
3.立方根的性质:
正数的立方根是正数;
零的立方根是零;
负数的立方根是负数.
课堂小结
平方根
立方根
类比
4.
课堂小结
课后练习
1.求下列各数的立方根:
(1)-1000; (2)0.512.
2.求下列各式的值:
(1) ; (2) ;(3) ; (4) .
3
3
3
3
祝同学们学习进步!
初二年级 数学
问题引入
为了建造一个容积为343立方米,形状为正方体的蓄水池,它的棱长应取多少米?
棱长3=体积
343
?3=
问题引入
为了建造一个容积为343立方米,形状为正方体的蓄水池,它的棱长应取多少米?
问题引入
x
x3=343
为了建造一个容积为343立方米,形状为正方体的蓄水池,它的棱长应取多少米?
问题引入
x3=343
x2=343
x叫343的平方根
x叫343的立方根
平方根的定义
a 的平方根用符号“ ”表示.
如果 x?=a ,那么 x 叫做 a 的平方根.
一般地,如果一个数x的平方等于a ,那么
这个数x就叫做 a 的平方根.
回顾旧知
立方根的定义
一般地,如果一个数x的立方等于a ,那么
这个数x就叫做 a 的立方根.
学习新知
如果 x3=a ,那么 x 叫做a 的立方根.
因为 ,
所以 是 的立方根.
“a 的立方根” 记作:
读作:“三次根号a”
立方根的表示法
3
例如:“8的立方根” 记作:“ ”
3
学习新知
注意:根指数3不能省略.
被开方数
根指数
3
学习新知
9
已知
一个数
±3
求
这个数的平方根
开平方
运算
求
这个数
的平方
3
9
平方
运算
已知
一个数
回顾旧知
已知
一个数
求
这个数的立方根
开立方
运算
求
这个数
的立方
立方
运算
已知
一个数
回顾旧知
2
8
8
2
?
求一个数的立方根的运算叫做开立方.
开立方运算的结果是立方根.
开立方运算 立方运算
互为
逆运算
学习新知
例1 求下列各数的立方根:
(1)27; (2) ;(3) ;(4)-0.001.
学以致用
例1 求下列各数的立方根:
(1)27;
解:
3=27,
( )
因为
所以 ,
3
27的立方根是
3
?
分析:
即
.
3
学以致用
例1 求下列各数的立方根:
(2) ;
( )
因为 ,
解:
的立方根是
所以 ,
,
即
.
3
学以致用
例1 求下列各数的立方根:
(3) ;
解:
( )
3= ,
所以 ,
的立方根是
因为
.
即
3
学以致用
例1 求下列各数的立方根:
(4) .
解:
3=-0.001,
( )
所以
-0.001的立方根是
-0.1,
-0.1
因为
.
即
3
学以致用
求一个数的立方根的方法
立方运算
开立方运算
互为
逆运算
归纳小结
求一个数的立方根的方法
归纳小结
正数有两个平方根,它们互为相反数;
负数没有平方根.
零的平方根是零;
平方根的性质
回顾旧知
1.一个正数有两个平方根,那么一个正数有几个
立方根?
想一想
2.负数没有平方根,那么负数有立方根吗?
回顾旧知
有一个
是个正数
的立方根是
8 的立方根是
的立方根是
正数
负数
零
观察归纳
的立方根是正数
正数
负数
零
观察归纳
0
正数
负数
零
观察归纳
的立方根是零
正数
负数
零
观察归纳
有一个
是个负数
的立方根是
-8 的立方根是
的立方根是
正数
负数
零
观察归纳
的立方根是负数
正数
负数
零
观察归纳
立方根的性质
正数的立方根是正数;
负数的立方根是负数;
零的立方根是零.
学习新知
例2 求下列各式的值:
(1) ; (2) .
学以致用
3
3
例2 求下列各式的值:
(1) ;
学以致用
3
因为0.13=0.001,
解: 表示0.001的立方根,
3
所以 .
3
例2 求下列各式的值:
(2)
学以致用
解: 表示-8的立方根,
3
因为 ,
所以 .
3
3
.
知识梳理
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
定义
表示法
性质
平方根
立方根
知识梳理
对比定义
若x2=a,那么 x 叫做 a 的平方根.
若x3=a,那么 x 叫做 a 的立方根.
平方根:
立方根:
知识梳理
(a≥0).
(a为任意数).
对比表示法
平方根:
立方根:
知识梳理
平方根:
立方根:
对比性质
正数有两个平方根,互为相反数
正数有一个立方根,仍为正数
知识梳理
平方根:
立方根:
对比性质
负数没有平方根
负数有一个立方根,是个负数
知识梳理
对比性质
零的平方根是零
零的立方根是零
平方根:
立方根:
2
-2
4
-4
0.5
-0.5
=-
课堂练习
(1) , ;
(2) , ;
(3) , .
你发现了什么规律?
用式子表示出来: .
3
3
3
3
3
3
3
3
填空:
课堂练习
=-
3
3
观察 发现 归纳
例如:
得到:
1.立方根的概念和开立方运算:
求一个数的立方根的运算叫做开立方.
一般地,如果一个数x 的立方等于a,那么这个数x 就叫做a 的立方根.a 的立方根记作:
3
课堂小结
2.如何求一个数的立方根?
立方运算
开立方运算
互为
逆运算
课堂小结
3.立方根的性质:
正数的立方根是正数;
零的立方根是零;
负数的立方根是负数.
课堂小结
平方根
立方根
类比
4.
课堂小结
课后练习
1.求下列各数的立方根:
(1)-1000; (2)0.512.
2.求下列各式的值:
(1) ; (2) ;(3) ; (4) .
3
3
3
3
祝同学们学习进步!
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
