京改版八年级上册12.2三角形的性质(1)课件(共61张ppt)
文档属性
| 名称 | 京改版八年级上册12.2三角形的性质(1)课件(共61张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 20:37:08 | ||
图片预览









文档简介
三角形的性质(1)
初二年级 数学
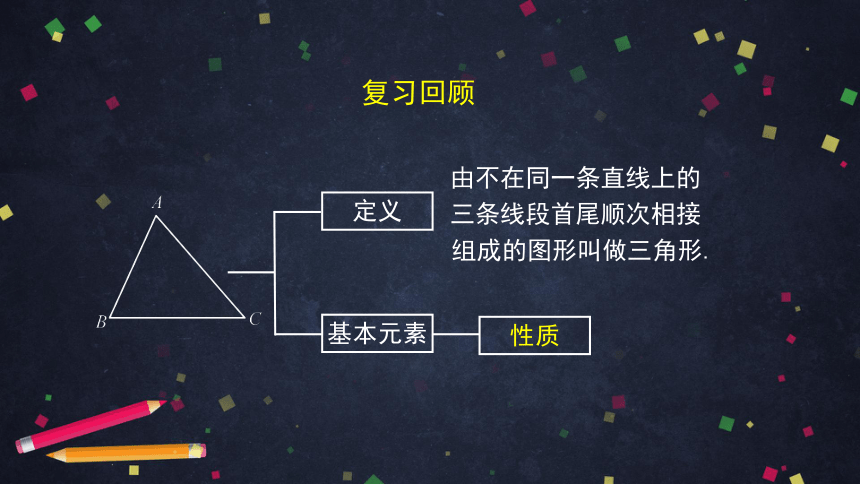
复习回顾
基本元素
由不在同一条直线上的
三条线段首尾顺次相接
组成的图形叫做三角形.
定义
性质
探究新知
北京首个全向十字路口,
设于石景山鲁谷西街与郑
达路交叉处.
探究新知
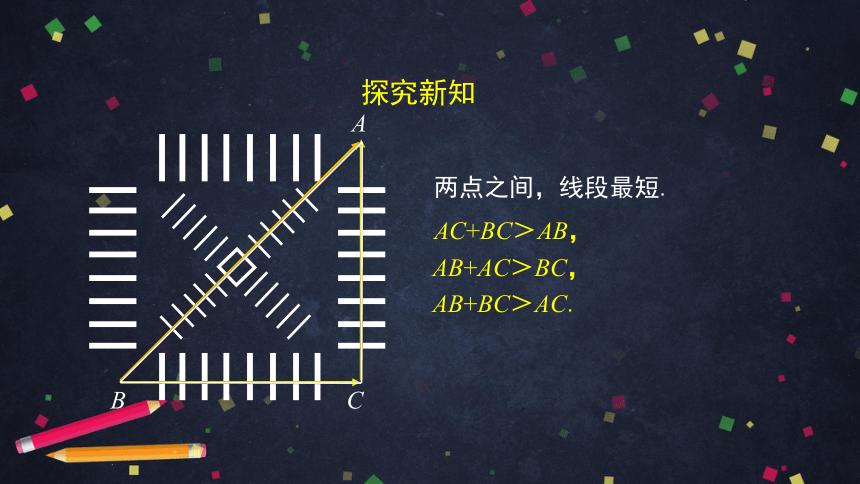
两点之间,线段最短.
AB+AC>BC,
AB+BC>AC.
AC+BC>AB,
A
B
C
1.三角形两边之和大于第三边.
探究新知
三角形边的性质
1.三角形两边之和大于第三边.
符号语言 ∵△ABC,
∴AB+AC>BC,
AB+BC>AC,
BC+AC>AB.
探究新知
三角形边的性质
1.三角形两边之和大于第三边.
符号语言 ∵△ABC,
∴AB+AC>BC,
AB+BC>AC,
BC+AC>AB.
特点
探究新知
三角形边的性质
?
三角形三边的数量关系.
三角形三边不相等的数量关系.
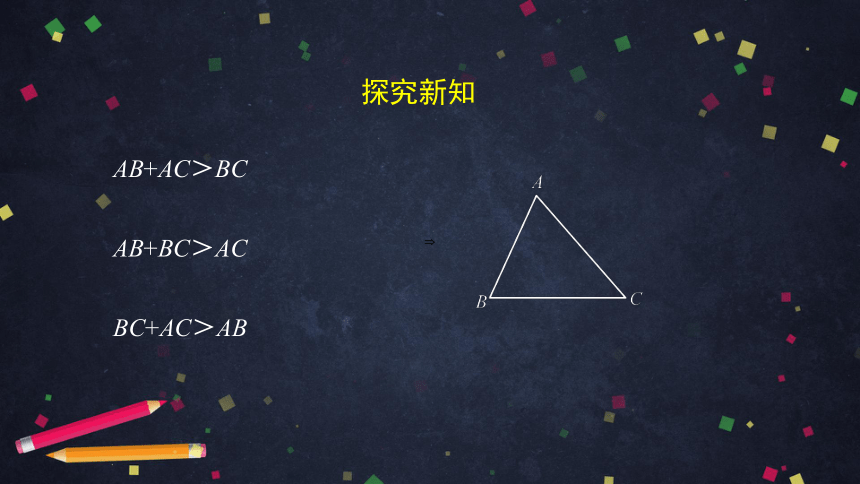
AB+AC>BC
AB+BC>AC
BC+AC>AB
探究新知
AB+AC>BC AB>BC-AC
AC>BC-AB
AB+BC>AC
BC+AC>AB
探究新知
依据:不等式的基本性质1
AB+AC>BC AB>BC-AC
AC>BC-AB
AB+BC>AC BC>AC-AB
AB>AC-BC
BC+AC>AB AC>AB-BC
BC>AB-AC
探究新知
依据:不等式的基本性质1
2.三角形两边之差小于第三边.
探究新知
三角形边的性质
2.三角形两边之差小于第三边.
符号语言 ∵△ABC,
∴BC-AC<AB,
AC-AB<BC,
BC-AB<AC.
探究新知
三角形边的性质
探究新知
概括 ?
1.三角形两边之和大于第三边.
2.三角形两边之差小于第三边.
三角形边的性质
探究新知
概括:
其余两边之差<某一边<其余两边之和
1.三角形两边之和大于第三边.
2.三角形两边之差小于第三边.
三角形边的性质
探究新知
BC=AB-AC
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
在△ABC中,BC与AB,AC之间的关系?
BC=AB+AC
探究新知
BC=AB-AC
BC=AB+AC
AB-AC<BC<AB+AC
其余两边之差<某一边<其余两边之和
例 长度为下列各组数值的三条线段能否首尾顺次
相接组成一个三角形?
例题讲解
(1)6,10,4
(2)5,4,8
(3)5,10,4
(1)6,10,4 (2)5,4,8 (3)5,10,4
分析:要构成三角形,需满足
AB+AC>BC,
AB+BC>AC,
BC+AC>AB.
例题讲解
(1)6,10,4 (2)5,4,8 (3)5,10,4
解:
例题讲解
6+10>4,
4+10>6,
6+4=10,
不可以
5+4>8,
4+8>5,
5+8>4,
可以
5+10>4,
4+10>5,
5+4<10,
不可以
有没有必要再验证两边之差小于第三边?
(1)6,10,4 (2)5,4,8 (3)5,10,4
分析:
例题讲解
没有必要再验证两边之差小于第三边
三角形两边之和大于第三边
三角形两边之差小于第三边
本质相同
(1)6,10,4 (2)5,4,8 (3)5,10,4
解:
例题讲解
6+10>4,
4+10>6,
6+4=10,
不可以
5+4>8,
4+8>5,
5+8>4,
可以
5+10>4,
4+10>5,
5+4<10,
不可以
判断三条线段能否组成三角形有没有更
简便的方法?
(1)6,10,4 (2)5,4,8 (3)5,10,4
解:
例题讲解
6+10>4,
4+10>6,
6+4=10,
不可以
5+4>8,
4+8>5,
5+8>4,
可以
5+10>4,
4+10>5,
5+4<10,
不可以
判断三条线段能否组成三角形有没有更
简便的方法?
(1)6,10,4 (2)5,4,8 (3)5,10,4
解:
例题讲解
6+10>4,
4+10>6,
6+4=10,
不可以
5+4>8,
4+8>5,
5+8>4,
可以
5+10>4,
4+10>5,
5+4<10,
不可以
判断三条线段能否组成三角形有没有更
简便的方法?
(1)6,10,4 (2)5,4,8 (3)5,10,4
解:
例题讲解
6+10>4,
4+10>6,
6+4=10,
不可以
5+4>8,
4+8>5,
5+8>4,
可以
5+10>4,
4+10>5,
5+4<10,
不可以
判断三条线段能否组成三角形有没有更
简便的方法?
(1)6,10,4 (2)5,4,8 (3)5,10,4
解:
例题讲解
6+10>4,
4+10>6,
6+4=10,
不可以
5+4>8,
4+8>5,
5+8>4,
可以
5+10>4,
4+10>5,
5+4<10,
不可以
判断三条线段能否组成三角形有没有更
简便的方法?
例题总结
选取两条较短的线段求和
和与最长的线段比较
可以组成三角形
线段和>最长线段
不可以组成三角形
线段和≤最长线段
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
例题讲解
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
例题讲解
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
例题讲解
腰+腰+底=12
例题讲解
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
分析:周长=12
腰+腰+底=12
例题讲解
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
分析:周长=12
例题讲解
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
分析:周长=12
腰+腰+底=12
3?
3?
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
例题讲解
分类讨论
情况1 3cm长的边为底,
情况2 3cm长的边为腰.
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
解:如果3cm长的边为底,设腰长为xcm.
例题讲解
3,4.5,4.5?
x+x+3=12,解得x=4.5.
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
解:如果3cm长的边为底,设腰长为xcm.
例题讲解
x+x+3=12,解得x=4.5.
∵ 3+4.5>4.5
∴ 3,4.5,4.5可以构成三角形.
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
解:如果3cm长的边为腰,设底边长为ycm.
例题讲解
3,3,6?
y+3+3=12,解得y=6.
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
解:如果3cm长的边为腰,设底边长为ycm.
例题讲解
∵ 3+3=6
∴ 3,3,6不可以构成三角形.
答:另外两边的长是4.5cm,4.5cm.
y+3+3=12,解得y=6.
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
例题小结
3cm长的边为底.
x+x+3=12,x=4.5
∵3+4.5>4.5
∴可以构成三角形.
3cm长的边为腰.
3+3+y=12,y=6
∵3+3=6
∴不可以构成三角形.
圈画关键词
画图分析
分类讨论
方程思想
验证
例题讲解
例 已知在△ABC中,
(1)a=3,b=4,求c的取值范围.
例 已知在△ABC中,
例题讲解
分析:三角形某一边的长度大于其余两边之差,
小于其余两边之和.
(1)a=3,b=4,求c的取值范围.
例 已知在△ABC中,
例题讲解
解:
∵b-a<c<b+a,
∴4-3<c<4+3.
即1<c<7.
(1)a=3,b=4,求c的取值范围.
例 已知在△ABC中,
例题讲解
解:
(1)a=3,b=4,求c的取值范围.
∵a-b<c<a+b,
∴3-4<c<3+4.
即-1<c<7.
是否有必要?
∵b-a<c<b+a,
∴4-3<c<4+3.
即1<c<7.
例 已知在△ABC中,
例题讲解
解:
(1)a=3,b=4,求c的取值范围.
∵a-b<c<a+b,
∴3-4<c<3+4.
即-1<c<7.
∵b-a<c<b+a,
∴4-3<c<4+3.
即1<c<7.
大于0
两边之差小于第三边
例 已知在△ABC中,
例题讲解
解:
(1)a=3,b=4,求c的取值范围.
∵a-b<c<a+b,
∴3-4<c<3+4.
即-1<c<7.
∵b-a<c<b+a,
∴4-3<c<4+3.
即1<c<7.
大于0
两边之差小于第三边
长边-短边
例 已知在△ABC中,
例题讲解
(2)a=3,b=4,如果第三边的长是一个偶数,
求第三边的长.
例 已知在△ABC中,
例题讲解
(2)a=3,b=4,如果第三边的长是一个偶数,
求第三边的长.
例 已知在△ABC中,
例题讲解
(2)a=3,b=4,如果第三边的长是一个偶数,
求第三边的长.
∵1<c<7且c为偶数,
∴c=2,4,6.
解:
课堂小结
本节课你有什么收获和体会?
课堂小结
其余两边之差<某一边<其余两边之和
1.两点之间线段最短(基本事实)
三角形边的性质1
三角形边的性质2
不等式的
基本性质
2.等腰三角形
课堂小结
方程思想
分类讨论
2.等腰三角形
3.阅读题目时,圈画关键词,有助于题目的分析与理解.
课堂小结
方程思想
分类讨论
1.三角形中,其中两条边长分别是3cm和4cm,
求第三条边的长度的取值范围.
2.有长分别为2cm,3cm,4cm,5cm的四根木棍,
用其中的三根首尾相接组成三角形,共有多少
种组成方法?
课后作业
同学们再见
初二年级 数学
复习回顾
基本元素
由不在同一条直线上的
三条线段首尾顺次相接
组成的图形叫做三角形.
定义
性质
探究新知
北京首个全向十字路口,
设于石景山鲁谷西街与郑
达路交叉处.
探究新知
两点之间,线段最短.
AB+AC>BC,
AB+BC>AC.
AC+BC>AB,
A
B
C
1.三角形两边之和大于第三边.
探究新知
三角形边的性质
1.三角形两边之和大于第三边.
符号语言 ∵△ABC,
∴AB+AC>BC,
AB+BC>AC,
BC+AC>AB.
探究新知
三角形边的性质
1.三角形两边之和大于第三边.
符号语言 ∵△ABC,
∴AB+AC>BC,
AB+BC>AC,
BC+AC>AB.
特点
探究新知
三角形边的性质
?
三角形三边的数量关系.
三角形三边不相等的数量关系.
AB+AC>BC
AB+BC>AC
BC+AC>AB
探究新知
AB+AC>BC AB>BC-AC
AC>BC-AB
AB+BC>AC
BC+AC>AB
探究新知
依据:不等式的基本性质1
AB+AC>BC AB>BC-AC
AC>BC-AB
AB+BC>AC BC>AC-AB
AB>AC-BC
BC+AC>AB AC>AB-BC
BC>AB-AC
探究新知
依据:不等式的基本性质1
2.三角形两边之差小于第三边.
探究新知
三角形边的性质
2.三角形两边之差小于第三边.
符号语言 ∵△ABC,
∴BC-AC<AB,
AC-AB<BC,
BC-AB<AC.
探究新知
三角形边的性质
探究新知
概括 ?
1.三角形两边之和大于第三边.
2.三角形两边之差小于第三边.
三角形边的性质
探究新知
概括:
其余两边之差<某一边<其余两边之和
1.三角形两边之和大于第三边.
2.三角形两边之差小于第三边.
三角形边的性质
探究新知
BC=AB-AC
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
在△ABC中,BC与AB,AC之间的关系?
BC=AB+AC
探究新知
BC=AB-AC
BC=AB+AC
AB-AC<BC<AB+AC
其余两边之差<某一边<其余两边之和
例 长度为下列各组数值的三条线段能否首尾顺次
相接组成一个三角形?
例题讲解
(1)6,10,4
(2)5,4,8
(3)5,10,4
(1)6,10,4 (2)5,4,8 (3)5,10,4
分析:要构成三角形,需满足
AB+AC>BC,
AB+BC>AC,
BC+AC>AB.
例题讲解
(1)6,10,4 (2)5,4,8 (3)5,10,4
解:
例题讲解
6+10>4,
4+10>6,
6+4=10,
不可以
5+4>8,
4+8>5,
5+8>4,
可以
5+10>4,
4+10>5,
5+4<10,
不可以
有没有必要再验证两边之差小于第三边?
(1)6,10,4 (2)5,4,8 (3)5,10,4
分析:
例题讲解
没有必要再验证两边之差小于第三边
三角形两边之和大于第三边
三角形两边之差小于第三边
本质相同
(1)6,10,4 (2)5,4,8 (3)5,10,4
解:
例题讲解
6+10>4,
4+10>6,
6+4=10,
不可以
5+4>8,
4+8>5,
5+8>4,
可以
5+10>4,
4+10>5,
5+4<10,
不可以
判断三条线段能否组成三角形有没有更
简便的方法?
(1)6,10,4 (2)5,4,8 (3)5,10,4
解:
例题讲解
6+10>4,
4+10>6,
6+4=10,
不可以
5+4>8,
4+8>5,
5+8>4,
可以
5+10>4,
4+10>5,
5+4<10,
不可以
判断三条线段能否组成三角形有没有更
简便的方法?
(1)6,10,4 (2)5,4,8 (3)5,10,4
解:
例题讲解
6+10>4,
4+10>6,
6+4=10,
不可以
5+4>8,
4+8>5,
5+8>4,
可以
5+10>4,
4+10>5,
5+4<10,
不可以
判断三条线段能否组成三角形有没有更
简便的方法?
(1)6,10,4 (2)5,4,8 (3)5,10,4
解:
例题讲解
6+10>4,
4+10>6,
6+4=10,
不可以
5+4>8,
4+8>5,
5+8>4,
可以
5+10>4,
4+10>5,
5+4<10,
不可以
判断三条线段能否组成三角形有没有更
简便的方法?
(1)6,10,4 (2)5,4,8 (3)5,10,4
解:
例题讲解
6+10>4,
4+10>6,
6+4=10,
不可以
5+4>8,
4+8>5,
5+8>4,
可以
5+10>4,
4+10>5,
5+4<10,
不可以
判断三条线段能否组成三角形有没有更
简便的方法?
例题总结
选取两条较短的线段求和
和与最长的线段比较
可以组成三角形
线段和>最长线段
不可以组成三角形
线段和≤最长线段
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
例题讲解
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
例题讲解
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
例题讲解
腰+腰+底=12
例题讲解
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
分析:周长=12
腰+腰+底=12
例题讲解
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
分析:周长=12
例题讲解
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
分析:周长=12
腰+腰+底=12
3?
3?
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
例题讲解
分类讨论
情况1 3cm长的边为底,
情况2 3cm长的边为腰.
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
解:如果3cm长的边为底,设腰长为xcm.
例题讲解
3,4.5,4.5?
x+x+3=12,解得x=4.5.
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
解:如果3cm长的边为底,设腰长为xcm.
例题讲解
x+x+3=12,解得x=4.5.
∵ 3+4.5>4.5
∴ 3,4.5,4.5可以构成三角形.
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
解:如果3cm长的边为腰,设底边长为ycm.
例题讲解
3,3,6?
y+3+3=12,解得y=6.
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
解:如果3cm长的边为腰,设底边长为ycm.
例题讲解
∵ 3+3=6
∴ 3,3,6不可以构成三角形.
答:另外两边的长是4.5cm,4.5cm.
y+3+3=12,解得y=6.
例 已知等腰三角形的周长为12cm,其中一边的长
为3cm,求另外两边的长.
例题小结
3cm长的边为底.
x+x+3=12,x=4.5
∵3+4.5>4.5
∴可以构成三角形.
3cm长的边为腰.
3+3+y=12,y=6
∵3+3=6
∴不可以构成三角形.
圈画关键词
画图分析
分类讨论
方程思想
验证
例题讲解
例 已知在△ABC中,
(1)a=3,b=4,求c的取值范围.
例 已知在△ABC中,
例题讲解
分析:三角形某一边的长度大于其余两边之差,
小于其余两边之和.
(1)a=3,b=4,求c的取值范围.
例 已知在△ABC中,
例题讲解
解:
∵b-a<c<b+a,
∴4-3<c<4+3.
即1<c<7.
(1)a=3,b=4,求c的取值范围.
例 已知在△ABC中,
例题讲解
解:
(1)a=3,b=4,求c的取值范围.
∵a-b<c<a+b,
∴3-4<c<3+4.
即-1<c<7.
是否有必要?
∵b-a<c<b+a,
∴4-3<c<4+3.
即1<c<7.
例 已知在△ABC中,
例题讲解
解:
(1)a=3,b=4,求c的取值范围.
∵a-b<c<a+b,
∴3-4<c<3+4.
即-1<c<7.
∵b-a<c<b+a,
∴4-3<c<4+3.
即1<c<7.
大于0
两边之差小于第三边
例 已知在△ABC中,
例题讲解
解:
(1)a=3,b=4,求c的取值范围.
∵a-b<c<a+b,
∴3-4<c<3+4.
即-1<c<7.
∵b-a<c<b+a,
∴4-3<c<4+3.
即1<c<7.
大于0
两边之差小于第三边
长边-短边
例 已知在△ABC中,
例题讲解
(2)a=3,b=4,如果第三边的长是一个偶数,
求第三边的长.
例 已知在△ABC中,
例题讲解
(2)a=3,b=4,如果第三边的长是一个偶数,
求第三边的长.
例 已知在△ABC中,
例题讲解
(2)a=3,b=4,如果第三边的长是一个偶数,
求第三边的长.
∵1<c<7且c为偶数,
∴c=2,4,6.
解:
课堂小结
本节课你有什么收获和体会?
课堂小结
其余两边之差<某一边<其余两边之和
1.两点之间线段最短(基本事实)
三角形边的性质1
三角形边的性质2
不等式的
基本性质
2.等腰三角形
课堂小结
方程思想
分类讨论
2.等腰三角形
3.阅读题目时,圈画关键词,有助于题目的分析与理解.
课堂小结
方程思想
分类讨论
1.三角形中,其中两条边长分别是3cm和4cm,
求第三条边的长度的取值范围.
2.有长分别为2cm,3cm,4cm,5cm的四根木棍,
用其中的三根首尾相接组成三角形,共有多少
种组成方法?
课后作业
同学们再见
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
