京改版八年级上册12.2三角形的性质(2)课件(共46张ppt)
文档属性
| 名称 | 京改版八年级上册12.2三角形的性质(2)课件(共46张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 20:38:05 | ||
图片预览






文档简介
三角形的性质(2)
初二年级 数学
复习回顾
三角形的性质
边的性质
角的性质
三角形的两边之和大于第三边,
三角形的两边之差小于第三边.
复习回顾
外角
内角
三角形的性质
边的性质
角的性质
某博物馆墙面采用玻璃材质,
其中一块三角形玻璃不小心被
打碎,已知没有被打碎的两个
角分别是 和 ,则被打碎
的角是多少度?
情景引入
答: ,因为三角形三个内角的和为 .
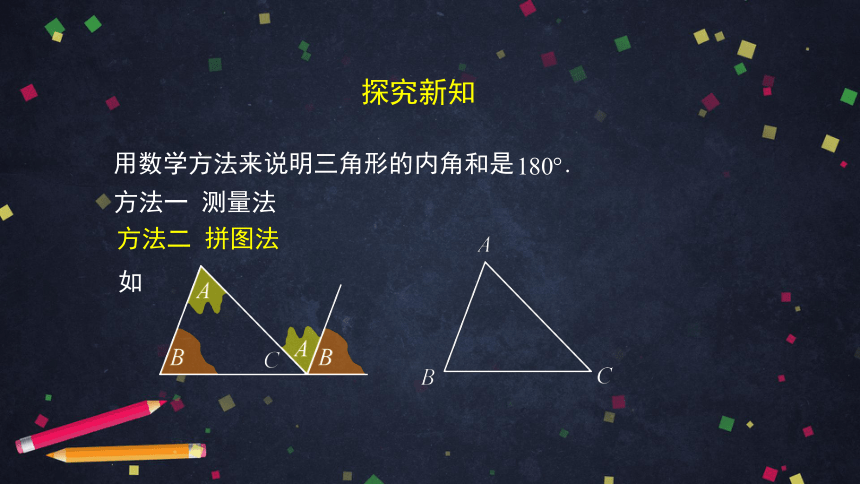
用数学方法来说明三角形的内角和是 .
探究新知
方法一 测量法
用数学方法来说明三角形的内角和是 .
探究新知
方法一 测量法
方法二 拼图法
如
命题: 三角形三个内角的和等于 .
探究新知
探究新知
已知: △ ABC .
求证: .
命题: 三角形三个内角的和等于 .
探究新知
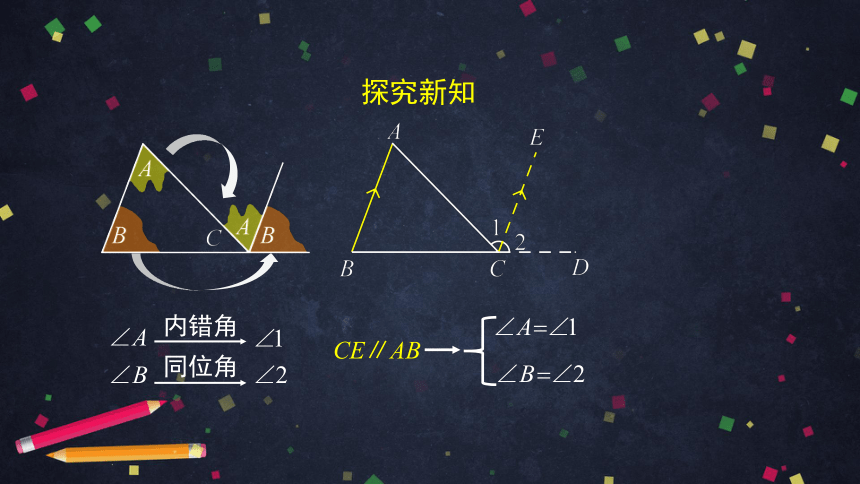
内错角
同位角
CE∥AB
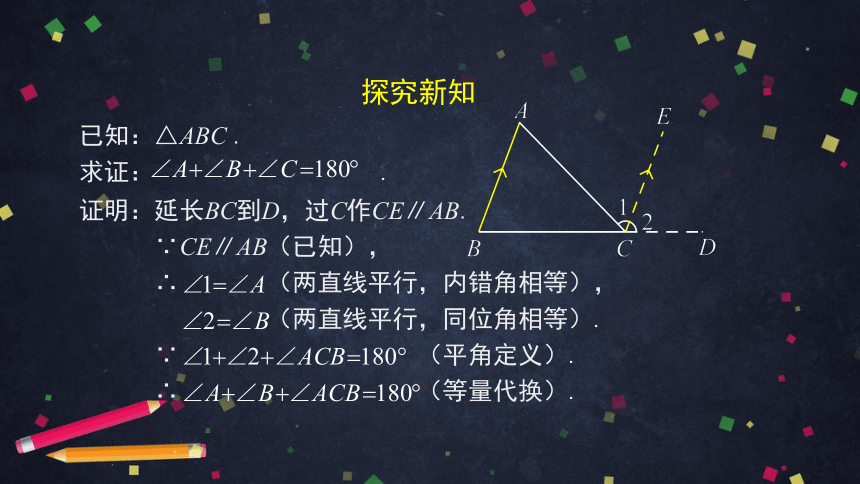
已知:△ABC . 求证: .
证明:延长BC到D,过C作CE∥AB.
∵CE∥AB(已知),
∴ (两直线平行,内错角相等),
(两直线平行,同位角相等).
∵ (平角定义).
∴ (等量代换).
探究新知
探究新知
EF∥BC
分析:
已知:△ABC . 求证: .
∠A+∠B+∠C=180°
∠1=∠B
∠3=∠C
∠1+∠2+∠3=180°
∠B+∠BAC+∠C=180°
∠A +∠B +∠C
平行线转移角
∠1+∠2+∠3
(分散的角)
(共顶点的角)
已知:△ABC . 求证: .
证明:过A作EF∥BC.
∵EF∥BC (已知),
∴∠1=∠B,∠3=∠C.
(两直线平行,内错角相等)
∵∠1+∠2+∠3=180°(平角定义),
∴∠B+∠2+∠C=180°(等量代换).
探究新知
∠A+∠B+∠C=180°
探究新知
平角等于
两直线平行,同旁内角互补
已知:△ABC . 求证: .
∠A+∠B+∠C=180°
探究新知
CE∥AB
已知:△ABC . 求证: .
分析:
∠A+∠B+∠C=180°
已知:△ABC . 求证: .
证明:过C作CE∥AB.
∵ CE∥AB (已知),
∴∠1=∠A(两直线平行,内错角相等).
∠B+∠ACB+∠1=180°(两直线平行,同旁内角互补).
∴∠B+∠ACB+∠A=180°(等量代换).
探究新知
∠A+∠B+∠C=180°
探究新知
在顶点C
其他位置?
探究新知
在边上任取一点D
分析:
过D作AC的平行线
∠A ∠1
∠C ∠2
同位角
同位角
探究新知
过D作AC的平行线
过D作AB的平行线
在边上任取一点D
分析:
∠A ∠1
∠C ∠2
同位角
同位角
探究新知
过D作AC的平行线
过D作AB的平行线
在边上任取一点D
分析:
∠A ∠1 ∠4
∠C ∠2
∠B ∠3
同位角
同位角
内错角
同位角
∠A +∠B +∠C
∠4 +∠3 +∠2
探究新知
平行线转移角
探究新知
平行线转移角
在三角形内
在三角形外
探究新知
平行线转移角
在顶点处
在边上
在三角形内
在三角形外
三角形内角和定理:三角形三个内角的和等于 .
探究新知
符号语言:
在△ABC中, ∠A+∠B+∠C= .
①通过平行线转移角
探究新知
在△ABC中, ∠A+∠B+∠C= .
符号语言:
三角形内角和定理:三角形三个内角的和等于 .
①通过平行线转移角
②三角形三个内角的等量关系
探究新知
符号语言:
在△ABC中, ∠A+∠B+∠C= .
三角形内角和定理:三角形三个内角的和等于 .
五边形
六边形
n边形
……
四边形
探究新知
…
分析:
∠1+∠2+∠B=180°
∠3+∠4+∠D=180°
(∠1+∠4)+∠B+(∠2+∠3)+∠D=360°
∠BAD+∠B+∠BCD+∠D=360°
探究新知
↓
分析:
↓
探究新知
↓
?
分析:
↓
探究新知
↓
分割法
思考:多边形转化为
三角形的其他方法?
探究新知
五边形
六边形
n边形
……
四边形
…
探究新知
五边形
六边形
n边形
……
四边形
…
探究新知
五边形
六边形
n边形
……
四边形
…
探究新知
五边形
六边形
n边形
……
四边形
n边形内角和:
…
例题讲解
例 如图,在△ABC中,∠A= ,
∠B=∠C.求∠B,∠C的度数.
解:设∠B为 ,
∵∠B=∠C,
∴∠C也为 .
∵∠A+∠B+∠C= (三角形内角和定理),
∴100+x+ x=180,2x=80,得x=40.
即∠B= ,∠C= .
例 如图,在△ABC中,∠A= ,
∠B=∠C.求∠B,∠C的度数.
例 计算下列三角形中标有x的角的度数.
例题讲解
(1) (2) (3)
例 计算下列三角形中标有x的角的度数.
例题讲解
(1) (2) (3)
例 计算下列三角形中标有x的角的度数.
例题讲解
(1) (2) (3)
例 计算下列三角形中标有x的角的度数.
例题讲解
(1) (2) (3)
+ + =
x
x
x
例题讲解
例 一副三角板,如图所示叠放在一起,求
图中重合的∠ 的度数.
例题讲解
解:∵在△AEC中,
∠AEC+∠ +∠C= .
∴∠ = = .
例 一副三角板,如图所示叠放在一起,求
图中重合的∠ 的度数.
课堂总结
本节课你有什么收获和体会?
课堂总结
1.三角形三个内角的和等于180°.
2.n边形(n≥3)的内角和等于( -2)×180°.
作平行线 角的位置
多边形 三角形
转移
转化
分割法
课后作业
2.已知:如图,△ABC中,D是CA
延长线上一点,AE是∠DAB的
平分线,∠B= ,∠C= .
求∠DAE的度数.
1.三角形三个内角的度数的比为1∶2∶3.
求这三个内角的度数.
同学们再见!
初二年级 数学
复习回顾
三角形的性质
边的性质
角的性质
三角形的两边之和大于第三边,
三角形的两边之差小于第三边.
复习回顾
外角
内角
三角形的性质
边的性质
角的性质
某博物馆墙面采用玻璃材质,
其中一块三角形玻璃不小心被
打碎,已知没有被打碎的两个
角分别是 和 ,则被打碎
的角是多少度?
情景引入
答: ,因为三角形三个内角的和为 .
用数学方法来说明三角形的内角和是 .
探究新知
方法一 测量法
用数学方法来说明三角形的内角和是 .
探究新知
方法一 测量法
方法二 拼图法
如
命题: 三角形三个内角的和等于 .
探究新知
探究新知
已知: △ ABC .
求证: .
命题: 三角形三个内角的和等于 .
探究新知
内错角
同位角
CE∥AB
已知:△ABC . 求证: .
证明:延长BC到D,过C作CE∥AB.
∵CE∥AB(已知),
∴ (两直线平行,内错角相等),
(两直线平行,同位角相等).
∵ (平角定义).
∴ (等量代换).
探究新知
探究新知
EF∥BC
分析:
已知:△ABC . 求证: .
∠A+∠B+∠C=180°
∠1=∠B
∠3=∠C
∠1+∠2+∠3=180°
∠B+∠BAC+∠C=180°
∠A +∠B +∠C
平行线转移角
∠1+∠2+∠3
(分散的角)
(共顶点的角)
已知:△ABC . 求证: .
证明:过A作EF∥BC.
∵EF∥BC (已知),
∴∠1=∠B,∠3=∠C.
(两直线平行,内错角相等)
∵∠1+∠2+∠3=180°(平角定义),
∴∠B+∠2+∠C=180°(等量代换).
探究新知
∠A+∠B+∠C=180°
探究新知
平角等于
两直线平行,同旁内角互补
已知:△ABC . 求证: .
∠A+∠B+∠C=180°
探究新知
CE∥AB
已知:△ABC . 求证: .
分析:
∠A+∠B+∠C=180°
已知:△ABC . 求证: .
证明:过C作CE∥AB.
∵ CE∥AB (已知),
∴∠1=∠A(两直线平行,内错角相等).
∠B+∠ACB+∠1=180°(两直线平行,同旁内角互补).
∴∠B+∠ACB+∠A=180°(等量代换).
探究新知
∠A+∠B+∠C=180°
探究新知
在顶点C
其他位置?
探究新知
在边上任取一点D
分析:
过D作AC的平行线
∠A ∠1
∠C ∠2
同位角
同位角
探究新知
过D作AC的平行线
过D作AB的平行线
在边上任取一点D
分析:
∠A ∠1
∠C ∠2
同位角
同位角
探究新知
过D作AC的平行线
过D作AB的平行线
在边上任取一点D
分析:
∠A ∠1 ∠4
∠C ∠2
∠B ∠3
同位角
同位角
内错角
同位角
∠A +∠B +∠C
∠4 +∠3 +∠2
探究新知
平行线转移角
探究新知
平行线转移角
在三角形内
在三角形外
探究新知
平行线转移角
在顶点处
在边上
在三角形内
在三角形外
三角形内角和定理:三角形三个内角的和等于 .
探究新知
符号语言:
在△ABC中, ∠A+∠B+∠C= .
①通过平行线转移角
探究新知
在△ABC中, ∠A+∠B+∠C= .
符号语言:
三角形内角和定理:三角形三个内角的和等于 .
①通过平行线转移角
②三角形三个内角的等量关系
探究新知
符号语言:
在△ABC中, ∠A+∠B+∠C= .
三角形内角和定理:三角形三个内角的和等于 .
五边形
六边形
n边形
……
四边形
探究新知
…
分析:
∠1+∠2+∠B=180°
∠3+∠4+∠D=180°
(∠1+∠4)+∠B+(∠2+∠3)+∠D=360°
∠BAD+∠B+∠BCD+∠D=360°
探究新知
↓
分析:
↓
探究新知
↓
?
分析:
↓
探究新知
↓
分割法
思考:多边形转化为
三角形的其他方法?
探究新知
五边形
六边形
n边形
……
四边形
…
探究新知
五边形
六边形
n边形
……
四边形
…
探究新知
五边形
六边形
n边形
……
四边形
…
探究新知
五边形
六边形
n边形
……
四边形
n边形内角和:
…
例题讲解
例 如图,在△ABC中,∠A= ,
∠B=∠C.求∠B,∠C的度数.
解:设∠B为 ,
∵∠B=∠C,
∴∠C也为 .
∵∠A+∠B+∠C= (三角形内角和定理),
∴100+x+ x=180,2x=80,得x=40.
即∠B= ,∠C= .
例 如图,在△ABC中,∠A= ,
∠B=∠C.求∠B,∠C的度数.
例 计算下列三角形中标有x的角的度数.
例题讲解
(1) (2) (3)
例 计算下列三角形中标有x的角的度数.
例题讲解
(1) (2) (3)
例 计算下列三角形中标有x的角的度数.
例题讲解
(1) (2) (3)
例 计算下列三角形中标有x的角的度数.
例题讲解
(1) (2) (3)
+ + =
x
x
x
例题讲解
例 一副三角板,如图所示叠放在一起,求
图中重合的∠ 的度数.
例题讲解
解:∵在△AEC中,
∠AEC+∠ +∠C= .
∴∠ = = .
例 一副三角板,如图所示叠放在一起,求
图中重合的∠ 的度数.
课堂总结
本节课你有什么收获和体会?
课堂总结
1.三角形三个内角的和等于180°.
2.n边形(n≥3)的内角和等于( -2)×180°.
作平行线 角的位置
多边形 三角形
转移
转化
分割法
课后作业
2.已知:如图,△ABC中,D是CA
延长线上一点,AE是∠DAB的
平分线,∠B= ,∠C= .
求∠DAE的度数.
1.三角形三个内角的度数的比为1∶2∶3.
求这三个内角的度数.
同学们再见!
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
