京改版八年级上册12.3三角形中的主要线段课件(共49张ppt)
文档属性
| 名称 | 京改版八年级上册12.3三角形中的主要线段课件(共49张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览











文档简介
三角形中的主要线段
初二年级 数学
复习引入
定 义
基本元素
性 质
由不在同一条直线上的
三条线段首尾顺次相接
组成的图形叫做三角形.
顶点、边、角
边的性质
角的性质
动手操作
请你画出一个任意△ABC,找到BC边上的中点,标为点D,
并说明你是如何找到中点的?
探究新知
探究新知
度量法
用刻度尺度量线段BC的长,
找到线段BC的中点D.
探究新知
折叠法
对折,使点B与点C重合,折痕所在直线l
与BC边的交点为BC边的中点D.
探究新知
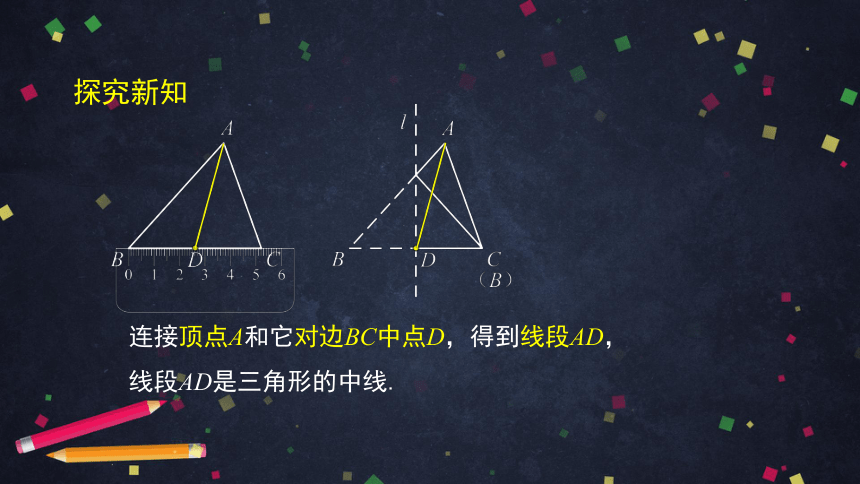
连接顶点A和它对边BC中点D,得到线段AD,
线段AD是三角形的中线.
1.三角形的中线:在三角形中,连接一个顶点和它的对边
中点的线段,叫做这个三角形的中线.
(1)三角形的中线是一条线段.
∵AD是△ABC的中线,
∴BD=CD= BC.
探究新知
请你画出△ABC的其它中线,观察图形,并说明它们之间
存在怎样的位置关系.
(1)三角形的中线是一条线段.
(2)三角形有三条中线,且交于一点,
交点在三角形内部.
探究新知
探究新知
直角三角形和钝角三角形的三条中线是否具备与锐角三角形
三条中线相同的特点呢?
探究新知
锐角三角形、直角三角形和钝角三角形的三条中线
探究新知
1.三角形的中线定义;
2.任意三角形的三条中线交于一点,交点在三角形内部.
动手操作
找一块质地均匀的三角形硬纸板,画出它的三条中线,
用笔尖托住这个交点,观察硬纸板能否保持平衡.
探究新知
探究新知
三角形的三条中线的交点
叫做三角形重心.
动手操作
请你画出一个任意△ABC,及∠BAC的角平分线,
并说明你是如何画角平分线的?
探究新知
探究新知
度量法
用量角器度量∠BAC的大小,
画出∠BAC的角平分线AT.
度量法
用量角器度量∠BAC的大小,
画出∠BAC的角平分线AT,
点T是角平分线与BC边的交点.
探究新知
探究新知
折叠法
折叠,使AB与AC边重叠,折痕所在直线l
是∠BAC的角平分线所在的直线.
探究新知
折叠法
射线AT是∠BAC的角平分线,点T是
∠BAC的角平分线与BC边的交点.
若连接顶点A和交点T,得到线段AT,
这条线段叫做三角形的角平分线.
探究新知
探究新知
1.三角形的角平分线:在三角形中,一个角的平分线与这个角
的对边相交,这个角的顶点与交点之间
的线段,叫做这个三角形的角平分线.
∵AT是△ABC的角平分线,
∴∠BAT=∠CAT= ∠BAC.
请你画出锐角三角形、直角三角形和钝角三角形
的三条角平分线,并观察图形有什么特点?
探究新知
探究新知
1.三角形角平分线定义;
2.三角形的三条角平分线交于一点,交点在三角形内部.
例题讲解
如图,BD是△ABC的角平分线,CE是△ABC的中线,
EF是 的中线;BF是 的角平分线.
△ABF
例题讲解
△BEC
如图,BD是△ABC的角平分线,CE是△ABC的中线,
EF是 的中线;BF是 的角平分线.
△ABF
探究新知
中线
角平分线
?
三角形中的主要线段
探究新知
动手操作
请你画出一个任意△ABC,并过顶点A向它
对边BC所在的直线画垂线段,垂足为H.
探究新知
用三角板的一条直角边贴紧顶点A
的对边BC,另一条直角边过点A,
画出垂线段AH,垂足为H.
探究新知
顶点A与垂足H之间的垂线段AH,
是三角形的高线.
1.三角形的高线:由三角形的一个顶点向它的对边所在的
直线引垂线,顶点和垂足之间的线段叫
做这个三角形的高线,简称三角形的高.
∵AH是△ABC的高,
∴∠AHB=∠AHC=90°.
探究新知
探究新知
已知△ABC,请你画出BC边上的高.
探究新知
已知△ABC,请你画出BC边上的高.
已知△ABC,画AC边上的高.
探究新知
在△ABC中,CE是AB边上的高吗?
探究新知
请你画出锐角三角形、直角三角形和钝角三角形的三条高,
并观察图形有什么特点?
探究新知
探究新知
锐角三角形、直角三角形和钝角三角形的三条高.
探究新知
内部
直角顶点
锐角三角形
直角三角形
外部
钝角三角形
1.三角形的高线定义;
2.任意三角形的三条高所在的直线相交于一点,
锐角三角形的三条高交点在三角形内部,
直角三角形的三条高交点是直角顶点,
钝角三角形的三条高所在直线交点在三角形的外部.
探究新知
如图,AD⊥CD,BE⊥AF于B,CF⊥AF,在△ABC中,
BC边上的高是 ,在△AFC中CF边上的高是 .
例题讲解
例题讲解
如图,AD⊥CD,BE⊥AF,CF⊥AF,在△ABC中,
BC边上的高是 ,在△AFC中CF边上的高是 .
例题讲解
AD
如图,AD⊥CD,BE⊥AF,CF⊥AF,在△ABC中,
BC边上的高是 ,在△AFC中CF边上的高是 .
从复杂图形中分离出目标图形
例题讲解
如图,AD⊥CD,BE⊥AF,CF⊥AF,在△ABC中,
BC边上的高是 ,在△AFC中CF边上的高是 .
AD
例题讲解
AF
AD
如图,AD⊥CD,BE⊥AF,CF⊥AF,在△ABC中,
BC边上的高是 ,在△AFC中CF边上的高是 .
三角形的中线可以得到线段的相等关系,
它还有什么作用?
BD=CD
探究新知
AH=AH
????△????????????=????△????????????
?
探究新知
1.三角形的中线定义;
2.任意三角形的三条中线交于一点,交点在三角形内部;
3.三角形的一条中线将这个三角形分成面积相等的两个三角形.
已知:如图,在△ABC中,点D,E分别为BC,
AD的中点,且 =16,则 = .
例题讲解
CE为△ACD的中线
BE为△ABD的中线
8
AD为△ABC的中线
1.三角形中的主要线段
2.准确作图,有助于对图形准确深入的研究
课堂小结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
中 线
角平分线
高 线
图 形
共 同 点
(1)都是线段,其中一个端点都是三角形的顶点;
(2)三角形的中线,角平分线,高线各有三条,并且它们所在的直线都交于一点.
用途举例
(1)得到相等的线段
(2)构造面积相等的三角形
得到相等的角
(1)得到线段间的垂直关系
(2)进行与面积有关的计算
课后作业
1.如图,已知AD为△ABC的中线,AE为△ABC的高线,且
AB=5cm, AC=3cm.
(1)求△ABD与△ACD的周长之差;
(2)判断△ABD与△ACD的面积关系.
课后作业
2.如图,△ABC中,AD⊥BC,CE⊥AB,BC=6,AD=4,AB=7.
求CE的长.
同学们再见!
初二年级 数学
复习引入
定 义
基本元素
性 质
由不在同一条直线上的
三条线段首尾顺次相接
组成的图形叫做三角形.
顶点、边、角
边的性质
角的性质
动手操作
请你画出一个任意△ABC,找到BC边上的中点,标为点D,
并说明你是如何找到中点的?
探究新知
探究新知
度量法
用刻度尺度量线段BC的长,
找到线段BC的中点D.
探究新知
折叠法
对折,使点B与点C重合,折痕所在直线l
与BC边的交点为BC边的中点D.
探究新知
连接顶点A和它对边BC中点D,得到线段AD,
线段AD是三角形的中线.
1.三角形的中线:在三角形中,连接一个顶点和它的对边
中点的线段,叫做这个三角形的中线.
(1)三角形的中线是一条线段.
∵AD是△ABC的中线,
∴BD=CD= BC.
探究新知
请你画出△ABC的其它中线,观察图形,并说明它们之间
存在怎样的位置关系.
(1)三角形的中线是一条线段.
(2)三角形有三条中线,且交于一点,
交点在三角形内部.
探究新知
探究新知
直角三角形和钝角三角形的三条中线是否具备与锐角三角形
三条中线相同的特点呢?
探究新知
锐角三角形、直角三角形和钝角三角形的三条中线
探究新知
1.三角形的中线定义;
2.任意三角形的三条中线交于一点,交点在三角形内部.
动手操作
找一块质地均匀的三角形硬纸板,画出它的三条中线,
用笔尖托住这个交点,观察硬纸板能否保持平衡.
探究新知
探究新知
三角形的三条中线的交点
叫做三角形重心.
动手操作
请你画出一个任意△ABC,及∠BAC的角平分线,
并说明你是如何画角平分线的?
探究新知
探究新知
度量法
用量角器度量∠BAC的大小,
画出∠BAC的角平分线AT.
度量法
用量角器度量∠BAC的大小,
画出∠BAC的角平分线AT,
点T是角平分线与BC边的交点.
探究新知
探究新知
折叠法
折叠,使AB与AC边重叠,折痕所在直线l
是∠BAC的角平分线所在的直线.
探究新知
折叠法
射线AT是∠BAC的角平分线,点T是
∠BAC的角平分线与BC边的交点.
若连接顶点A和交点T,得到线段AT,
这条线段叫做三角形的角平分线.
探究新知
探究新知
1.三角形的角平分线:在三角形中,一个角的平分线与这个角
的对边相交,这个角的顶点与交点之间
的线段,叫做这个三角形的角平分线.
∵AT是△ABC的角平分线,
∴∠BAT=∠CAT= ∠BAC.
请你画出锐角三角形、直角三角形和钝角三角形
的三条角平分线,并观察图形有什么特点?
探究新知
探究新知
1.三角形角平分线定义;
2.三角形的三条角平分线交于一点,交点在三角形内部.
例题讲解
如图,BD是△ABC的角平分线,CE是△ABC的中线,
EF是 的中线;BF是 的角平分线.
△ABF
例题讲解
△BEC
如图,BD是△ABC的角平分线,CE是△ABC的中线,
EF是 的中线;BF是 的角平分线.
△ABF
探究新知
中线
角平分线
?
三角形中的主要线段
探究新知
动手操作
请你画出一个任意△ABC,并过顶点A向它
对边BC所在的直线画垂线段,垂足为H.
探究新知
用三角板的一条直角边贴紧顶点A
的对边BC,另一条直角边过点A,
画出垂线段AH,垂足为H.
探究新知
顶点A与垂足H之间的垂线段AH,
是三角形的高线.
1.三角形的高线:由三角形的一个顶点向它的对边所在的
直线引垂线,顶点和垂足之间的线段叫
做这个三角形的高线,简称三角形的高.
∵AH是△ABC的高,
∴∠AHB=∠AHC=90°.
探究新知
探究新知
已知△ABC,请你画出BC边上的高.
探究新知
已知△ABC,请你画出BC边上的高.
已知△ABC,画AC边上的高.
探究新知
在△ABC中,CE是AB边上的高吗?
探究新知
请你画出锐角三角形、直角三角形和钝角三角形的三条高,
并观察图形有什么特点?
探究新知
探究新知
锐角三角形、直角三角形和钝角三角形的三条高.
探究新知
内部
直角顶点
锐角三角形
直角三角形
外部
钝角三角形
1.三角形的高线定义;
2.任意三角形的三条高所在的直线相交于一点,
锐角三角形的三条高交点在三角形内部,
直角三角形的三条高交点是直角顶点,
钝角三角形的三条高所在直线交点在三角形的外部.
探究新知
如图,AD⊥CD,BE⊥AF于B,CF⊥AF,在△ABC中,
BC边上的高是 ,在△AFC中CF边上的高是 .
例题讲解
例题讲解
如图,AD⊥CD,BE⊥AF,CF⊥AF,在△ABC中,
BC边上的高是 ,在△AFC中CF边上的高是 .
例题讲解
AD
如图,AD⊥CD,BE⊥AF,CF⊥AF,在△ABC中,
BC边上的高是 ,在△AFC中CF边上的高是 .
从复杂图形中分离出目标图形
例题讲解
如图,AD⊥CD,BE⊥AF,CF⊥AF,在△ABC中,
BC边上的高是 ,在△AFC中CF边上的高是 .
AD
例题讲解
AF
AD
如图,AD⊥CD,BE⊥AF,CF⊥AF,在△ABC中,
BC边上的高是 ,在△AFC中CF边上的高是 .
三角形的中线可以得到线段的相等关系,
它还有什么作用?
BD=CD
探究新知
AH=AH
????△????????????=????△????????????
?
探究新知
1.三角形的中线定义;
2.任意三角形的三条中线交于一点,交点在三角形内部;
3.三角形的一条中线将这个三角形分成面积相等的两个三角形.
已知:如图,在△ABC中,点D,E分别为BC,
AD的中点,且 =16,则 = .
例题讲解
CE为△ACD的中线
BE为△ABD的中线
8
AD为△ABC的中线
1.三角形中的主要线段
2.准确作图,有助于对图形准确深入的研究
课堂小结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
中 线
角平分线
高 线
图 形
共 同 点
(1)都是线段,其中一个端点都是三角形的顶点;
(2)三角形的中线,角平分线,高线各有三条,并且它们所在的直线都交于一点.
用途举例
(1)得到相等的线段
(2)构造面积相等的三角形
得到相等的角
(1)得到线段间的垂直关系
(2)进行与面积有关的计算
课后作业
1.如图,已知AD为△ABC的中线,AE为△ABC的高线,且
AB=5cm, AC=3cm.
(1)求△ABD与△ACD的周长之差;
(2)判断△ABD与△ACD的面积关系.
课后作业
2.如图,△ABC中,AD⊥BC,CE⊥AB,BC=6,AD=4,AB=7.
求CE的长.
同学们再见!
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
