京改版八年级上册:12.4全等三角形 课件(65张PPT)
文档属性
| 名称 | 京改版八年级上册:12.4全等三角形 课件(65张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览










文档简介
全等三角形
初二年级 数学
形状相同
大小相同
全等三角形的定义:
能够完全重合的两个三角形叫做全等三角形.
用符号“≌”来表示,读作“全等于”.
讲授新知
形状相同
大小相同
能够完全重合的两个图形叫做全等形.
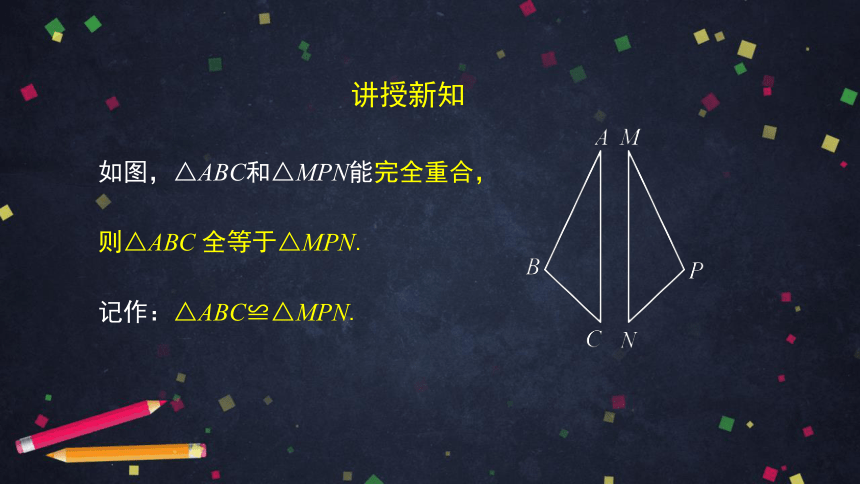
如图,△ABC和△MPN能完全重合,
讲授新知
则△ABC 全等于△MPN.
记作:△ABC≌△MPN.
讲授新知
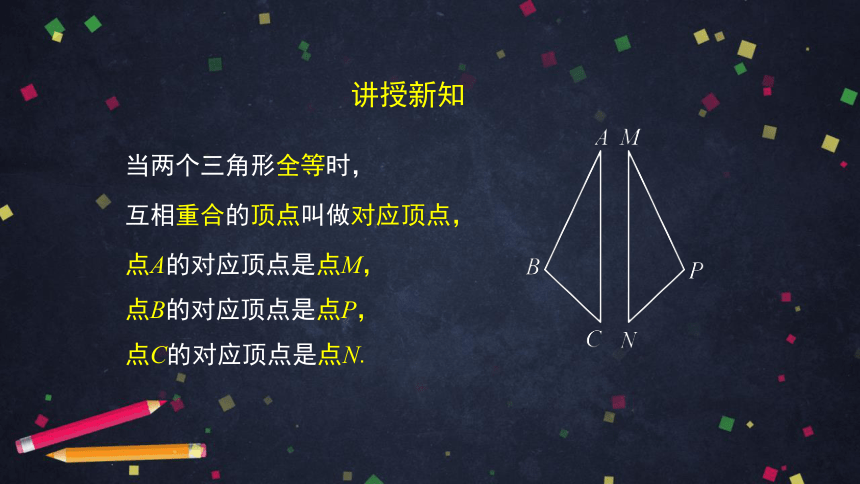
当两个三角形全等时,
互相重合的顶点叫做对应顶点,
点A的对应顶点是点M,
点B的对应顶点是点P,
点C的对应顶点是点N.
讲授新知
互相重合的边叫做对应边,
AB的对应边是MP,
BC的对应边是PN,
AC的对应边是MN.
讲授新知
互相重合的角叫做对应角,
∠A的对应角是∠M,
∠B的对应角是∠P,
∠C的对应角是∠N.
如图,△ABC和△MPN能完全重合
讲授新知
记作△ABC≌△MPN
按照对应关系书写
下图中,将△ABC平移至△DEF,则
△ABC≌ .并指出对应顶点、
对应边和对应角.
巩固新知
巩固新知
△ABC平移至△DEF
全等三角形的形成方式
找到重合的顶点、边和角
巩固新知
△ABC ≌ △DEF
巩固新知
点A的对应顶点是点D,
点B的对应顶点是点E,
点C的对应顶点是点F.
巩固新知
AB 的对应边是 DE,
BC 的对应边是 EF,
AC 的对应边是 DF.
巩固新知
∠A 的对应角是∠D,
∠B 的对应角是∠DEF,
∠ACB 的对应角是∠F.
巩固新知
≌
书写时,注意字母间的对应关系
△ABC ≌ △DEF
巩固新知
≌
书写时,注意字母间的对应关系
△ABC ≌ △DEF
巩固新知
2.下图中,将△ADC沿AC翻折至
△ABC,则△ABC≌ .
并指出对应顶点、对应边和
对应角.
△ABC≌△ADC
巩固新知
巩固新知
点A的对应顶点是点A,
点B的对应顶点是点D,
点C的对应顶点是点C.
巩固新知
AB 的对应边是 AD,
BC 的对应边是 DC,
AC 的对应边是 AC.
巩固新知
∠BAC 的对应角是∠DAC,
∠B 的对应角是∠D,
∠BCA 的对应角是∠DCA.
巩固新知
3.下图中,将△CBD绕
BD中点O旋转至△ABD,
则△ABD≌ .
并指出对应顶点、对应边
和对应角.
巩固新知
△ABD≌△CDB
巩固新知
点A的对应顶点是点C,
点B的对应顶点是点D,
点D的对应顶点是点B.
巩固新知
AB 的对应边是 CD,
BD 的对应边是 DB,
AD 的对应边是 CB.
巩固新知
∠A 的对应角是∠C,
∠ABD 的对应角是∠CDB,
∠ADB 的对应角是∠CBD.
阶段小结
1.寻找对应边、对应角的关键是能看出全等三角形的
形成方式和过程,进而找出对应的顶点、边和角;
2.通常情况下,在书写时应注意对应关系.
动手操作
摆一摆 试一试
请同学们利用手中全等三角形纸片尽可能多的摆
出不同的图形,并将摆好的图形画在纸上.
要求:全等三角形的对应边或对应角有重叠部分.
作品展示
作品展示
AB 的对应边是 AC,
AE 的对应边是 AD,
BE 的对应边是 CD.
作品展示
∠A 的对应角是∠A,
∠ABE 的对应角是∠ACD,
∠AEB 的对应角是∠ADC.
作品展示
作品展示
如图,两个三角形全等,
请找出对应边及对应角.
作品展示
AB 的对应边是 AD,
AC 的对应边是 AE,
BC 的对应边是 DE.
作品展示
∠BAC 的对应角是∠DAE,
∠B 的对应角是∠D,
∠C 的对应角是∠E.
作品展示
作品展示
如图,两个三角形全等,
请找出对应边及对应角.
作品展示
AB 的对应边是 AC,
AE 的对应边是 AD,
BE 的对应边是 CD.
作品展示
∠BAE 的对应角是∠CAD,
∠B 的对应角是∠C,
∠AEB 的对应角是∠ADC.
阶段小结
找对应边与对应角的常用方法:
1.可以通过观察三角形的构成元素(边或角)的特点,
找到对应边与对应角.
2.可以从图形变换的角度出发,观察图形平移、翻折、
旋转前后的对应关系,找到对应边与对应角.
探索性质
定义
判定
应用
研究几何图形的一般思路:
性质
探索性质
当两个三角形全等时,对应边、对应角
之间有怎样的数量关系?
能够完全重合的两个三角形叫做全等三角形
全等三角形的对应边相等
全等三角形的对应角相等
回顾定义
推出性质
△ABC≌△MPN
AB 的对应边是 MP,所以AB=MP.
BC 的对应边是 PN,所以BC=PN.
AC 的对应边是 MN,所以AC=MN.
探索性质
符号语言:
∵ △ABC≌△MPN,
∴ AB=MP,BC=PN,AC=MN.
(全等三角形的对应边相等)
探索性质
探索性质
△ABC≌△MPN
∠A 的对应角是∠M,所以∠A=∠M.
∠B 的对应角是∠P,所以∠B=∠P.
∠C 的对应角是∠N,所以∠C=∠N.
符号语言:
∵ △ABC≌△MPN,
∴ ∠A=∠M,∠B=∠P,∠C=∠N.
(全等三角形的对应角相等)
探索性质
例题讲解
例1 如图,△ABC≌△BAD,
AC与BD为对应边,
∠C与∠D为对应角,
AB=5,BD=6,AD=4,
则BC= .
例题讲解
AB=5,BD=6,AD=4
△BAD
△ABC
≌
BC=?
BC=AD
例题讲解
AB=5,BD=6,AD=4
△BAD
△ABC
≌
BC=AD
BC=4
例题讲解
例2 △DEC由△ABC绕着C点旋转得到,若∠ACB=75°,
∠ACD=25°,则∠ACE的度数是 .
例题讲解
△ABC≌△DEC
∠DCE =∠ACB=75°
∠ACE =∠DCE-∠DCA
= 75°-25°
= 50°
全等三角形的对应角相等
课堂小结
1.能够完全重合的两个三角形叫做全等三角形,
全等是两个三角形之间的一种特殊关系.
2.全等三角形的性质:
全等三角形对应边相等,
全等三角形对应角相等.
3.三角形经过平移、翻折、旋转后,虽然位置变了,但
形状和大小都没有改变,即平移、翻折、旋转前后的
三角形全等.
课堂小结
4.一般情况下找对应边与对应角的常用方法:
(1)有公共边的,公共边是对应边.
(2)有公共角的,公共角是对应角.
(3)有对顶角的,对顶角是对应角.
(4)两个全等三角形中,一对最长的边是对应边,
一对最短的边是对应边,角也是如此.
课堂小结
5.全等三角形带来边等及角等的条件,在分析问题时要注意
条件的侧重,及条件之间的相互转化,从而使分散的角或
边有联系,便于计算.
课堂小结
作业布置
1.如图,在两个全等三角形中,点A和点E是一组对应顶点,
请写出其他的对应顶点、对应边和对应角.
作业布置
2.如图,△ADF≌△CBE,AD与CB,DF与BE是对应边,
∠A=43°,∠B=50°,求∠D与∠BEC的度数.
作业布置
3.继续利用全等三角形纸片摆图形,找出对应边和对应角,
进一步体会图形的平移、翻折及旋转.
同学们再见!
初二年级 数学
形状相同
大小相同
全等三角形的定义:
能够完全重合的两个三角形叫做全等三角形.
用符号“≌”来表示,读作“全等于”.
讲授新知
形状相同
大小相同
能够完全重合的两个图形叫做全等形.
如图,△ABC和△MPN能完全重合,
讲授新知
则△ABC 全等于△MPN.
记作:△ABC≌△MPN.
讲授新知
当两个三角形全等时,
互相重合的顶点叫做对应顶点,
点A的对应顶点是点M,
点B的对应顶点是点P,
点C的对应顶点是点N.
讲授新知
互相重合的边叫做对应边,
AB的对应边是MP,
BC的对应边是PN,
AC的对应边是MN.
讲授新知
互相重合的角叫做对应角,
∠A的对应角是∠M,
∠B的对应角是∠P,
∠C的对应角是∠N.
如图,△ABC和△MPN能完全重合
讲授新知
记作△ABC≌△MPN
按照对应关系书写
下图中,将△ABC平移至△DEF,则
△ABC≌ .并指出对应顶点、
对应边和对应角.
巩固新知
巩固新知
△ABC平移至△DEF
全等三角形的形成方式
找到重合的顶点、边和角
巩固新知
△ABC ≌ △DEF
巩固新知
点A的对应顶点是点D,
点B的对应顶点是点E,
点C的对应顶点是点F.
巩固新知
AB 的对应边是 DE,
BC 的对应边是 EF,
AC 的对应边是 DF.
巩固新知
∠A 的对应角是∠D,
∠B 的对应角是∠DEF,
∠ACB 的对应角是∠F.
巩固新知
≌
书写时,注意字母间的对应关系
△ABC ≌ △DEF
巩固新知
≌
书写时,注意字母间的对应关系
△ABC ≌ △DEF
巩固新知
2.下图中,将△ADC沿AC翻折至
△ABC,则△ABC≌ .
并指出对应顶点、对应边和
对应角.
△ABC≌△ADC
巩固新知
巩固新知
点A的对应顶点是点A,
点B的对应顶点是点D,
点C的对应顶点是点C.
巩固新知
AB 的对应边是 AD,
BC 的对应边是 DC,
AC 的对应边是 AC.
巩固新知
∠BAC 的对应角是∠DAC,
∠B 的对应角是∠D,
∠BCA 的对应角是∠DCA.
巩固新知
3.下图中,将△CBD绕
BD中点O旋转至△ABD,
则△ABD≌ .
并指出对应顶点、对应边
和对应角.
巩固新知
△ABD≌△CDB
巩固新知
点A的对应顶点是点C,
点B的对应顶点是点D,
点D的对应顶点是点B.
巩固新知
AB 的对应边是 CD,
BD 的对应边是 DB,
AD 的对应边是 CB.
巩固新知
∠A 的对应角是∠C,
∠ABD 的对应角是∠CDB,
∠ADB 的对应角是∠CBD.
阶段小结
1.寻找对应边、对应角的关键是能看出全等三角形的
形成方式和过程,进而找出对应的顶点、边和角;
2.通常情况下,在书写时应注意对应关系.
动手操作
摆一摆 试一试
请同学们利用手中全等三角形纸片尽可能多的摆
出不同的图形,并将摆好的图形画在纸上.
要求:全等三角形的对应边或对应角有重叠部分.
作品展示
作品展示
AB 的对应边是 AC,
AE 的对应边是 AD,
BE 的对应边是 CD.
作品展示
∠A 的对应角是∠A,
∠ABE 的对应角是∠ACD,
∠AEB 的对应角是∠ADC.
作品展示
作品展示
如图,两个三角形全等,
请找出对应边及对应角.
作品展示
AB 的对应边是 AD,
AC 的对应边是 AE,
BC 的对应边是 DE.
作品展示
∠BAC 的对应角是∠DAE,
∠B 的对应角是∠D,
∠C 的对应角是∠E.
作品展示
作品展示
如图,两个三角形全等,
请找出对应边及对应角.
作品展示
AB 的对应边是 AC,
AE 的对应边是 AD,
BE 的对应边是 CD.
作品展示
∠BAE 的对应角是∠CAD,
∠B 的对应角是∠C,
∠AEB 的对应角是∠ADC.
阶段小结
找对应边与对应角的常用方法:
1.可以通过观察三角形的构成元素(边或角)的特点,
找到对应边与对应角.
2.可以从图形变换的角度出发,观察图形平移、翻折、
旋转前后的对应关系,找到对应边与对应角.
探索性质
定义
判定
应用
研究几何图形的一般思路:
性质
探索性质
当两个三角形全等时,对应边、对应角
之间有怎样的数量关系?
能够完全重合的两个三角形叫做全等三角形
全等三角形的对应边相等
全等三角形的对应角相等
回顾定义
推出性质
△ABC≌△MPN
AB 的对应边是 MP,所以AB=MP.
BC 的对应边是 PN,所以BC=PN.
AC 的对应边是 MN,所以AC=MN.
探索性质
符号语言:
∵ △ABC≌△MPN,
∴ AB=MP,BC=PN,AC=MN.
(全等三角形的对应边相等)
探索性质
探索性质
△ABC≌△MPN
∠A 的对应角是∠M,所以∠A=∠M.
∠B 的对应角是∠P,所以∠B=∠P.
∠C 的对应角是∠N,所以∠C=∠N.
符号语言:
∵ △ABC≌△MPN,
∴ ∠A=∠M,∠B=∠P,∠C=∠N.
(全等三角形的对应角相等)
探索性质
例题讲解
例1 如图,△ABC≌△BAD,
AC与BD为对应边,
∠C与∠D为对应角,
AB=5,BD=6,AD=4,
则BC= .
例题讲解
AB=5,BD=6,AD=4
△BAD
△ABC
≌
BC=?
BC=AD
例题讲解
AB=5,BD=6,AD=4
△BAD
△ABC
≌
BC=AD
BC=4
例题讲解
例2 △DEC由△ABC绕着C点旋转得到,若∠ACB=75°,
∠ACD=25°,则∠ACE的度数是 .
例题讲解
△ABC≌△DEC
∠DCE =∠ACB=75°
∠ACE =∠DCE-∠DCA
= 75°-25°
= 50°
全等三角形的对应角相等
课堂小结
1.能够完全重合的两个三角形叫做全等三角形,
全等是两个三角形之间的一种特殊关系.
2.全等三角形的性质:
全等三角形对应边相等,
全等三角形对应角相等.
3.三角形经过平移、翻折、旋转后,虽然位置变了,但
形状和大小都没有改变,即平移、翻折、旋转前后的
三角形全等.
课堂小结
4.一般情况下找对应边与对应角的常用方法:
(1)有公共边的,公共边是对应边.
(2)有公共角的,公共角是对应角.
(3)有对顶角的,对顶角是对应角.
(4)两个全等三角形中,一对最长的边是对应边,
一对最短的边是对应边,角也是如此.
课堂小结
5.全等三角形带来边等及角等的条件,在分析问题时要注意
条件的侧重,及条件之间的相互转化,从而使分散的角或
边有联系,便于计算.
课堂小结
作业布置
1.如图,在两个全等三角形中,点A和点E是一组对应顶点,
请写出其他的对应顶点、对应边和对应角.
作业布置
2.如图,△ADF≌△CBE,AD与CB,DF与BE是对应边,
∠A=43°,∠B=50°,求∠D与∠BEC的度数.
作业布置
3.继续利用全等三角形纸片摆图形,找出对应边和对应角,
进一步体会图形的平移、翻折及旋转.
同学们再见!
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
