京改版八年级上册12.5全等三角形的判定(1)课件(共37张ppt)
文档属性
| 名称 | 京改版八年级上册12.5全等三角形的判定(1)课件(共37张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 20:40:41 | ||
图片预览






文档简介
全等三角形的判定(1)
初二年级 数学
回顾全等三角形的定义
定义:能够完全重合的两个三角形叫做全等三角形.
思考:如果大家自己画出一个三角形,要满足什么条件,才能和其他同学画出的三角形完全重合呢?
如何能够唯一确定一个三角形的形状和大小?
给定△ABC
的形状和大小
AB,BC,AC
∠A,∠B,∠C
一个元素
两个元素
三个元素
……
探究
思考:给定三角形中的一个元素,我们能否唯一确定这个三角形的形状和大小?
?
一个元素
一边
一角
探究
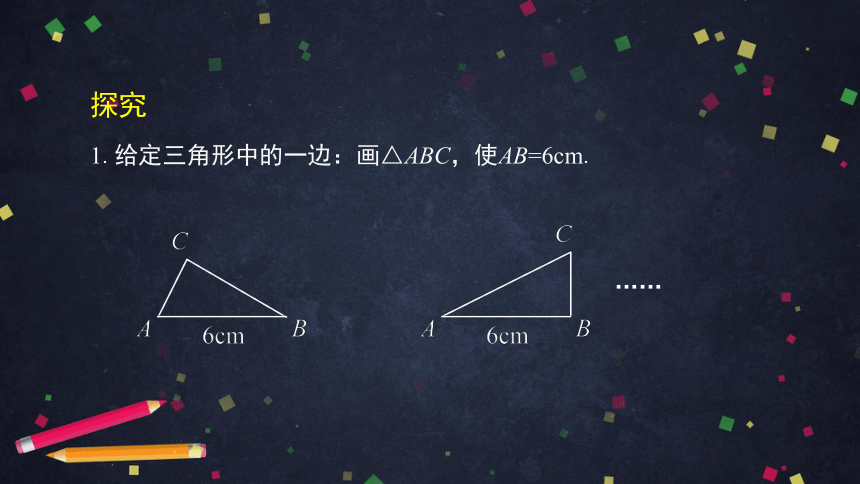
1.给定三角形中的一边:画△ABC,使AB=6cm.
……
探究
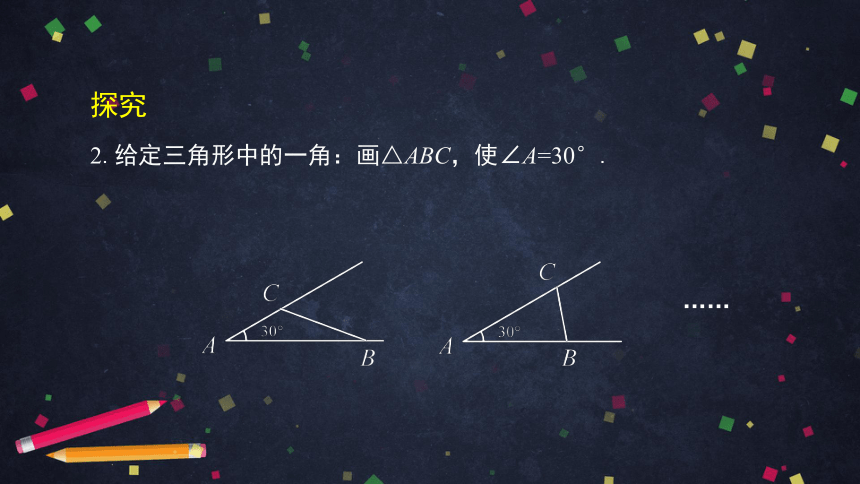
2.给定三角形中的一角:画△ABC,使∠A=30°.
……
探究
△ABC
AB,BC,AC
∠A,∠B,∠C
至少几个元素
确定
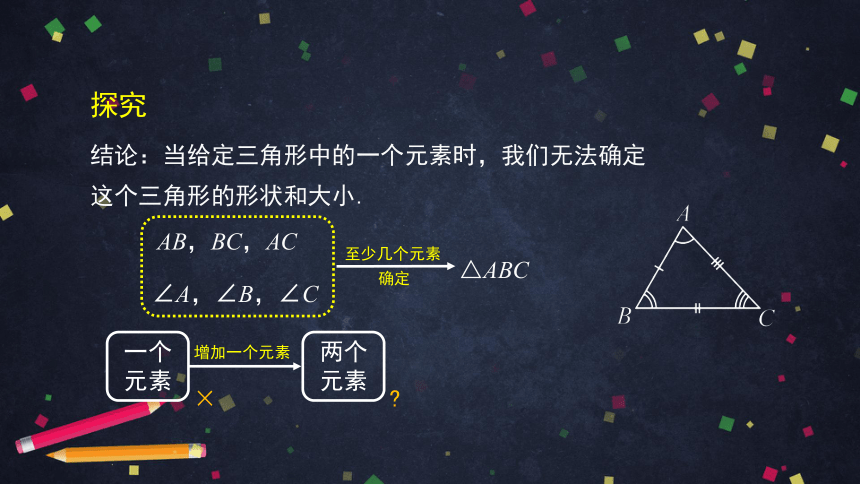
结论:当给定三角形中的一个元素时,我们无法确定
这个三角形的形状和大小.
一个元素
两个元素
×
增加一个元素
?
探究
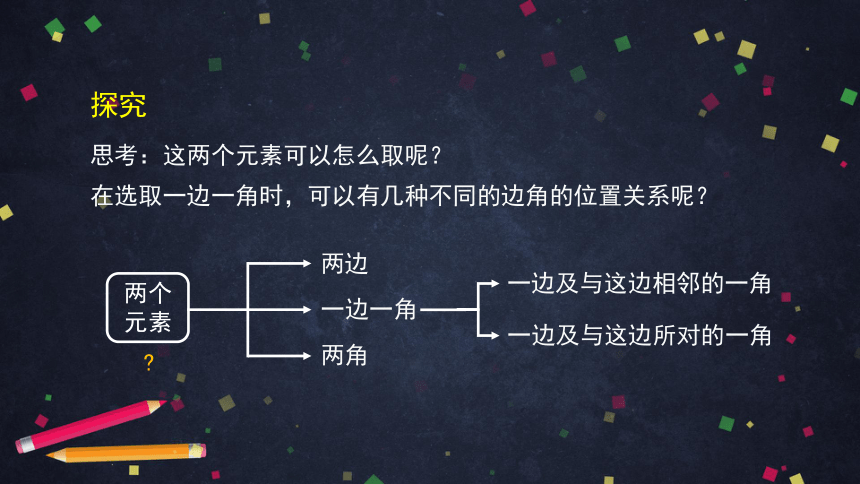
思考:这两个元素可以怎么取呢?
在选取一边一角时,可以有几种不同的边角的位置关系呢?
两个元素
两边
一边一角
一边及与这边相邻的一角
一边及与这边所对的一角
两角
?
探究
1.给定三角形中的两边:画△ABC,使AB=3cm,AC=4cm.
……
探究
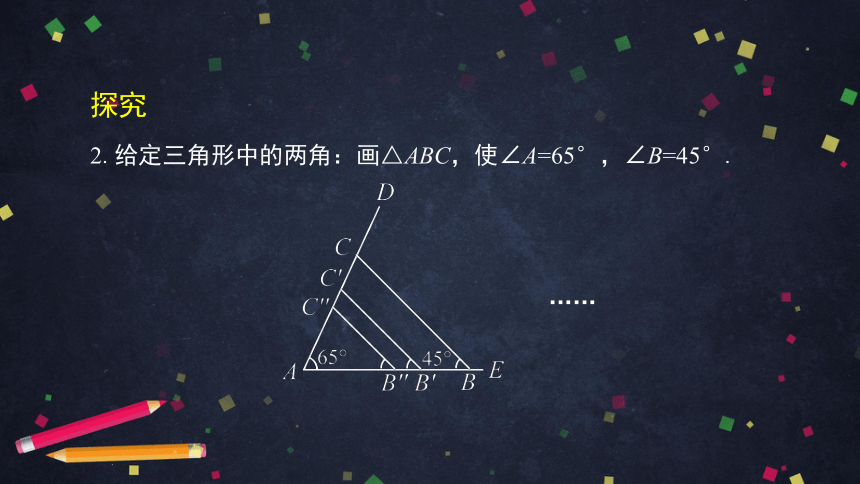
2.给定三角形中的两角:画△ABC,使∠A=65°,∠B=45°.
……
探究
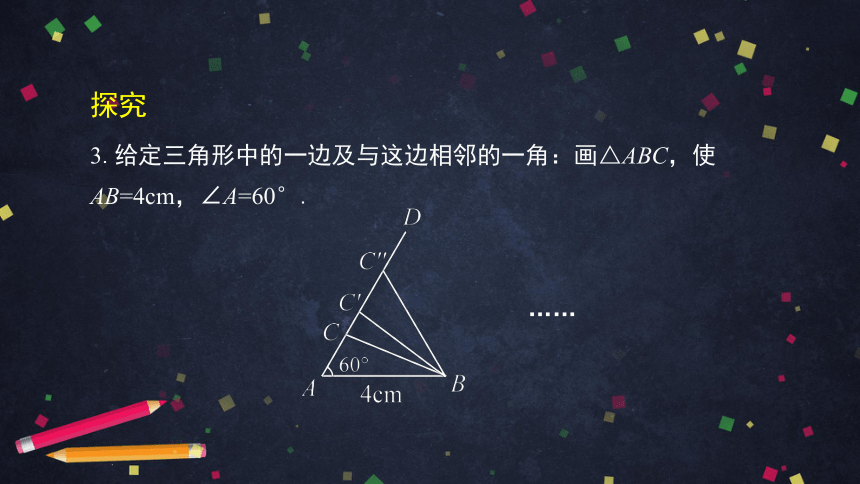
3.给定三角形中的一边及与这边相邻的一角:画△ABC,使AB=4cm,∠A=60°.
……
探究
4.给定三角形中的一边及与这边所对的一角:画△ABC,使BC=4cm,∠A=45°.
……
探究
△ABC
AB,BC,AC
∠A,∠B,∠C
至少几个元素
确定
一个元素
结论:当给定三角形中的两个元素时,我们还是无法确定
这个三角形的形状和大小.
两个元素
×
增加一个元素
?
三个元素
增加一个元素
×
探究
思考:这三个元素可以怎么取呢?
同学们想一想,这四种情况中是否有无需再进行探究的情况呢?
三个元素
两边一角
一边两角
想要确定一个三角形的
形状和大小,
至少要有一条边的条件
三角
?
三边
两角
探究
1.给定三角形中的三边:画△ABC,使AB=8cm,BC=4cm,
AC=6cm.
步骤:
(1)用直尺画出AB=8cm.
(2)用两把直尺固定另外两条边的边长,
分别为6cm,4cm,另外两边交于点C.
(3)分别连接AC,BC.
探究
1.给定三角形中的三边:画△ABC,使AB=8cm,BC=4cm,
AC=6cm.
探究
1.给定三角形中的三边:画△ABC,使AB=8cm,BC=4cm,
AC=6cm.
探究
1.给定三角形中的三边:画△ABC,使AB=8cm,BC=4cm,
AC=6cm.
探究
1.给定三角形中的三边:画△ABC,使AB=8cm,BC=4cm,
AC=6cm.
探究
1.给定三角形中的三边:画△ABC,使AB=8cm,BC=4cm,
AC=6cm.
一个元素
两个元素
×
增加一个元素
√
三个元素
增加一个元素
×
三边
△ABC的形状和大小
AB,BC,AC
唯一确定
三角形的稳定性
结论:如果给定大家三角形的三条边的长度,我们自己画出的一个三角形,都能和其他同学画出的三角形完全重合!
全等三角形的判定方法——边边边
三边分别相等的两个三角形全等(简记为“边边边”或“SSS”).
∴△ABC≌△DEF(SSS).
AB=DE,
BC=EF,
AC=DF,
在△ABC和△DEF中,
锁定目标
摆齐条件
得出结论
例 已知:如图,AB=AC,D为BC中点.
求证:△ABD≌△ACD.
△ABD与△ACD
AB=AC
BD=CD
AD=AD
D为BC中点
公共边AD
分析:
∴△ABD≌△ACD(SSS).
AB=AC,
BD=CD,
AD=AD,
准备条件
证明:∵D为BC中点,
∴BD=CD.
在△ABD和△ACD中,
锁定目标
摆齐条件
得出结论
例 已知:如图,AB=CD,BC=AD.
求证:△ABC≌△CDA.
△ABC与△CDA
分析:
由已知
想可知
AB=CD
BC=DA
AC=CA
公共边AC
例 已知:如图,AB=CD,BC=AD.
求证:△ABC≌△CDA.
∴△ABC≌△CDA(SSS).
AB=CD,
BC=DA,
AC=CA,
证明:在△ABC和△CDA中,
已知:如图,点A,E,F,C在一条直线上,AD=BC,DF=BE,AE=CF.
求证:△ADF≌△CBE.
由未知
想需知
△ADF≌△CBE?
分析:
AD=CB
DF=BE
AF=CE
AE=CF
公共部分EF
AF+EF=CE+EF
∴△ADF≌△CBE(SSS).
AD=CB,
DF=BE,
AF=CE,
证明:∵AE=CF,
∴AE+EF=CF+EF.
即AF=CE.
在△ADF和△CBE中,
准备条件
锁定目标
摆齐条件
得出结论
例 已知:如图,点B,C,F,E在一条直线上,AB=DE,AC=DF,BF=CE.
求证:△ABC≌△DEF.
由未知
想需知
△ABC≌△DEF?
分析:
AB=DE
AC=DF
BC=EF
BF=CE
公共部分CF
BF-CF=CE-CF
由已知
想可知
∴△ABC≌△DEF(SSS).
AB=DE,
AC=DF,
BC=EF,
证明:∵BF=CE,
∴BF-CF=CE-CF.
即BC=EF.
在△ABC和△DEF中,
准备条件
锁定目标
摆齐条件
得出结论
∵BF=CE,
∴BF-CF=CE-CF.
即BC=EF.
∵AE=CF,
∴AE+EF=CF+EF.
即AF=CE.
∵D为BC中点,
∴BD=CD.
证明线段相等的方法
全等三角形的定义
判定两个三角形全等的方法
课堂小结
画图探究
基本事实 SSS
完全重合
三边分别相等的两个三角形全等(简记为“边边边”或“SSS”).
∴△ABD≌△ACD(SSS).
AB=AC,
BD=CD,
AD=AD,
准备条件
证明:∵D为BC中点,
∴BD=CD.
在△ABD和△ACD中,
锁定目标
摆齐条件
得出结论
课堂小结
一个元素
两个元素
三个元素
……
一边
一角
两边
一边一角
两角
三边
两边一角
一边两角
?
形状大小唯一
√
边边边
×
×
课堂小结
作业1
已知:如图,AB=AD,CB=CD.
求证:△ABC≌△ADC.
作业2
已知:如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
求证:△ABC≌△DEF.
同学们再见!
初二年级 数学
回顾全等三角形的定义
定义:能够完全重合的两个三角形叫做全等三角形.
思考:如果大家自己画出一个三角形,要满足什么条件,才能和其他同学画出的三角形完全重合呢?
如何能够唯一确定一个三角形的形状和大小?
给定△ABC
的形状和大小
AB,BC,AC
∠A,∠B,∠C
一个元素
两个元素
三个元素
……
探究
思考:给定三角形中的一个元素,我们能否唯一确定这个三角形的形状和大小?
?
一个元素
一边
一角
探究
1.给定三角形中的一边:画△ABC,使AB=6cm.
……
探究
2.给定三角形中的一角:画△ABC,使∠A=30°.
……
探究
△ABC
AB,BC,AC
∠A,∠B,∠C
至少几个元素
确定
结论:当给定三角形中的一个元素时,我们无法确定
这个三角形的形状和大小.
一个元素
两个元素
×
增加一个元素
?
探究
思考:这两个元素可以怎么取呢?
在选取一边一角时,可以有几种不同的边角的位置关系呢?
两个元素
两边
一边一角
一边及与这边相邻的一角
一边及与这边所对的一角
两角
?
探究
1.给定三角形中的两边:画△ABC,使AB=3cm,AC=4cm.
……
探究
2.给定三角形中的两角:画△ABC,使∠A=65°,∠B=45°.
……
探究
3.给定三角形中的一边及与这边相邻的一角:画△ABC,使AB=4cm,∠A=60°.
……
探究
4.给定三角形中的一边及与这边所对的一角:画△ABC,使BC=4cm,∠A=45°.
……
探究
△ABC
AB,BC,AC
∠A,∠B,∠C
至少几个元素
确定
一个元素
结论:当给定三角形中的两个元素时,我们还是无法确定
这个三角形的形状和大小.
两个元素
×
增加一个元素
?
三个元素
增加一个元素
×
探究
思考:这三个元素可以怎么取呢?
同学们想一想,这四种情况中是否有无需再进行探究的情况呢?
三个元素
两边一角
一边两角
想要确定一个三角形的
形状和大小,
至少要有一条边的条件
三角
?
三边
两角
探究
1.给定三角形中的三边:画△ABC,使AB=8cm,BC=4cm,
AC=6cm.
步骤:
(1)用直尺画出AB=8cm.
(2)用两把直尺固定另外两条边的边长,
分别为6cm,4cm,另外两边交于点C.
(3)分别连接AC,BC.
探究
1.给定三角形中的三边:画△ABC,使AB=8cm,BC=4cm,
AC=6cm.
探究
1.给定三角形中的三边:画△ABC,使AB=8cm,BC=4cm,
AC=6cm.
探究
1.给定三角形中的三边:画△ABC,使AB=8cm,BC=4cm,
AC=6cm.
探究
1.给定三角形中的三边:画△ABC,使AB=8cm,BC=4cm,
AC=6cm.
探究
1.给定三角形中的三边:画△ABC,使AB=8cm,BC=4cm,
AC=6cm.
一个元素
两个元素
×
增加一个元素
√
三个元素
增加一个元素
×
三边
△ABC的形状和大小
AB,BC,AC
唯一确定
三角形的稳定性
结论:如果给定大家三角形的三条边的长度,我们自己画出的一个三角形,都能和其他同学画出的三角形完全重合!
全等三角形的判定方法——边边边
三边分别相等的两个三角形全等(简记为“边边边”或“SSS”).
∴△ABC≌△DEF(SSS).
AB=DE,
BC=EF,
AC=DF,
在△ABC和△DEF中,
锁定目标
摆齐条件
得出结论
例 已知:如图,AB=AC,D为BC中点.
求证:△ABD≌△ACD.
△ABD与△ACD
AB=AC
BD=CD
AD=AD
D为BC中点
公共边AD
分析:
∴△ABD≌△ACD(SSS).
AB=AC,
BD=CD,
AD=AD,
准备条件
证明:∵D为BC中点,
∴BD=CD.
在△ABD和△ACD中,
锁定目标
摆齐条件
得出结论
例 已知:如图,AB=CD,BC=AD.
求证:△ABC≌△CDA.
△ABC与△CDA
分析:
由已知
想可知
AB=CD
BC=DA
AC=CA
公共边AC
例 已知:如图,AB=CD,BC=AD.
求证:△ABC≌△CDA.
∴△ABC≌△CDA(SSS).
AB=CD,
BC=DA,
AC=CA,
证明:在△ABC和△CDA中,
已知:如图,点A,E,F,C在一条直线上,AD=BC,DF=BE,AE=CF.
求证:△ADF≌△CBE.
由未知
想需知
△ADF≌△CBE?
分析:
AD=CB
DF=BE
AF=CE
AE=CF
公共部分EF
AF+EF=CE+EF
∴△ADF≌△CBE(SSS).
AD=CB,
DF=BE,
AF=CE,
证明:∵AE=CF,
∴AE+EF=CF+EF.
即AF=CE.
在△ADF和△CBE中,
准备条件
锁定目标
摆齐条件
得出结论
例 已知:如图,点B,C,F,E在一条直线上,AB=DE,AC=DF,BF=CE.
求证:△ABC≌△DEF.
由未知
想需知
△ABC≌△DEF?
分析:
AB=DE
AC=DF
BC=EF
BF=CE
公共部分CF
BF-CF=CE-CF
由已知
想可知
∴△ABC≌△DEF(SSS).
AB=DE,
AC=DF,
BC=EF,
证明:∵BF=CE,
∴BF-CF=CE-CF.
即BC=EF.
在△ABC和△DEF中,
准备条件
锁定目标
摆齐条件
得出结论
∵BF=CE,
∴BF-CF=CE-CF.
即BC=EF.
∵AE=CF,
∴AE+EF=CF+EF.
即AF=CE.
∵D为BC中点,
∴BD=CD.
证明线段相等的方法
全等三角形的定义
判定两个三角形全等的方法
课堂小结
画图探究
基本事实 SSS
完全重合
三边分别相等的两个三角形全等(简记为“边边边”或“SSS”).
∴△ABD≌△ACD(SSS).
AB=AC,
BD=CD,
AD=AD,
准备条件
证明:∵D为BC中点,
∴BD=CD.
在△ABD和△ACD中,
锁定目标
摆齐条件
得出结论
课堂小结
一个元素
两个元素
三个元素
……
一边
一角
两边
一边一角
两角
三边
两边一角
一边两角
?
形状大小唯一
√
边边边
×
×
课堂小结
作业1
已知:如图,AB=AD,CB=CD.
求证:△ABC≌△ADC.
作业2
已知:如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
求证:△ABC≌△DEF.
同学们再见!
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
