京改版八年级上册第十一章实数和二次根式复习课件(共36张ppt)
文档属性
| 名称 | 京改版八年级上册第十一章实数和二次根式复习课件(共36张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 846.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 20:47:11 | ||
图片预览






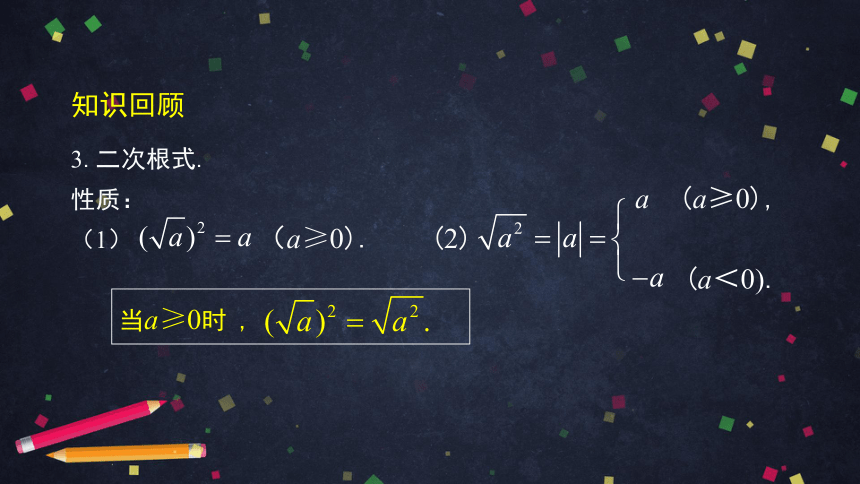

文档简介
实数和二次根式复习
初二年级 数学
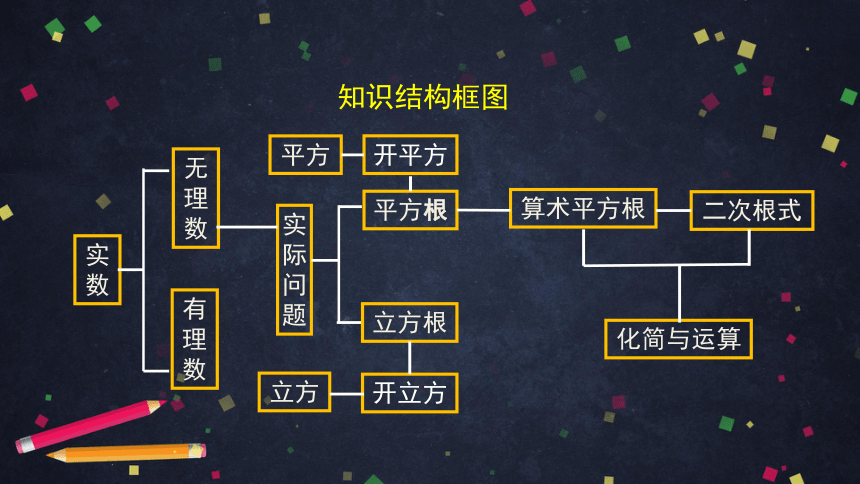
知识结构框图
实数
有理数
无理数
实际问题
平方根
开立方
算术平方根
二次根式
化简与运算
立方根
开平方
立方
平方
知识回顾
1.平方根、算数平方根、立方根.
平方根的概念:
算术平方根:
立方根的概念:
如果 x2=a ,那么x 叫做a 的平方根.
正数a 的正的平方根,叫做a 的算数平方根.
如果 x3=a,那么x 叫做a 的立方根.
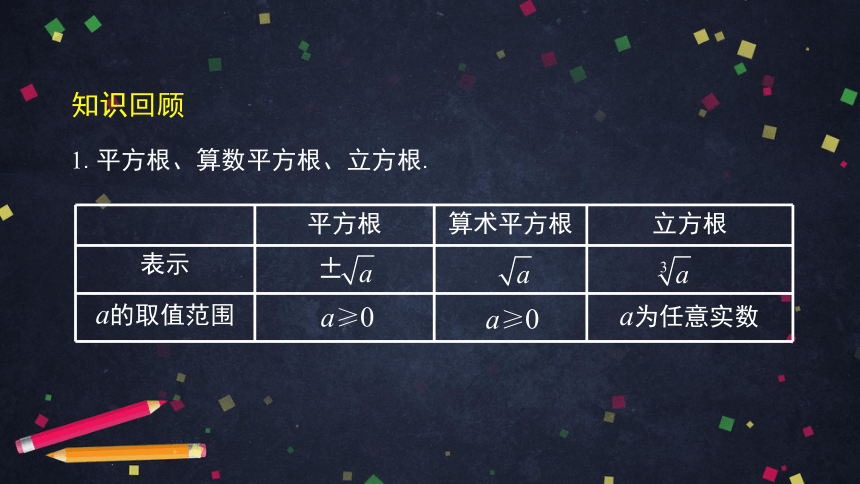
1.平方根、算数平方根、立方根.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
平方根
算术平方根
立方根
表示
a的取值范围
±
a≥0
a≥0
a为任意实数
知识回顾
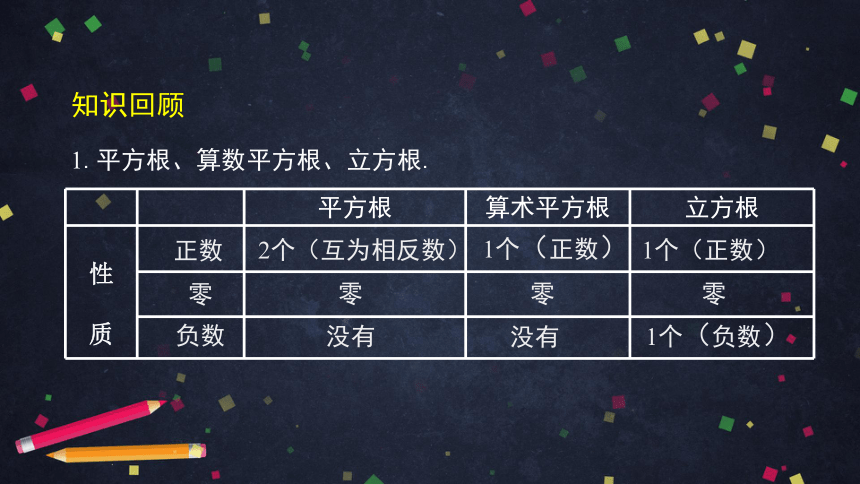
1.平方根、算数平方根、立方根.
平方根
算术平方根
立方根
性
质
2个(互为相反数)
1个(正数)
1个(正数)
1个(负数)
没有
没有
零
零
零
正数
负数
零
知识回顾
无理数的概念
实数的概念
实数与数轴
无限不循环小数叫做无理数
有理数和无理数统称为实数
实数和数轴上的点是一一对应的
知识回顾
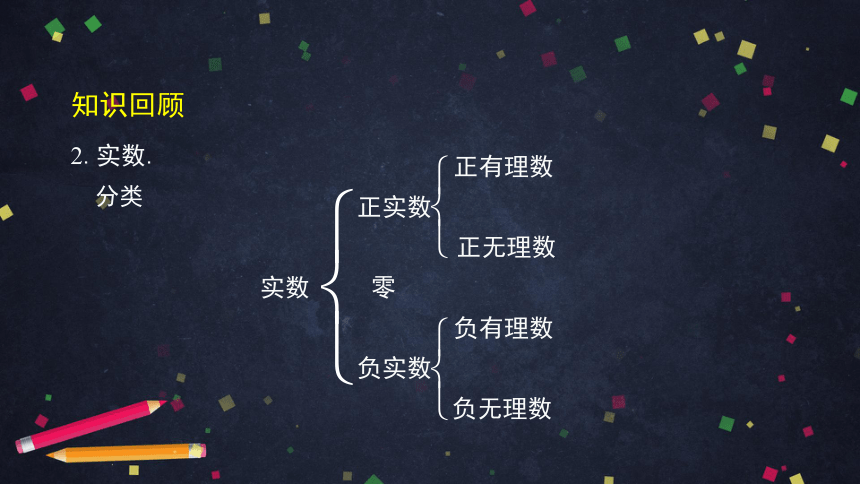
2.实数.
分类
正有理数
有理数 零
负有理数
实数
正无理数
无理数
负无理数
2.实数.
分类
知识回顾
正有理数
正实数
正无理数
实数 零
负有理数
负实数
负无理数
2.实数.
分类
知识回顾
3.二次根式.(概念)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}二次根式
最简二次根式
式子 (a≥0)
叫做二次根式.
满足两个条件:
(1)被开方数不含能开得尽方的因数或因式;
(2)被开方数的因数是整数,字母因式是整式 .
知识回顾
3.二次根式.(概念)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}二次根式
同类二次根式
式子 (a≥0)
叫做二次根式 .
几个二次根式分别化成最简二次根式以后,如果
被开方数相同,就把这几个二次根式叫做同类二次根式 .
知识回顾
3.二次根式.
性质: a (a≥0),
(1) (a≥0). (2)
(a<0).
当a≥0时 ,
知识回顾
3.二次根式.(运算)
加减法:先化成最简二次根式,再合并同类二次根式.
乘除法: (a≥0,b≥0),
(a≥0,b>0).
知识回顾
3.二次根式.(化简)
把乘除法法则的两个等式反过来写.
(a≥0,b≥0),
(a≥0,b>0).
知识回顾
例1 判断题:
(1) 的平方根是±3; ( )
(2) ; ( )
(3)8的立方根是2和-2; ( )
(4) ,0.571 4, 0.101 001 000 1…, 都是无理数;( )
(5)数轴上的每一个点都表示唯一的一个实数. ( )
例题讲解
例1 判断题:
(1) 的平方根是±3; ( )
3的平方根是
例题讲解
例1 判断题:
(2) ; ( )
例题讲解
例1 判断题:
(3)8的立方根是2和-2; ( )
8的立方根表示为
例题讲解
例1 判断题:
(4) ,0.571 4 , 0.101 001 000 1… ,
都是无理数; ( )
例题讲解
例1 判断题:
(5)数轴上的每一个点都表示唯一的一个实数. ( )
实数和数轴上的点是一一对应的
例题讲解
学习概念时要抓住本质, 不受表面形式的干扰.
判断一个数是否是无理数,不能看这个数是否含有根号.
, , 是有理数;
-0.101 001 000 1… , 是无理数.
归纳小结
例2 实数x在什么范围内取值时,下列各式有意义?
(1) ; (2) .
例题讲解
例2 实数x在什么范围内取值时,下列各式有意义?
(1) ;
分析:被开方数大于或等于零.
2x–1≥0.
例题讲解
例2 实数x在什么范围内取值时,下列各式有意义?
(1) ;
解:由2x–1≥0,得
x≥ .
所以当x≥ 时, 有意义.
例题讲解
(2) .
分析:
需要满足被开方数大于或等于0,也就是3–2x≥0,
分母不等于0,也就是 x–1≠0 ,两个条件同时满足 .
例题讲解
(2) .
解: (2)由 ≥0且 ,得 x≤ 且 .
所以当 x≤ 且 时, 有意义.
例题讲解
例3 计算:
(1) ; (2) .
例题讲解
例3 计算: (1)
分析:
先化简二次根式,
再合并同类二次根式.
例题讲解
例3 计算: (1)
解:
例题讲解
例3 计算:
解:
例题讲解
例3 计算:
方法二:
分析:
例题讲解
例3 计算:
解:
例题讲解
1.概念的学习要抓住本质,注意比较相近概念的相同点和不同点.
2.注意公式、法则的使用条件及正用、逆用.
3.类比的学习方法.
课堂小结
1.判断题:
(1) 7的算数平方根是 ; ( )
(2) 带根号的数都是无理数; ( )
(3) 1的平方根与立方根相等; ( )
(4) 无限小数都是无理数; ( )
(5)27的立方根是±3. ( )
课后练习
2.实数x在什么范围内取值时,下列各式有意义?
(1) ; (2) .
课后练习
3.计算:
(1) ; (2) .
课后练习
祝同学们学习进步!
初二年级 数学
知识结构框图
实数
有理数
无理数
实际问题
平方根
开立方
算术平方根
二次根式
化简与运算
立方根
开平方
立方
平方
知识回顾
1.平方根、算数平方根、立方根.
平方根的概念:
算术平方根:
立方根的概念:
如果 x2=a ,那么x 叫做a 的平方根.
正数a 的正的平方根,叫做a 的算数平方根.
如果 x3=a,那么x 叫做a 的立方根.
1.平方根、算数平方根、立方根.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
平方根
算术平方根
立方根
表示
a的取值范围
±
a≥0
a≥0
a为任意实数
知识回顾
1.平方根、算数平方根、立方根.
平方根
算术平方根
立方根
性
质
2个(互为相反数)
1个(正数)
1个(正数)
1个(负数)
没有
没有
零
零
零
正数
负数
零
知识回顾
无理数的概念
实数的概念
实数与数轴
无限不循环小数叫做无理数
有理数和无理数统称为实数
实数和数轴上的点是一一对应的
知识回顾
2.实数.
分类
正有理数
有理数 零
负有理数
实数
正无理数
无理数
负无理数
2.实数.
分类
知识回顾
正有理数
正实数
正无理数
实数 零
负有理数
负实数
负无理数
2.实数.
分类
知识回顾
3.二次根式.(概念)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}二次根式
最简二次根式
式子 (a≥0)
叫做二次根式.
满足两个条件:
(1)被开方数不含能开得尽方的因数或因式;
(2)被开方数的因数是整数,字母因式是整式 .
知识回顾
3.二次根式.(概念)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}二次根式
同类二次根式
式子 (a≥0)
叫做二次根式 .
几个二次根式分别化成最简二次根式以后,如果
被开方数相同,就把这几个二次根式叫做同类二次根式 .
知识回顾
3.二次根式.
性质: a (a≥0),
(1) (a≥0). (2)
(a<0).
当a≥0时 ,
知识回顾
3.二次根式.(运算)
加减法:先化成最简二次根式,再合并同类二次根式.
乘除法: (a≥0,b≥0),
(a≥0,b>0).
知识回顾
3.二次根式.(化简)
把乘除法法则的两个等式反过来写.
(a≥0,b≥0),
(a≥0,b>0).
知识回顾
例1 判断题:
(1) 的平方根是±3; ( )
(2) ; ( )
(3)8的立方根是2和-2; ( )
(4) ,0.571 4, 0.101 001 000 1…, 都是无理数;( )
(5)数轴上的每一个点都表示唯一的一个实数. ( )
例题讲解
例1 判断题:
(1) 的平方根是±3; ( )
3的平方根是
例题讲解
例1 判断题:
(2) ; ( )
例题讲解
例1 判断题:
(3)8的立方根是2和-2; ( )
8的立方根表示为
例题讲解
例1 判断题:
(4) ,0.571 4 , 0.101 001 000 1… ,
都是无理数; ( )
例题讲解
例1 判断题:
(5)数轴上的每一个点都表示唯一的一个实数. ( )
实数和数轴上的点是一一对应的
例题讲解
学习概念时要抓住本质, 不受表面形式的干扰.
判断一个数是否是无理数,不能看这个数是否含有根号.
, , 是有理数;
-0.101 001 000 1… , 是无理数.
归纳小结
例2 实数x在什么范围内取值时,下列各式有意义?
(1) ; (2) .
例题讲解
例2 实数x在什么范围内取值时,下列各式有意义?
(1) ;
分析:被开方数大于或等于零.
2x–1≥0.
例题讲解
例2 实数x在什么范围内取值时,下列各式有意义?
(1) ;
解:由2x–1≥0,得
x≥ .
所以当x≥ 时, 有意义.
例题讲解
(2) .
分析:
需要满足被开方数大于或等于0,也就是3–2x≥0,
分母不等于0,也就是 x–1≠0 ,两个条件同时满足 .
例题讲解
(2) .
解: (2)由 ≥0且 ,得 x≤ 且 .
所以当 x≤ 且 时, 有意义.
例题讲解
例3 计算:
(1) ; (2) .
例题讲解
例3 计算: (1)
分析:
先化简二次根式,
再合并同类二次根式.
例题讲解
例3 计算: (1)
解:
例题讲解
例3 计算:
解:
例题讲解
例3 计算:
方法二:
分析:
例题讲解
例3 计算:
解:
例题讲解
1.概念的学习要抓住本质,注意比较相近概念的相同点和不同点.
2.注意公式、法则的使用条件及正用、逆用.
3.类比的学习方法.
课堂小结
1.判断题:
(1) 7的算数平方根是 ; ( )
(2) 带根号的数都是无理数; ( )
(3) 1的平方根与立方根相等; ( )
(4) 无限小数都是无理数; ( )
(5)27的立方根是±3. ( )
课后练习
2.实数x在什么范围内取值时,下列各式有意义?
(1) ; (2) .
课后练习
3.计算:
(1) ; (2) .
课后练习
祝同学们学习进步!
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
