京改版八年级数学上册11.4无理数与实数(2)课件(52张)
文档属性
| 名称 | 京改版八年级数学上册11.4无理数与实数(2)课件(52张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 19:38:49 | ||
图片预览








文档简介
无理数与实数(2)
初二年级 数学
{5940675A-B579-460E-94D1-54222C63F5DA}
概 念
无理数
无限不循环小数叫做无理数
能用数轴上的点表示
在数轴上表示
能用数轴上的点表示
复习回顾
整数和分数统称为有理数
有理数和无理数都是现实世界中客观存在的量的反映.
有理数
{5940675A-B579-460E-94D1-54222C63F5DA}
概 念
无理数
无限不循环小数叫做无理数
能用数轴上的点表示
在数轴上表示
能用数轴上的点表示
复习回顾
整数和分数统称为有理数
有理数
有理数和无理数都是现实世界中客观存在的量的反映.
{5940675A-B579-460E-94D1-54222C63F5DA}
概 念
无理数
无限不循环小数叫做无理数
能用数轴上的点表示
在数轴上表示
能用数轴上的点表示
复习回顾
整数和分数统称为有理数
有理数
有理数和无理数都是现实世界中客观存在的量的反映.
:有理数和无理数统称为实数.
实数的概念
有理数的分类
有理数与数轴的关系
有理数的相反数和绝对值
有理数的大小比较
有理数的运算
实数的分类
实数与数轴的关系
实数的相反数和绝对值
实数的大小比较
实数的运算
类比
探究
探究新知
有理数的分类
有理数与数轴的关系
有理数的相反数和绝对值
有理数的大小比较
有理数的运算
实数的分类
实数与数轴的关系
实数的相反数和绝对值
实数的大小比较
实数的运算
类比
探究
探究新知
:有理数和无理数统称为实数.
实数的概念
正分数
负分数
正整数
负整数
零
整数
分数
有理数
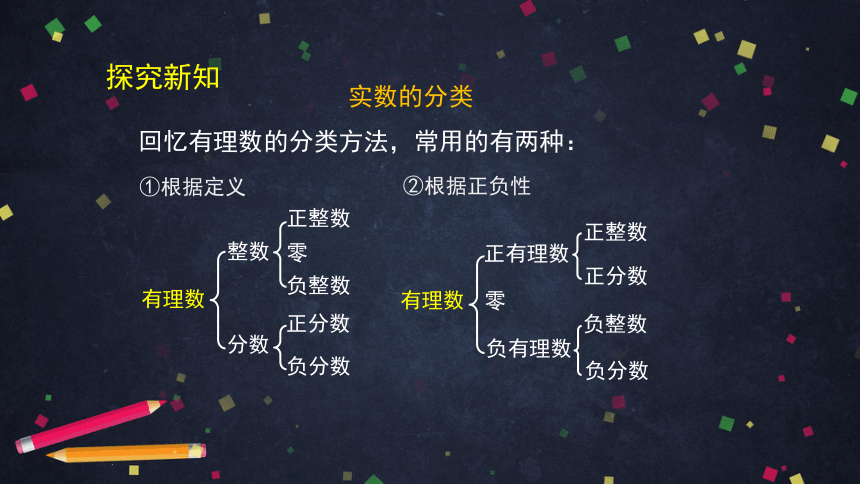
回忆有理数的分类方法,常用的有两种:
零
正有理数
负有理数
有理数
负整数
负分数
正整数
正分数
①根据定义
②根据正负性
实数的分类
探究新知
有理数
无理数
实数
正无理数
负无理数
正有理数
负有理数
零
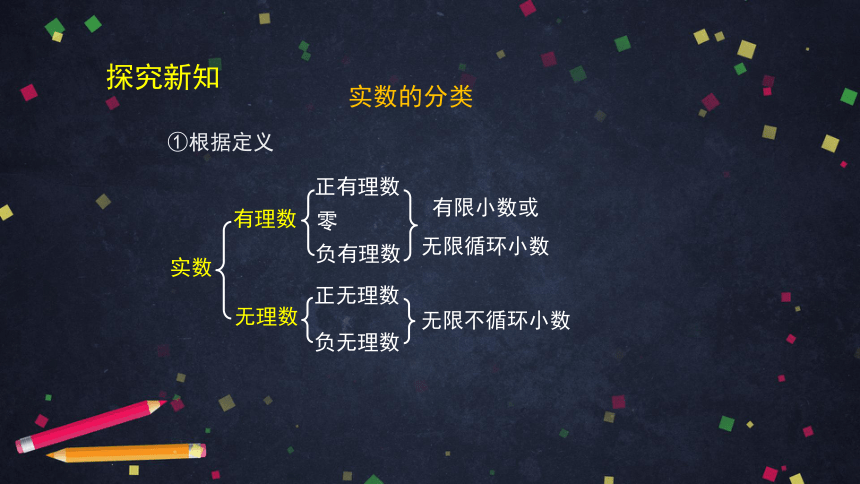
有限小数或
无限循环小数
无限不循环小数
探究新知
实数的分类
①根据定义
零
正实数
负实数
实数
负有理数
负无理数
正有理数
正无理数
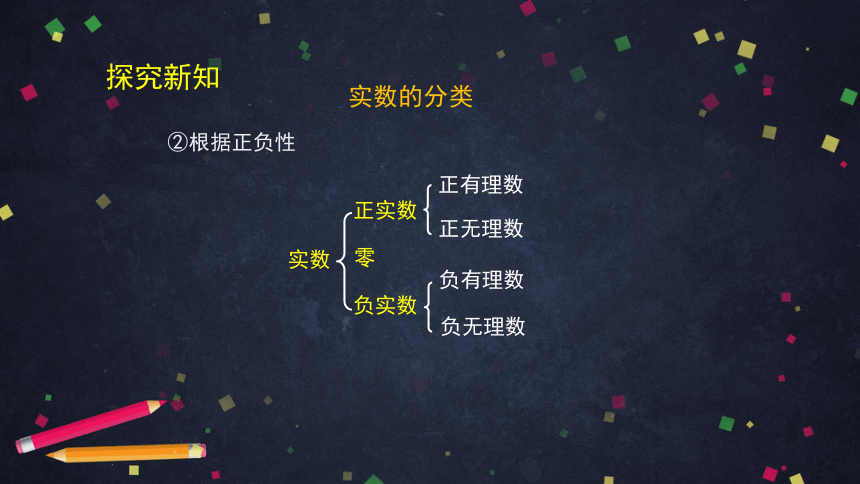
实数的分类
探究新知
②根据正负性
零
正实数
负实数
实数
负有理数
负无理数
正有理数
正无理数
正无理数
负无理数
正有理数
负有理数
零
有理数
无理数
实数
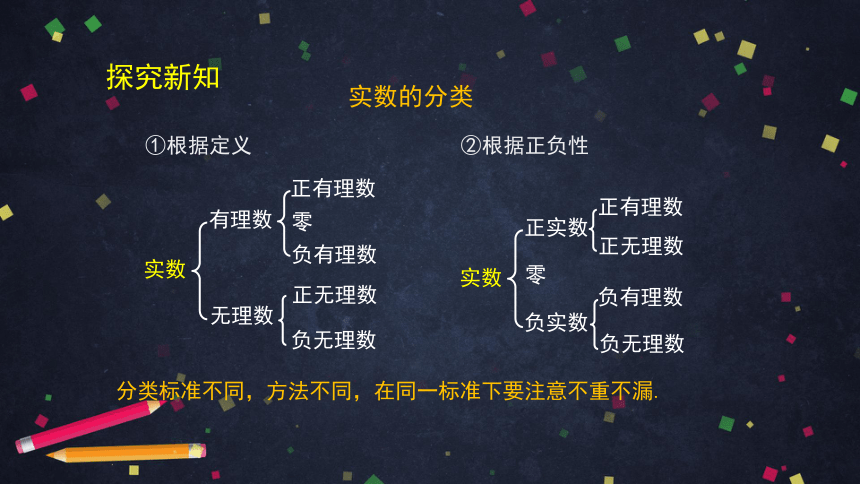
①根据定义
②根据正负性
分类标准不同,方法不同,在同一标准下要注意不重不漏.
探究新知
实数的分类
例1 已知下列各数:
整数有
有理数有
无理数有
实数有
;
;
;
.
例题讲解
例1 已知下列各数:
整数有
有理数有
无理数有
实数有
;
;
;
.
例题讲解
例1 已知下列各数:
整数有
有理数有
无理数有
实数有
;
;
;
.
例题讲解
例1 已知下列各数:
整数有
有理数有
无理数有
实数有
;
;
;
.
=?3
=0.5
例题讲解
无理数
例1 已知下列各数:
整数有
有理数有
无理数有
实数有
;
;
;
.
例题讲解
有理数的概念
有理数的分类
有理数与数轴的关系
有理数的相反数和绝对值
有理数的大小比较
有理数的运算
实数的概念
实数的分类
实数与数轴的关系
实数的相反数和绝对值
实数的大小比较
实数的运算
类比
探究
探究新知
0
1
2
3
-1
-2
-3
-4
4
M
如图,数轴上有一个点M,它所表示的数一定是有理数吗?
不一定,它所表示的数也可能是无理数.
探究新知
有理数和无理数都能用数轴上的点表示.这样,每一个实数都可以用数轴上唯一的一个点表示;反过来,数轴上的每一个点都表示唯一的一个实数.
实数和数轴上的点是一一对应的.
探究新知
实数与数轴的关系
实数
数轴上的点
数
形
数形结合
一一对应
探究新知
实数与数轴的关系
0
1
2
3
-1
-2
-3
-4
4
M
探究新知
有理数的概念
有理数的分类
有理数与数轴的关系
有理数的相反数和绝对值
有理数的大小比较
有理数的运算
实数的概念
实数的分类
实数与数轴的关系
实数的相反数和绝对值
实数的大小比较
实数的运算
类比
探究
探究新知
实数的相反数和绝对值
相反数的概念:
在数轴上,分布在原点的两侧,而且到原点的距离相等的两个点表示的数中,一个数叫做另一个数的相反数,或说它们互为相反数.
规定,0的相反数仍是0.
绝对值的概念:
数轴上表示数a的点到原点的距离叫做数a的绝对值.
规定,0的绝对值仍是0.
实数的相反数和绝对值的意义与在有理数范围内的意义是一样的.
实数的相反数和绝对值
探究新知
实数a的相反数是? .
探究新知
实数的相反数和绝对值
,
,
.
实数绝对值的求法
正实数的绝对值是它本身;
0的绝对值是0;
负实数的绝对值是它的相反数.
a
任何两个实数都是可以比较大小的,利用数轴可以直观地比较两个数的大小,数轴上右边的点总比左边的点表示的数大.
探究新知
实数的大小比较
0
1
2
3
-1
-2
-3
4
A
O
B
C
如图,A,B,C,O各点表示的数分别是π, ,?3,0.
把这4个实数按从小到大的顺序用不等号连接起来:
探究新知
实数的大小比较
正实数都 0,负实数都 0;正实数都 负
实数;两个负实数比较,绝对值大的反而 .
大于
小于
大于
小
探究新知
实数的大小比较
0
1
2
3
-1
-2
-3
-4
4
例2 (1)求实数 的相反数和绝对值;
(2)求绝对值为 的实数;
(3)比较无理数 和 的大小.
例题讲解
解: ;
∵
.
∴
的相反数是 ;
∴
例题讲解
例2 (1)求实数 的相反数和绝对值;
解:
,
,
∵
例2 (2)求绝对值为 的实数;
绝对值为 的实数是 .
∴
例题讲解
例2 (3)比较无理数 和 的大小.
解:
.
,
,
∵
.
∴
∴
例题讲解
探究新知
有理数的概念
有理数的分类
有理数与数轴的关系
有理数的相反数和绝对值
有理数的大小比较
有理数的运算
实数的概念
实数的分类
实数与数轴的关系
实数的相反数和绝对值
实数的大小比较
实数的运算
类比
探究
实数之间不仅可以进行加、减、乘、除(除数不为0)、乘方运算,而且正实数和0可以进行开平方运算,任意一个实数可以进行开立方运算.
探究新知
实数的运算
思考1:实数之间可以进行哪些运算?
实数可以按有理数的运算法则和运算律进行运算.
探究新知
实数的运算
思考2:在进行实数运算时,可以按有理数的运算法则和
运算律进行运算吗?
例3 计算:(1) ; (2) .
例题讲解
解:原式
(加法交换律)
(加法结合律)
例题讲解
例3 计算:(1) ;
;
解:原式
(乘法分配律的逆用)
例题讲解
例3 计算:(2) .
.
涉及无理数的近似计算时,可以根据问题的要求取其近似值,转化成有理数进行计算.
例题讲解
例4 近似计算(结果保留小数点后两位):
(1)
(2)
;
.
解:
注意使用“ ”符号
计算过程中取的近似值应比结果要求的至少多一位
例题讲解
例4 近似计算(结果保留小数点后两位):
(1)
;
;
例题讲解
例4 近似计算(结果保留小数点后两位):
(2)
.
.
计算过程中取的近似值应比结果要求的至少多一位
注意使用“ ”符号
解:
例5 某易拉罐饮料的罐上标有“净含量240mL”,量得它的高为12cm. 如果将它近似看成圆柱体,试求易拉罐的底面直径(结果精确到1cm,1mL=1cm3,圆柱体体积公式为
V=πR2h
实际应用
).
分析:
V=πR2h
无理数
表示圆柱体的体积V=240
表示圆柱体的高h=12
表示圆柱体的底面半径,是未知量
观察公式
例5 某易拉罐饮料的罐上标有“净含量240mL”,量得它的高为12cm. 如果将它近似看成圆柱体,试求易拉罐的底面直径(结果精确到1cm,1mL=1cm3,圆柱体体积公式为
V=πR2h
).
分析:
V=πR2h
无理数
表示圆柱体的体积V=240
表示圆柱体的高h=12
表示圆柱体的底面半径,是未知量
观察公式
实际应用
例5 某易拉罐饮料的罐上标有“净含量240mL”,量得它的高为12cm. 如果将它近似看成圆柱体,试求易拉罐的底面直径(结果精确到1cm,1mL=1cm3,圆柱体体积公式为
解:由题意得πR2 12=240,所以2R=2 ,
由计算器计算得 2R = 5.046 265 044…≈ 5
答:易拉罐的底面直径约为5cm.
.
).
V=πR2h
实际应用
强调两点:
1.实数可以按有理数的运算法则和运算律进行运算;
2.当实数运算中遇到无理数时,可根据问题的要求取其近似值,转化为有理数进行计算.
实数的运算
1. 求下列各实数的绝对值:
(2) .
(1)π ? 3.14;
巩固练习
1. 求下列各实数的绝对值:
(1)π ? 3.14;
解:
∵ π > 3.14 ,
∴ π?3.14 > 0
.
∴
巩固练习
,
(2) .
解:
,
,
.
∴
∴
∵
巩固练习
2. 用“>”、“<”或“=”填空:
;
;
.
<
约等于5.308
>
3.141…
>
3.142 857
.
.
巩固练习
约等于5.385
学习了实数的概念,分类,实数与数轴上的点一一对应,实数的相反数和绝对值,实数的大小比较以及简单的实数运算.
课堂小结
课堂小结
有理数的概念
有理数的分类
有理数与数轴的关系
有理数的相反数和绝对值
有理数的大小比较
有理数的运算
实数的概念
实数的分类
实数与数轴的关系
实数的相反数和绝对值
实数的大小比较
实数的运算
类比
探究
1. 下列各数中,哪些是有理数?哪些是无理数?哪些是实数?
2.“有理数和数轴上的点是一一对应的”,这个说法对吗?
为什么?
(两个2之间依次多一个1)
3.212 112 111 2….
课后练习
,
,
,
,
,
,
,
3. 求下列各实数的相反数和绝对值:
4. 两个无理数的和、差、积、商一定是无理数吗?举例说明.
课后练习
祝同学们学习进步!
初二年级 数学
{5940675A-B579-460E-94D1-54222C63F5DA}
概 念
无理数
无限不循环小数叫做无理数
能用数轴上的点表示
在数轴上表示
能用数轴上的点表示
复习回顾
整数和分数统称为有理数
有理数和无理数都是现实世界中客观存在的量的反映.
有理数
{5940675A-B579-460E-94D1-54222C63F5DA}
概 念
无理数
无限不循环小数叫做无理数
能用数轴上的点表示
在数轴上表示
能用数轴上的点表示
复习回顾
整数和分数统称为有理数
有理数
有理数和无理数都是现实世界中客观存在的量的反映.
{5940675A-B579-460E-94D1-54222C63F5DA}
概 念
无理数
无限不循环小数叫做无理数
能用数轴上的点表示
在数轴上表示
能用数轴上的点表示
复习回顾
整数和分数统称为有理数
有理数
有理数和无理数都是现实世界中客观存在的量的反映.
:有理数和无理数统称为实数.
实数的概念
有理数的分类
有理数与数轴的关系
有理数的相反数和绝对值
有理数的大小比较
有理数的运算
实数的分类
实数与数轴的关系
实数的相反数和绝对值
实数的大小比较
实数的运算
类比
探究
探究新知
有理数的分类
有理数与数轴的关系
有理数的相反数和绝对值
有理数的大小比较
有理数的运算
实数的分类
实数与数轴的关系
实数的相反数和绝对值
实数的大小比较
实数的运算
类比
探究
探究新知
:有理数和无理数统称为实数.
实数的概念
正分数
负分数
正整数
负整数
零
整数
分数
有理数
回忆有理数的分类方法,常用的有两种:
零
正有理数
负有理数
有理数
负整数
负分数
正整数
正分数
①根据定义
②根据正负性
实数的分类
探究新知
有理数
无理数
实数
正无理数
负无理数
正有理数
负有理数
零
有限小数或
无限循环小数
无限不循环小数
探究新知
实数的分类
①根据定义
零
正实数
负实数
实数
负有理数
负无理数
正有理数
正无理数
实数的分类
探究新知
②根据正负性
零
正实数
负实数
实数
负有理数
负无理数
正有理数
正无理数
正无理数
负无理数
正有理数
负有理数
零
有理数
无理数
实数
①根据定义
②根据正负性
分类标准不同,方法不同,在同一标准下要注意不重不漏.
探究新知
实数的分类
例1 已知下列各数:
整数有
有理数有
无理数有
实数有
;
;
;
.
例题讲解
例1 已知下列各数:
整数有
有理数有
无理数有
实数有
;
;
;
.
例题讲解
例1 已知下列各数:
整数有
有理数有
无理数有
实数有
;
;
;
.
例题讲解
例1 已知下列各数:
整数有
有理数有
无理数有
实数有
;
;
;
.
=?3
=0.5
例题讲解
无理数
例1 已知下列各数:
整数有
有理数有
无理数有
实数有
;
;
;
.
例题讲解
有理数的概念
有理数的分类
有理数与数轴的关系
有理数的相反数和绝对值
有理数的大小比较
有理数的运算
实数的概念
实数的分类
实数与数轴的关系
实数的相反数和绝对值
实数的大小比较
实数的运算
类比
探究
探究新知
0
1
2
3
-1
-2
-3
-4
4
M
如图,数轴上有一个点M,它所表示的数一定是有理数吗?
不一定,它所表示的数也可能是无理数.
探究新知
有理数和无理数都能用数轴上的点表示.这样,每一个实数都可以用数轴上唯一的一个点表示;反过来,数轴上的每一个点都表示唯一的一个实数.
实数和数轴上的点是一一对应的.
探究新知
实数与数轴的关系
实数
数轴上的点
数
形
数形结合
一一对应
探究新知
实数与数轴的关系
0
1
2
3
-1
-2
-3
-4
4
M
探究新知
有理数的概念
有理数的分类
有理数与数轴的关系
有理数的相反数和绝对值
有理数的大小比较
有理数的运算
实数的概念
实数的分类
实数与数轴的关系
实数的相反数和绝对值
实数的大小比较
实数的运算
类比
探究
探究新知
实数的相反数和绝对值
相反数的概念:
在数轴上,分布在原点的两侧,而且到原点的距离相等的两个点表示的数中,一个数叫做另一个数的相反数,或说它们互为相反数.
规定,0的相反数仍是0.
绝对值的概念:
数轴上表示数a的点到原点的距离叫做数a的绝对值.
规定,0的绝对值仍是0.
实数的相反数和绝对值的意义与在有理数范围内的意义是一样的.
实数的相反数和绝对值
探究新知
实数a的相反数是? .
探究新知
实数的相反数和绝对值
,
,
.
实数绝对值的求法
正实数的绝对值是它本身;
0的绝对值是0;
负实数的绝对值是它的相反数.
a
任何两个实数都是可以比较大小的,利用数轴可以直观地比较两个数的大小,数轴上右边的点总比左边的点表示的数大.
探究新知
实数的大小比较
0
1
2
3
-1
-2
-3
4
A
O
B
C
如图,A,B,C,O各点表示的数分别是π, ,?3,0.
把这4个实数按从小到大的顺序用不等号连接起来:
探究新知
实数的大小比较
正实数都 0,负实数都 0;正实数都 负
实数;两个负实数比较,绝对值大的反而 .
大于
小于
大于
小
探究新知
实数的大小比较
0
1
2
3
-1
-2
-3
-4
4
例2 (1)求实数 的相反数和绝对值;
(2)求绝对值为 的实数;
(3)比较无理数 和 的大小.
例题讲解
解: ;
∵
.
∴
的相反数是 ;
∴
例题讲解
例2 (1)求实数 的相反数和绝对值;
解:
,
,
∵
例2 (2)求绝对值为 的实数;
绝对值为 的实数是 .
∴
例题讲解
例2 (3)比较无理数 和 的大小.
解:
.
,
,
∵
.
∴
∴
例题讲解
探究新知
有理数的概念
有理数的分类
有理数与数轴的关系
有理数的相反数和绝对值
有理数的大小比较
有理数的运算
实数的概念
实数的分类
实数与数轴的关系
实数的相反数和绝对值
实数的大小比较
实数的运算
类比
探究
实数之间不仅可以进行加、减、乘、除(除数不为0)、乘方运算,而且正实数和0可以进行开平方运算,任意一个实数可以进行开立方运算.
探究新知
实数的运算
思考1:实数之间可以进行哪些运算?
实数可以按有理数的运算法则和运算律进行运算.
探究新知
实数的运算
思考2:在进行实数运算时,可以按有理数的运算法则和
运算律进行运算吗?
例3 计算:(1) ; (2) .
例题讲解
解:原式
(加法交换律)
(加法结合律)
例题讲解
例3 计算:(1) ;
;
解:原式
(乘法分配律的逆用)
例题讲解
例3 计算:(2) .
.
涉及无理数的近似计算时,可以根据问题的要求取其近似值,转化成有理数进行计算.
例题讲解
例4 近似计算(结果保留小数点后两位):
(1)
(2)
;
.
解:
注意使用“ ”符号
计算过程中取的近似值应比结果要求的至少多一位
例题讲解
例4 近似计算(结果保留小数点后两位):
(1)
;
;
例题讲解
例4 近似计算(结果保留小数点后两位):
(2)
.
.
计算过程中取的近似值应比结果要求的至少多一位
注意使用“ ”符号
解:
例5 某易拉罐饮料的罐上标有“净含量240mL”,量得它的高为12cm. 如果将它近似看成圆柱体,试求易拉罐的底面直径(结果精确到1cm,1mL=1cm3,圆柱体体积公式为
V=πR2h
实际应用
).
分析:
V=πR2h
无理数
表示圆柱体的体积V=240
表示圆柱体的高h=12
表示圆柱体的底面半径,是未知量
观察公式
例5 某易拉罐饮料的罐上标有“净含量240mL”,量得它的高为12cm. 如果将它近似看成圆柱体,试求易拉罐的底面直径(结果精确到1cm,1mL=1cm3,圆柱体体积公式为
V=πR2h
).
分析:
V=πR2h
无理数
表示圆柱体的体积V=240
表示圆柱体的高h=12
表示圆柱体的底面半径,是未知量
观察公式
实际应用
例5 某易拉罐饮料的罐上标有“净含量240mL”,量得它的高为12cm. 如果将它近似看成圆柱体,试求易拉罐的底面直径(结果精确到1cm,1mL=1cm3,圆柱体体积公式为
解:由题意得πR2 12=240,所以2R=2 ,
由计算器计算得 2R = 5.046 265 044…≈ 5
答:易拉罐的底面直径约为5cm.
.
).
V=πR2h
实际应用
强调两点:
1.实数可以按有理数的运算法则和运算律进行运算;
2.当实数运算中遇到无理数时,可根据问题的要求取其近似值,转化为有理数进行计算.
实数的运算
1. 求下列各实数的绝对值:
(2) .
(1)π ? 3.14;
巩固练习
1. 求下列各实数的绝对值:
(1)π ? 3.14;
解:
∵ π > 3.14 ,
∴ π?3.14 > 0
.
∴
巩固练习
,
(2) .
解:
,
,
.
∴
∴
∵
巩固练习
2. 用“>”、“<”或“=”填空:
;
;
.
<
约等于5.308
>
3.141…
>
3.142 857
.
.
巩固练习
约等于5.385
学习了实数的概念,分类,实数与数轴上的点一一对应,实数的相反数和绝对值,实数的大小比较以及简单的实数运算.
课堂小结
课堂小结
有理数的概念
有理数的分类
有理数与数轴的关系
有理数的相反数和绝对值
有理数的大小比较
有理数的运算
实数的概念
实数的分类
实数与数轴的关系
实数的相反数和绝对值
实数的大小比较
实数的运算
类比
探究
1. 下列各数中,哪些是有理数?哪些是无理数?哪些是实数?
2.“有理数和数轴上的点是一一对应的”,这个说法对吗?
为什么?
(两个2之间依次多一个1)
3.212 112 111 2….
课后练习
,
,
,
,
,
,
,
3. 求下列各实数的相反数和绝对值:
4. 两个无理数的和、差、积、商一定是无理数吗?举例说明.
课后练习
祝同学们学习进步!
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
