人教版 八年级数学下册 16.2 二次根式的乘除第二课时:二次根式的除法课件(20张)
文档属性
| 名称 | 人教版 八年级数学下册 16.2 二次根式的乘除第二课时:二次根式的除法课件(20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 227.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 19:38:45 | ||
图片预览







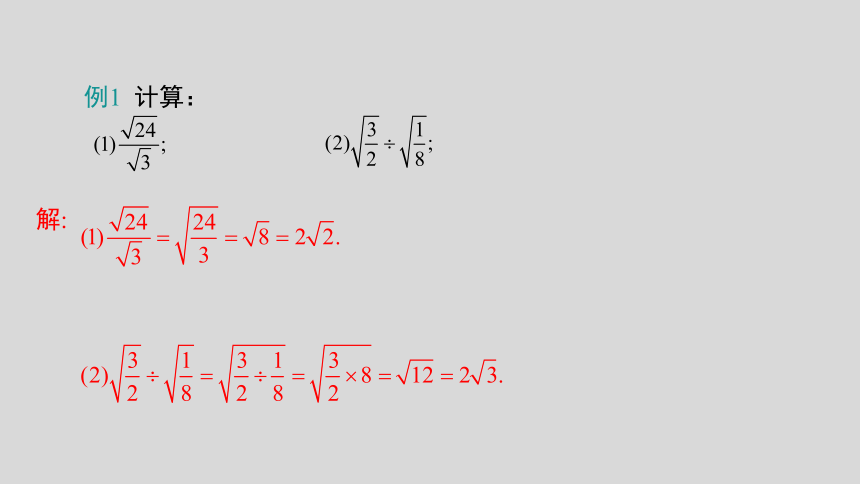

文档简介
16.2 二次根式的乘除
第2课时 二次根式的除法
(1)利用归纳类比的方法得出二次根式的除法法则和商的算术平方根的性质;
(2)会进行简单的二次根式的除法运算;
?(3) 理解最简二次根式的概念.
教学目标
复习提问,探究规律
二次根式的乘法法则是什么内容?化简二次根式的一般步骤怎样?
知识 1
二次根式除法的运算法则
2
3
=
=
=
=
思考 通过上述二次根式除法运算结果,联想到二次根式除法运算法则,你能说出二次根式 的结果吗?
两个二次根式相除,把被开方数相除,根指
数不变,即: (a≥0,b>0).
二次根式的除法法则:
文字叙述:
算术平方根的商等于被开方数商的算术平方根.
当二次根式根号外的因数(式)不为1时,可类比单项式除以单项式法则,易得
对比乘法法则里字母的取值范围,除法法则里字母的取值范围有何变化?
例1 计算:
解:
小结
利用二次根式的除法法则进行计算,被开方
数相除时,可以用“除以一个不为零的数等于乘这
个数的倒数”进行约分、化简.
1.计算
你有几种方法去掉分母中的根号?去分母的依据分别是什么? 再提问:第(2)题用什么方法计算更简捷?第(3)题根号下含字母在移出根号时应注意什么?
2.计算 的结果是__________.
3. 计算 的结果是( )
A. B. C. D.
知识 2
二次根式除法法则的逆运用
把 反过来,就得到
利用它可以进行二次根式的化简
二次根式的商的算术平方根的性质:
例2 化简:
解:
二次根式的运算结果有以下特点:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
知识 3
最简二次根式
简记为:一根号无分母,分母无根号;二不能再开方.
在二次根式的运算中,一般要把最后结果化为最简二次根式,并且分母中不含二次根式.
下列二次根式是否是最简二次根式?为什么?
例3
例4 设长方形的面积为S,相邻两边长分别为a,b.已知 ,求a的值.
学生独立思考写出答案,组内交流,小组展示
随堂检测
1 把下列二次根式化成最简二次根式:
(1) (2)
2.下列各式中,是最简二次根式的是( )
3.若使等式 成立,则实数k取值范围是 ( )
A.k≥1 B.k≥2
C. 1<k≤2 D. 1≤k≤2
4.已知xy<0,化简二次根式 的正确结果为( )
A. B.
C. D.
6.化简
归纳小结
共同回顾本节课所学内容,回答以下问题: (1)除法运算的法则如何?对等式中字母的取值范围有何要求? (2)你能说明最简二次根式需要满足的条件吗?
第2课时 二次根式的除法
(1)利用归纳类比的方法得出二次根式的除法法则和商的算术平方根的性质;
(2)会进行简单的二次根式的除法运算;
?(3) 理解最简二次根式的概念.
教学目标
复习提问,探究规律
二次根式的乘法法则是什么内容?化简二次根式的一般步骤怎样?
知识 1
二次根式除法的运算法则
2
3
=
=
=
=
思考 通过上述二次根式除法运算结果,联想到二次根式除法运算法则,你能说出二次根式 的结果吗?
两个二次根式相除,把被开方数相除,根指
数不变,即: (a≥0,b>0).
二次根式的除法法则:
文字叙述:
算术平方根的商等于被开方数商的算术平方根.
当二次根式根号外的因数(式)不为1时,可类比单项式除以单项式法则,易得
对比乘法法则里字母的取值范围,除法法则里字母的取值范围有何变化?
例1 计算:
解:
小结
利用二次根式的除法法则进行计算,被开方
数相除时,可以用“除以一个不为零的数等于乘这
个数的倒数”进行约分、化简.
1.计算
你有几种方法去掉分母中的根号?去分母的依据分别是什么? 再提问:第(2)题用什么方法计算更简捷?第(3)题根号下含字母在移出根号时应注意什么?
2.计算 的结果是__________.
3. 计算 的结果是( )
A. B. C. D.
知识 2
二次根式除法法则的逆运用
把 反过来,就得到
利用它可以进行二次根式的化简
二次根式的商的算术平方根的性质:
例2 化简:
解:
二次根式的运算结果有以下特点:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
知识 3
最简二次根式
简记为:一根号无分母,分母无根号;二不能再开方.
在二次根式的运算中,一般要把最后结果化为最简二次根式,并且分母中不含二次根式.
下列二次根式是否是最简二次根式?为什么?
例3
例4 设长方形的面积为S,相邻两边长分别为a,b.已知 ,求a的值.
学生独立思考写出答案,组内交流,小组展示
随堂检测
1 把下列二次根式化成最简二次根式:
(1) (2)
2.下列各式中,是最简二次根式的是( )
3.若使等式 成立,则实数k取值范围是 ( )
A.k≥1 B.k≥2
C. 1<k≤2 D. 1≤k≤2
4.已知xy<0,化简二次根式 的正确结果为( )
A. B.
C. D.
6.化简
归纳小结
共同回顾本节课所学内容,回答以下问题: (1)除法运算的法则如何?对等式中字母的取值范围有何要求? (2)你能说明最简二次根式需要满足的条件吗?
