人教版八年级上册11.2.1三角形的内角(第一课时)课件(共33张ppt)
文档属性
| 名称 | 人教版八年级上册11.2.1三角形的内角(第一课时)课件(共33张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 572.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 20:55:03 | ||
图片预览





文档简介
三角形的内角(第一课时)
课前准备
三角形纸片,剪刀,量角器,直尺.
在小学我们已经知道任意一个三角形的三个内角的和等于180°,你还记得是怎么发现这个结论的吗?
请大家利用手中的三角形纸片进行探究.
量一量、剪一剪、拼一拼:
方法 用量角器测量三角形的三个内角的度数,
并相加.
测量有误差,有些同学测量的三角形的三个内角的和不是180°.
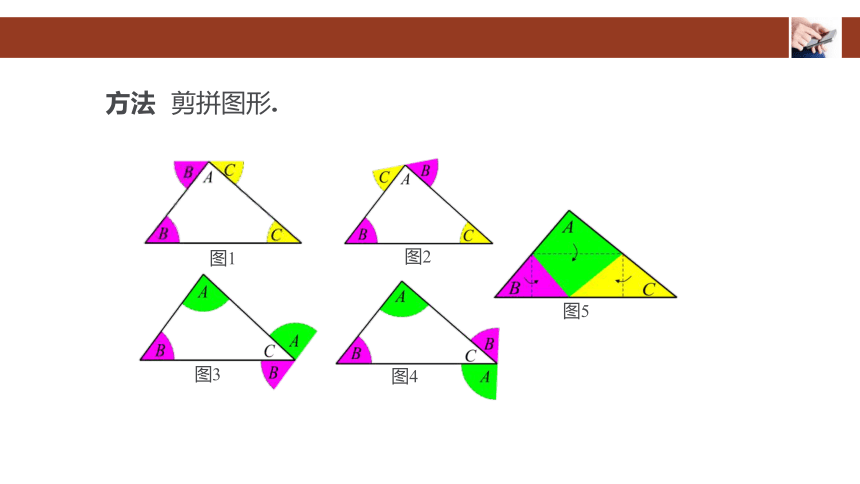
方法 剪拼图形.
图1
图2
图3
图4
图5
这些“验证” 不是“数学证明”
需要通过推理的方法来证明:
任意一个三角形的三个内角的和等于180°.
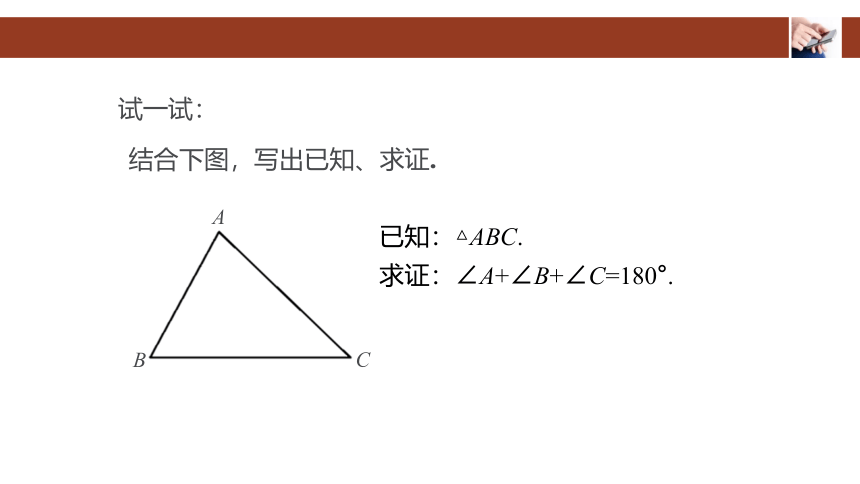
结合下图,写出已知、求证.
已知:△ABC.
求证:∠A+∠B+∠C=180°.
试一试:
A
B
C
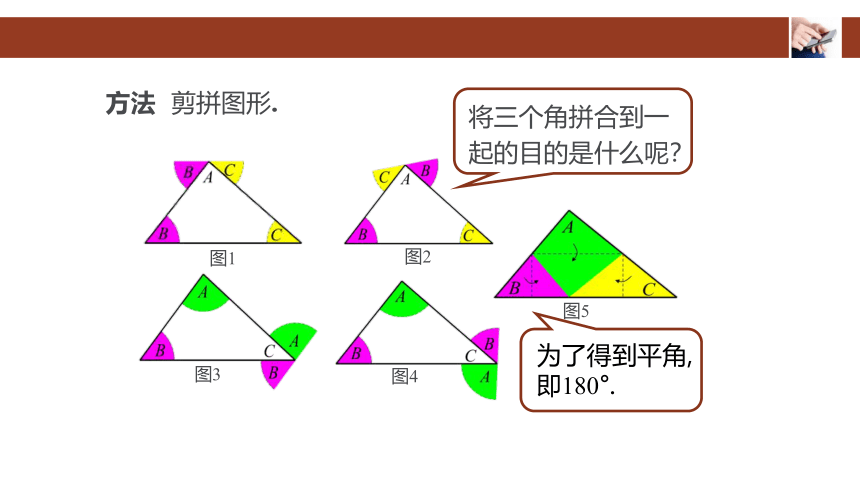
方法 剪拼图形.
图1
图2
图3
图4
图5
将三个角拼合到一起的目的是什么呢?
为了得到平角,
即180°.
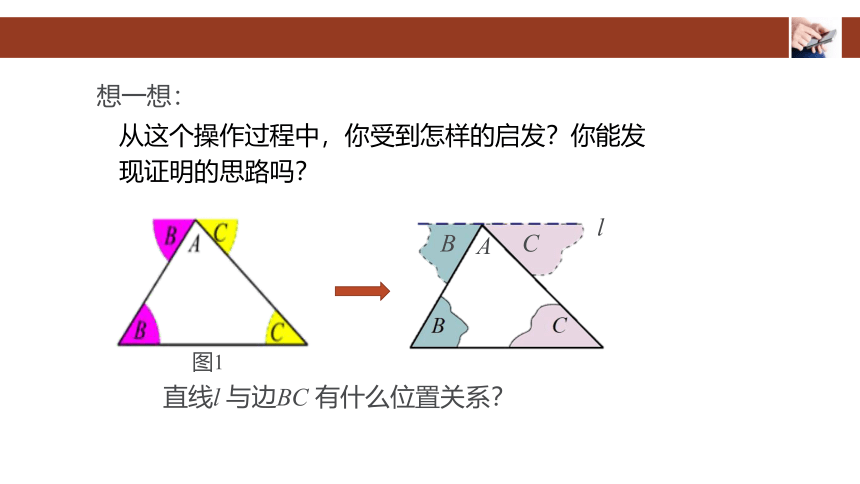
从这个操作过程中,你受到怎样的启发?你能发现证明的思路吗?
直线l 与边BC 有什么位置关系?
想一想:
B
C
A
l
图1
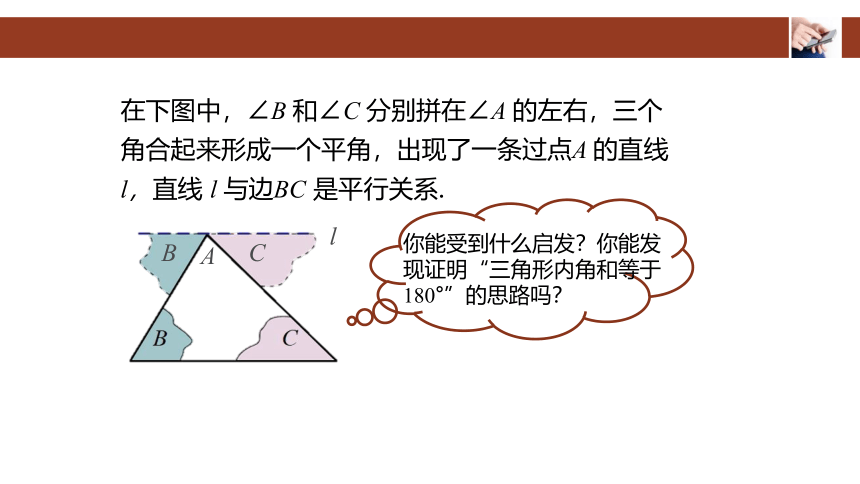
在下图中,∠B 和∠C 分别拼在∠A 的左右,三个角合起来形成一个平角,出现了一条过点A 的直线 l,直线 l 与边BC 是平行关系.
B
C
A
l
你能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
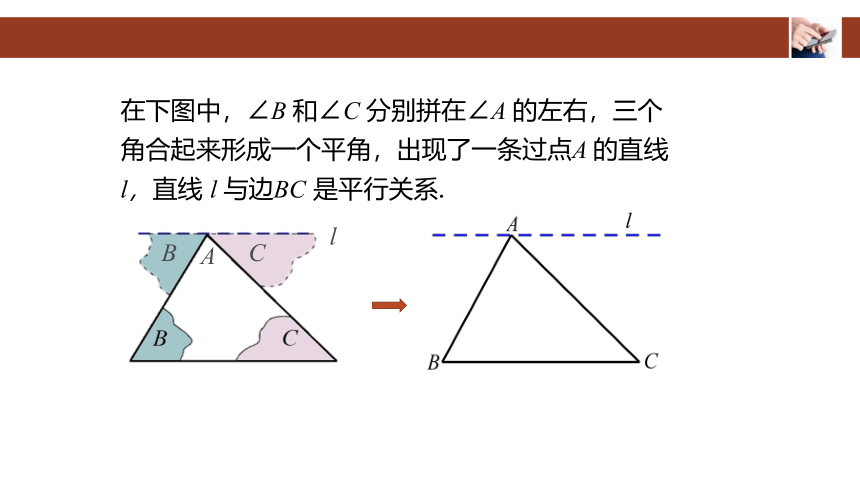
在下图中,∠B 和∠C 分别拼在∠A 的左右,三个角合起来形成一个平角,出现了一条过点A 的直线 l,直线 l 与边BC 是平行关系.
B
C
A
l
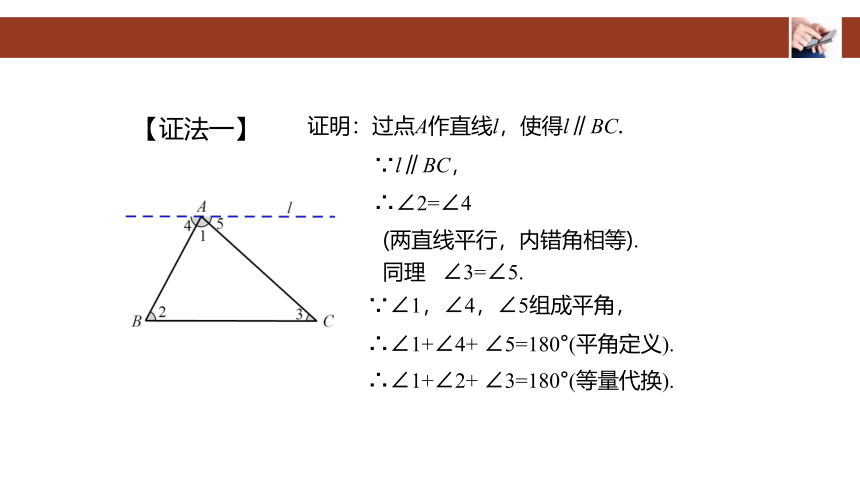
证明:过点A作直线l,使得l∥BC.
∵l∥BC,
∴∠2=∠4
(两直线平行,内错角相等).
同理 ∠3=∠5.
∵∠1,∠4,∠5组成平角,∴∠1+∠4+ ∠5=180°(平角定义).
∴∠1+∠2+ ∠3=180°(等量代换).
【证法一】
在△ABC中,
∠A+∠B+∠C=180°.
三角形内角和定理
三角形三个内角的和等于180°.
将剪下的两个角拼在了第三个角的同一侧,这样也能形成一个平角,也就是下图的形式.
你能模仿前面的证明过 程,用这名同学提供的方法证明此定理吗?
结合图形,写出证明.
证明:延长BC,过点C作直线l,使得l∥AB.
∵l∥BC,
∴∠1=∠4(两直线平行,内错角相等).
∠2=∠5(两直线平行,同位角相等).
∴∠1+∠2+ ∠3=180°(等量代换).
∵∠3,∠4,∠5组成平角,
∴∠3+∠4+ ∠5=180°(平角定义).
【证法二】
通过前面的操作和证明过程,你能受到什么启发?你能用其他方法证明此定理吗?
利用平行线的性质转移角,利用平角的定义得到180°.
在三角形的边上任取一点P,分别作两边的平行线.
在三角形的内部或外部任取一点,分别作三边的平行线,将三角形的三个内角转化为一个平角.
图1
图2
图3
图4
图5
两直线平行,同旁内角互补.
平角 180°
【证法三】
证明:过点C作CD∥AB,
则∠4=∠1(两直线平行,内错角相等),
∠2+∠BCD=180°
(两直线平行,同旁内角互补).
即∠2+∠3+∠4=180°.
∴∠2+∠3+∠1=180°(等量代换).
证明:过点B任意作一条直线BD,分别 过
点A、C作BD的平行线AE、CF.
∴∠ABC +∠ACB+∠BAC =180°.
则CF∥AE∥BD,
∴∠1=∠2,∠3=∠4,
∠DBC +∠BCF=180°.
即∠1+∠ABC +∠ACB +∠4=180°.
【证法四】
得到180°的方法:
平角定义;两直线平行,同旁内角互补.
练习 求出下列图形中的x的值:
练一练:
x°+39°+ 108°=180°
x°=180°-39°-108°=33°
x°=180°-60°-80°=40°
(1)
(2)
练习 求出下列图形中的x的值:
练一练:
x°=180°-105°-30°=45°
在一个三角形中,已知两个角的度数,就可以利用三角形内角和定理,求出第三个角的度数.
(3)
例 如图,在△ABC 中, ∠BAC =40°, ∠B = 75°,
AD 是△ABC 的角平分线.求∠ADB 的度数.
分析:∠ADB 是△ABD 的一个内角,在
△ABD 中,∠B = 75°,如果能得到
∠BAD的度数,就能求出∠ADB 的度
数.由∠BAC =40°,AD 是△ABC 的
角平分线,很容易得到∠BAD=20°.
例 如图,在△ABC 中, ∠BAC =40°, ∠B = 75°,
AD 是△ABC 的角平分线.求∠ADB 的度数.
解:由∠BAC=40°, AD是△ ABC的角
平分线,得
∠BAD= ∠BAC=20°.
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°=85°.
练习 如图,一种滑翔伞的形状是左右对称的四边
形ABCD,其中∠A=150°, ∠B=∠D=40°,
求∠C的度数.
提示:由四边形ABCD左右对称得
∠BAC=∠DAC=75°.
由∠ACB=180°-∠BAC-∠B,
求出∠ACB的度数.
课堂小结
2、为什么要用推理的方法证明“三角形的内角和等于180°”?
1、本节课学习了哪些主要内容?
3、你是怎么找到三角形内角和定理的证明思路的?
泰勒斯拼图验证
毕达哥拉斯的证法
欧几里得的证法
普罗克拉斯方案
教科书 第16页 习题11.2
作 业
1. 求出下列图形中的x的值:
(1)
(2)
(3)
(4)
3.△ABC中,∠B=∠A+10°,∠C=∠B+10°.
求△ABC的各内角的度数.
同学们,再见!
课前准备
三角形纸片,剪刀,量角器,直尺.
在小学我们已经知道任意一个三角形的三个内角的和等于180°,你还记得是怎么发现这个结论的吗?
请大家利用手中的三角形纸片进行探究.
量一量、剪一剪、拼一拼:
方法 用量角器测量三角形的三个内角的度数,
并相加.
测量有误差,有些同学测量的三角形的三个内角的和不是180°.
方法 剪拼图形.
图1
图2
图3
图4
图5
这些“验证” 不是“数学证明”
需要通过推理的方法来证明:
任意一个三角形的三个内角的和等于180°.
结合下图,写出已知、求证.
已知:△ABC.
求证:∠A+∠B+∠C=180°.
试一试:
A
B
C
方法 剪拼图形.
图1
图2
图3
图4
图5
将三个角拼合到一起的目的是什么呢?
为了得到平角,
即180°.
从这个操作过程中,你受到怎样的启发?你能发现证明的思路吗?
直线l 与边BC 有什么位置关系?
想一想:
B
C
A
l
图1
在下图中,∠B 和∠C 分别拼在∠A 的左右,三个角合起来形成一个平角,出现了一条过点A 的直线 l,直线 l 与边BC 是平行关系.
B
C
A
l
你能受到什么启发?你能发现证明“三角形内角和等于180°”的思路吗?
在下图中,∠B 和∠C 分别拼在∠A 的左右,三个角合起来形成一个平角,出现了一条过点A 的直线 l,直线 l 与边BC 是平行关系.
B
C
A
l
证明:过点A作直线l,使得l∥BC.
∵l∥BC,
∴∠2=∠4
(两直线平行,内错角相等).
同理 ∠3=∠5.
∵∠1,∠4,∠5组成平角,∴∠1+∠4+ ∠5=180°(平角定义).
∴∠1+∠2+ ∠3=180°(等量代换).
【证法一】
在△ABC中,
∠A+∠B+∠C=180°.
三角形内角和定理
三角形三个内角的和等于180°.
将剪下的两个角拼在了第三个角的同一侧,这样也能形成一个平角,也就是下图的形式.
你能模仿前面的证明过 程,用这名同学提供的方法证明此定理吗?
结合图形,写出证明.
证明:延长BC,过点C作直线l,使得l∥AB.
∵l∥BC,
∴∠1=∠4(两直线平行,内错角相等).
∠2=∠5(两直线平行,同位角相等).
∴∠1+∠2+ ∠3=180°(等量代换).
∵∠3,∠4,∠5组成平角,
∴∠3+∠4+ ∠5=180°(平角定义).
【证法二】
通过前面的操作和证明过程,你能受到什么启发?你能用其他方法证明此定理吗?
利用平行线的性质转移角,利用平角的定义得到180°.
在三角形的边上任取一点P,分别作两边的平行线.
在三角形的内部或外部任取一点,分别作三边的平行线,将三角形的三个内角转化为一个平角.
图1
图2
图3
图4
图5
两直线平行,同旁内角互补.
平角 180°
【证法三】
证明:过点C作CD∥AB,
则∠4=∠1(两直线平行,内错角相等),
∠2+∠BCD=180°
(两直线平行,同旁内角互补).
即∠2+∠3+∠4=180°.
∴∠2+∠3+∠1=180°(等量代换).
证明:过点B任意作一条直线BD,分别 过
点A、C作BD的平行线AE、CF.
∴∠ABC +∠ACB+∠BAC =180°.
则CF∥AE∥BD,
∴∠1=∠2,∠3=∠4,
∠DBC +∠BCF=180°.
即∠1+∠ABC +∠ACB +∠4=180°.
【证法四】
得到180°的方法:
平角定义;两直线平行,同旁内角互补.
练习 求出下列图形中的x的值:
练一练:
x°+39°+ 108°=180°
x°=180°-39°-108°=33°
x°=180°-60°-80°=40°
(1)
(2)
练习 求出下列图形中的x的值:
练一练:
x°=180°-105°-30°=45°
在一个三角形中,已知两个角的度数,就可以利用三角形内角和定理,求出第三个角的度数.
(3)
例 如图,在△ABC 中, ∠BAC =40°, ∠B = 75°,
AD 是△ABC 的角平分线.求∠ADB 的度数.
分析:∠ADB 是△ABD 的一个内角,在
△ABD 中,∠B = 75°,如果能得到
∠BAD的度数,就能求出∠ADB 的度
数.由∠BAC =40°,AD 是△ABC 的
角平分线,很容易得到∠BAD=20°.
例 如图,在△ABC 中, ∠BAC =40°, ∠B = 75°,
AD 是△ABC 的角平分线.求∠ADB 的度数.
解:由∠BAC=40°, AD是△ ABC的角
平分线,得
∠BAD= ∠BAC=20°.
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°=85°.
练习 如图,一种滑翔伞的形状是左右对称的四边
形ABCD,其中∠A=150°, ∠B=∠D=40°,
求∠C的度数.
提示:由四边形ABCD左右对称得
∠BAC=∠DAC=75°.
由∠ACB=180°-∠BAC-∠B,
求出∠ACB的度数.
课堂小结
2、为什么要用推理的方法证明“三角形的内角和等于180°”?
1、本节课学习了哪些主要内容?
3、你是怎么找到三角形内角和定理的证明思路的?
泰勒斯拼图验证
毕达哥拉斯的证法
欧几里得的证法
普罗克拉斯方案
教科书 第16页 习题11.2
作 业
1. 求出下列图形中的x的值:
(1)
(2)
(3)
(4)
3.△ABC中,∠B=∠A+10°,∠C=∠B+10°.
求△ABC的各内角的度数.
同学们,再见!
