人教版八年级上册11.3.1多边形课件(共25张ppt)
文档属性
| 名称 | 人教版八年级上册11.3.1多边形课件(共25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 833.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 20:55:12 | ||
图片预览




文档简介
多边形
首先请同学们观察这几幅生活中的图片,你能从中抽象出几个由一些线段围成的图形吗?
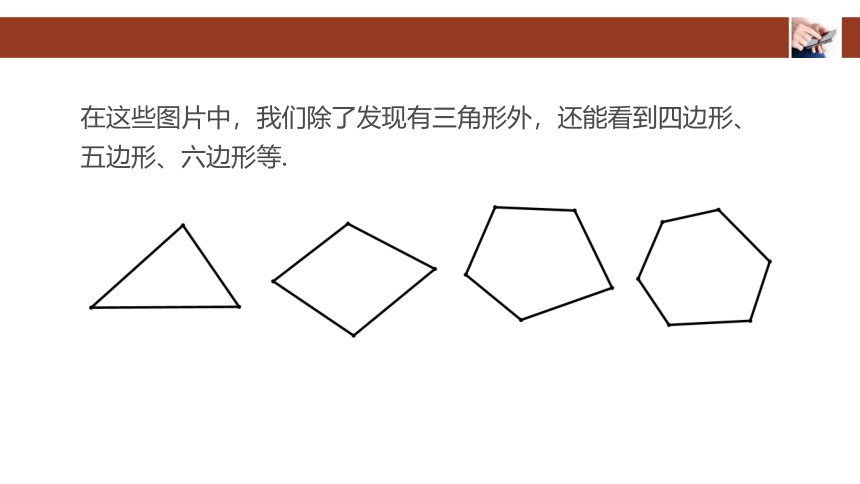
在这些图片中,我们除了发现有三角形外,还能看到四边形、五边形、六边形等.
请同学们回忆一下三角形的定义,什么是三角形呢?
由不在同一条直线上的三条线段首尾顺次相接
所组成的图形叫做三角形.
如图,△ABC,其中线段AB,BC,CA是三角形的边,
点A,B,C是三角形的顶点,∠A,∠B,∠C是三角形的角.
想一想,这些图形从构成看有什么共同特点?类比三角形的定义,你能得出什么叫四边形、五边形、多边形吗?
在平面内,由四条线段首尾顺次相接组成的图形叫做四边形;
由五条线段首尾顺次相接组成的图形叫做五边形.
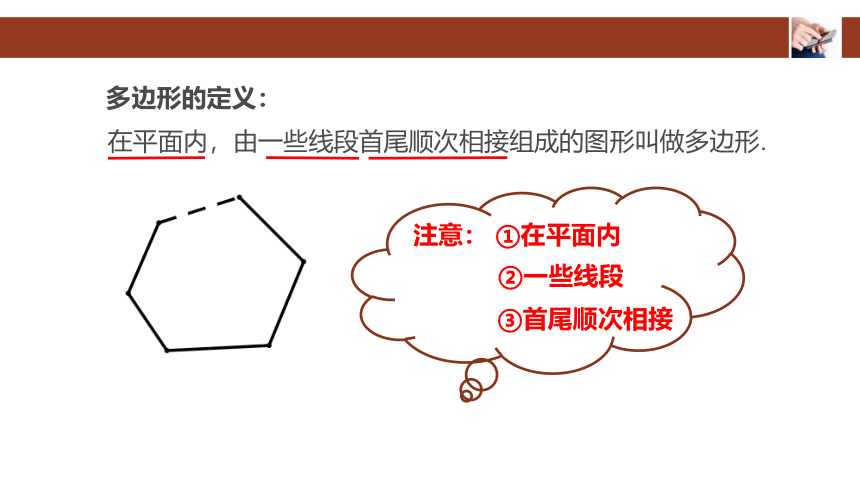
多边形的定义:
注意: ①在平面内
在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.
②一些线段
③首尾顺次相接
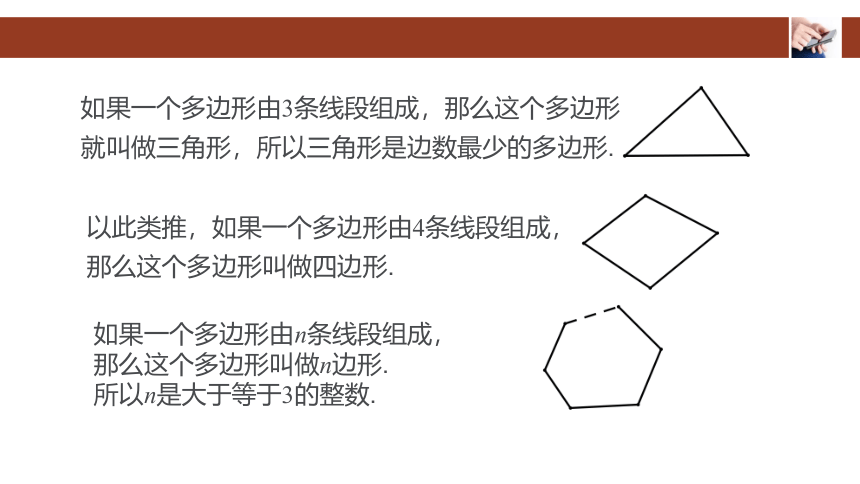
如果一个多边形由3条线段组成,那么这个多边形
就叫做三角形,所以三角形是边数最少的多边形.
以此类推,如果一个多边形由4条线段组成,
那么这个多边形叫做四边形.
如果一个多边形由n条线段组成,
那么这个多边形叫做n边形.
所以n是大于等于3的整数.
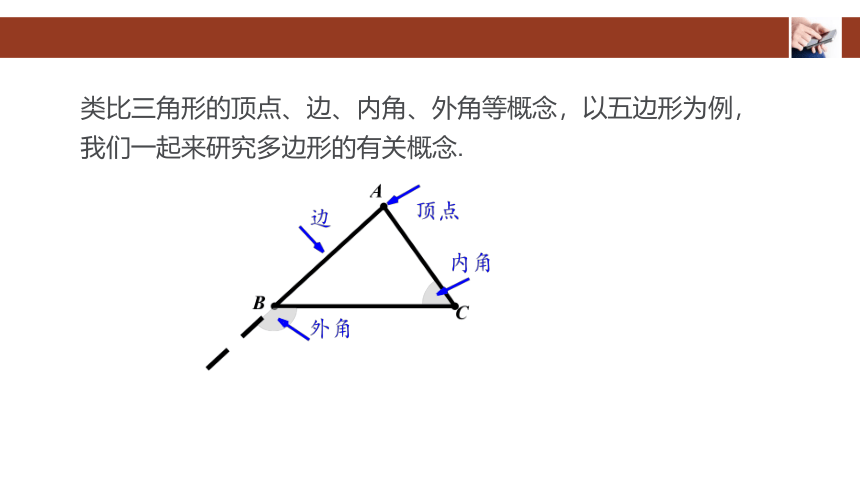
类比三角形的顶点、边、内角、外角等概念,以五边形为例,我们一起来研究多边形的有关概念.
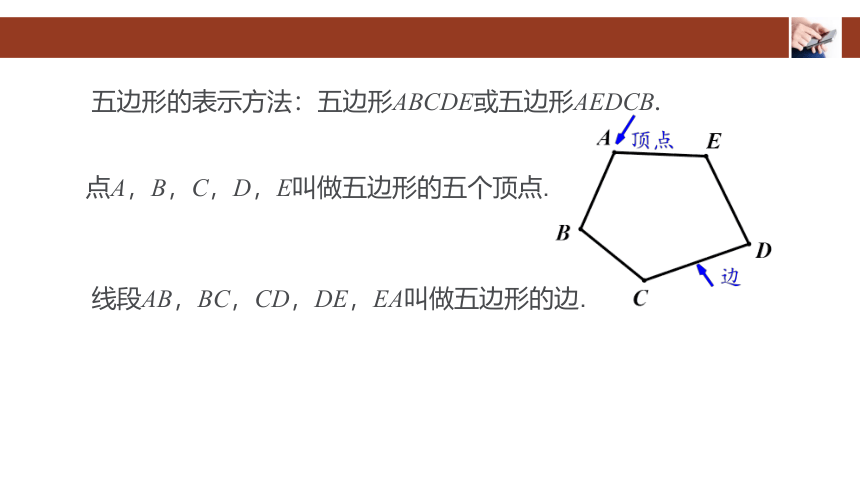
五边形的表示方法:五边形ABCDE或五边形AEDCB.
点A,B,C,D,E叫做五边形的五个顶点.
线段AB,BC,CD,DE,EA叫做五边形的边.
多边形相邻两边组成的角叫做它的内角,∠C,∠D等叫做
五边形的内角.
多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
所以∠1,∠2等都是五边形的外角.
n 边形有 n个顶点, n条边,
n 个内角,2 n 个外角.
连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
如图所示的线段AD,BE等都是五边形的对角线.
请同学们观察以下两幅图片有什么不同?
如图1,画出四边形ABCD的任何一条边所在直线,
如果整个四边形都在这条直线的同一侧,这样的四
边形叫做凸四边形.
如图2中的四边形ABCD 就不是凸四边形,因为画出边CD所在的直线,整个四边形不都在这条直线的同一侧.
本节只讨论凸多边形.
类似地,画出多边形的任何一条边所在直线,如果
整个多边形都在这条直线的同一侧,这样的多边形
叫做凸多边形.
各个角都相等,各条边都相等的多边形叫做正多边形.
等边三角形
正方形
正五边形
正六边形
每条边都相等的多边形是正多边形吗?
每个角都相等的多边形是正多边形吗?
你能在下列图案中找到几种正多边形?
(1)四边形ABCD有 条对角线,
它们分别是 .
?
?
?
?
?
?
下面我们一起重点研究对角线:
(2)从五边形ABCDE同一个顶点
出发的对角线有几条?
(3)五边形ABCDE共有多少条对角线呢?
请画出它的其他对角线.
两
AC,BD
通过四边形与五边形的研究发现,对角线在多边形中
有着很重要的地位.下面我们通过一个表格,来研究
n边形的对角线.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
四边形
五边形
六边形
n边形
图形
从一个顶点出发能作的对角线条数
过一个顶点的对角线把多边形分成的三角形的个数
对角线的总条数
1
2
3
n-3
2
3
4
n-2
2
5
9
练习 如图:
(1)图中的多边形记作 ;
(3)画出顶点A处的两个外角.
(2)AB边的邻边有 ;
五边形AECDB
AE,BD
十边形有几条对角线?
一个多边形共有5条对角线,那么这个多边形的边数是( )
A.3 B.4 C.5 D.6
C
方法1:
方法2:
连接多边形的一个顶点与其他顶点的线段把这个多边形
分成了6个三角形,则原多边形是( )
A.5 B.6 C.7 D.8
D
若一个长方形截去一个角后,剩余的部分是几边形?
课堂小结
1.知识汇总:
(1)多边形的定义;
2.思想方法:类比、转化等数学思想.
(3)凸多边形;
(2)多边形的边、角(内角、外角)、对角线;
对角线的主要作用:分割成三角形,把多边形的问题转化为三角形的问题来解决;
(4)正多边形.
布置作业
必做作业:教科书P21 练习1,2;
1.画出下列多边形的全部对角线:
2.四边形的一条对角线将四边形分成几个三角形?从五边形
的一个顶点出发,可以画出几条对角线?它们将五边形分成几个三角形?
选做作业:请你用若干个正多边形设计一幅美丽的图案,
并与你的同伴交流.
同学们,再见!
首先请同学们观察这几幅生活中的图片,你能从中抽象出几个由一些线段围成的图形吗?
在这些图片中,我们除了发现有三角形外,还能看到四边形、五边形、六边形等.
请同学们回忆一下三角形的定义,什么是三角形呢?
由不在同一条直线上的三条线段首尾顺次相接
所组成的图形叫做三角形.
如图,△ABC,其中线段AB,BC,CA是三角形的边,
点A,B,C是三角形的顶点,∠A,∠B,∠C是三角形的角.
想一想,这些图形从构成看有什么共同特点?类比三角形的定义,你能得出什么叫四边形、五边形、多边形吗?
在平面内,由四条线段首尾顺次相接组成的图形叫做四边形;
由五条线段首尾顺次相接组成的图形叫做五边形.
多边形的定义:
注意: ①在平面内
在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.
②一些线段
③首尾顺次相接
如果一个多边形由3条线段组成,那么这个多边形
就叫做三角形,所以三角形是边数最少的多边形.
以此类推,如果一个多边形由4条线段组成,
那么这个多边形叫做四边形.
如果一个多边形由n条线段组成,
那么这个多边形叫做n边形.
所以n是大于等于3的整数.
类比三角形的顶点、边、内角、外角等概念,以五边形为例,我们一起来研究多边形的有关概念.
五边形的表示方法:五边形ABCDE或五边形AEDCB.
点A,B,C,D,E叫做五边形的五个顶点.
线段AB,BC,CD,DE,EA叫做五边形的边.
多边形相邻两边组成的角叫做它的内角,∠C,∠D等叫做
五边形的内角.
多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
所以∠1,∠2等都是五边形的外角.
n 边形有 n个顶点, n条边,
n 个内角,2 n 个外角.
连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
如图所示的线段AD,BE等都是五边形的对角线.
请同学们观察以下两幅图片有什么不同?
如图1,画出四边形ABCD的任何一条边所在直线,
如果整个四边形都在这条直线的同一侧,这样的四
边形叫做凸四边形.
如图2中的四边形ABCD 就不是凸四边形,因为画出边CD所在的直线,整个四边形不都在这条直线的同一侧.
本节只讨论凸多边形.
类似地,画出多边形的任何一条边所在直线,如果
整个多边形都在这条直线的同一侧,这样的多边形
叫做凸多边形.
各个角都相等,各条边都相等的多边形叫做正多边形.
等边三角形
正方形
正五边形
正六边形
每条边都相等的多边形是正多边形吗?
每个角都相等的多边形是正多边形吗?
你能在下列图案中找到几种正多边形?
(1)四边形ABCD有 条对角线,
它们分别是 .
?
?
?
?
?
?
下面我们一起重点研究对角线:
(2)从五边形ABCDE同一个顶点
出发的对角线有几条?
(3)五边形ABCDE共有多少条对角线呢?
请画出它的其他对角线.
两
AC,BD
通过四边形与五边形的研究发现,对角线在多边形中
有着很重要的地位.下面我们通过一个表格,来研究
n边形的对角线.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
四边形
五边形
六边形
n边形
图形
从一个顶点出发能作的对角线条数
过一个顶点的对角线把多边形分成的三角形的个数
对角线的总条数
1
2
3
n-3
2
3
4
n-2
2
5
9
练习 如图:
(1)图中的多边形记作 ;
(3)画出顶点A处的两个外角.
(2)AB边的邻边有 ;
五边形AECDB
AE,BD
十边形有几条对角线?
一个多边形共有5条对角线,那么这个多边形的边数是( )
A.3 B.4 C.5 D.6
C
方法1:
方法2:
连接多边形的一个顶点与其他顶点的线段把这个多边形
分成了6个三角形,则原多边形是( )
A.5 B.6 C.7 D.8
D
若一个长方形截去一个角后,剩余的部分是几边形?
课堂小结
1.知识汇总:
(1)多边形的定义;
2.思想方法:类比、转化等数学思想.
(3)凸多边形;
(2)多边形的边、角(内角、外角)、对角线;
对角线的主要作用:分割成三角形,把多边形的问题转化为三角形的问题来解决;
(4)正多边形.
布置作业
必做作业:教科书P21 练习1,2;
1.画出下列多边形的全部对角线:
2.四边形的一条对角线将四边形分成几个三角形?从五边形
的一个顶点出发,可以画出几条对角线?它们将五边形分成几个三角形?
选做作业:请你用若干个正多边形设计一幅美丽的图案,
并与你的同伴交流.
同学们,再见!
