人教版八年级上册12.1全等三角形课件(23张)
文档属性
| 名称 | 人教版八年级上册12.1全等三角形课件(23张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 20:58:39 | ||
图片预览







文档简介
全等三角形
课前准备
铅笔,白纸,剪刀,量角器,三角尺,直尺.
找一找下面图案中形状、大小相同的图形.
你能再举出一些类似的例子吗?
探究 把一块三角尺按在纸板上,画下图形,照图形裁下来的纸板和三角尺的形状、大小完全一样吗?
你是用什么方法来验证的?
可以看到,形状、大小相同的图形放在一起能够完全重合,
能够完全重合的两个图形叫做全等形.
我们的研究对象,已经“升级”为两个图形了.我们关注
的,是它们之间的一种特殊的关系,即全等关系.
生活中存在丰富的全等形,从哪种全等形开始研究呢?
三角形的内角,内角和定理;
三角形的外角,三角形的外角等于与它不相邻的两个内角的和.
三角形的边;
三角形内的重要线段;
能够完全重合的
两个三角形叫做
全等三角形.
我们已经学习了与三角形有关的知识
三角形
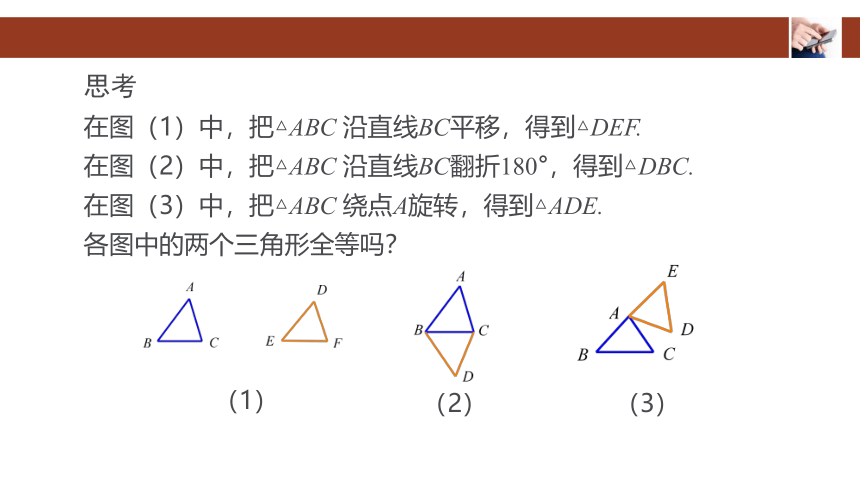
思考
在图(1)中,把△ABC 沿直线BC平移,得到△DEF.
在图(2)中,把△ABC 沿直线BC翻折180°,得到△DBC.
在图(3)中,把△ABC 绕点A旋转,得到△ADE.
各图中的两个三角形全等吗?
(1)
(2)
(3)
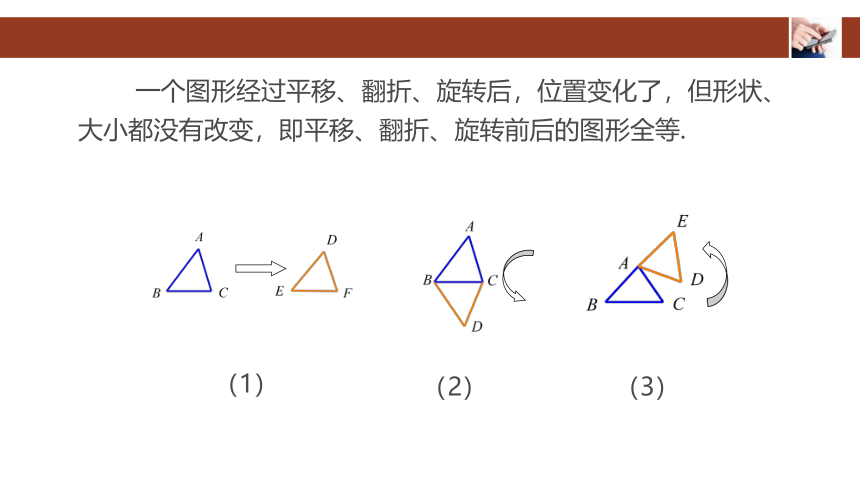
一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.
(1)
(2)
(3)
其中,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
(1)
点A和点D,点B和点E,点C和点F是
对应顶点;
AB和DE, BC和EF,AC和DF是对应边;
∠A和∠D,∠B和∠E,∠C和∠F是
对应角.
(1)
△ABC和△DEF全等,记做△ABC≌△DEF.
符号“≌”表示全等,读作“全等于”.
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
练习
同学们再试着在图(2)(3)中,找到对应顶点、对应边
和对应角,并写成△***≌△***的形式.
(2)
(3)
△ABC≌△DBC
△ABC≌△ADE
思考
图(1)中,△ABC≌△DEF,对应边有什么关系?对应角呢?
(1)
“完全重合”
全等三角形的对应边相等,全等三角形的对应角相等.
数学化
全等三角形的性质
∵△ABC≌△DEF,
∴ AB=DE, BC=EF, CA=FD,
∠A=∠D, ∠B=∠E, ∠C=∠F.
图
文
式
例 如图,△ABC≌△CDA,AB和CD,BC和DA是对应边,写出其他对应边及对应角.
其他对应边:AC与CA
对应角: ∠BAC与∠DCA,∠BCA与∠DAC,
∠B与∠D.
即使是同一条线段对应端点不同,结果也是不同的含义
(注意字母的顺序)
方法1 题目中有明确的符号表示,如△ABC≌△CDA,靠 字母排列的位置对应寻找;
方法2 如果题目中没有明确的符号表示,可以
从边的长短、角的大小出发.只有长度相同的边才
有可能成为对应边,大小相等的角,才有可能成为对应角;
方法3 从图形的生成过程出发,动态思考一个三角形是怎样与另一个三角形重合的.
练习 如图,△ABN≌△ACM,∠B和∠C是对应角,AB和AC是对应边.写出其他对应边及对应角.
对应边还有:AM与AN,BN与CM.
对应角还有:∠BAN与∠CAM,∠AMC与∠ANB.
例 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1等于多少度?
∠1=66°
利用全等三角形的性质求解
例 如图,△EFG≌△NMH,∠F和∠M是对应角,
在△EFG中,FG是最长边,在△NMH中,MH是最长边. EF=2.1 cm,EH=1.1 cm,NH=3.3 cm.
(1) 写出其他对应边及对应角;
(2) 求线段NM及线段HG的长度.
条件上图
(1)剩余的对应角为:
∠E与∠N,∠EGF与∠NHM
对应边为:EF与MN,EG与NH
∵ △EFG≌△NMH, EF=2.1
∴ MN=EF=2.1.
(全等三角形的对应边相等)
∵△EFG≌△NMH,
HN=3.3,
∴GE=HN=3.3.
(全等三角形的对应边相等)
∵HG=GE-EH, EH=1.1,
∴HG=3.3-1.1=2.2.
(2)求线段HG的长度.
HG
EG-EH
HN
1.1
3.3
线段的运算
全等三角形的
对应边相等
1 研究对象
我们现在的研究对象已经不局限在一个图形里,而是扩充到研究两个图形(三角形)之间的关系.
3 研究应用
帮助我们推得对应线段、对应角之间的等量关系.
2 研究内容
全等,就是两个图形间,最为特殊且基本的关系之一.
作业
1. 如图,△ABC≌△DEC,CA和CD, CB和CE是对应边.
∠ACD和∠BCE相等吗?为什么?
2. 如图,△AEC≌△ADB,点E和点D是 对应顶点.
(1)写出它们的对应边和对应角;
(2)若∠A=50°,∠ABD=39°,
且∠1=∠2,求∠1的度数.
同学们,再见!
课前准备
铅笔,白纸,剪刀,量角器,三角尺,直尺.
找一找下面图案中形状、大小相同的图形.
你能再举出一些类似的例子吗?
探究 把一块三角尺按在纸板上,画下图形,照图形裁下来的纸板和三角尺的形状、大小完全一样吗?
你是用什么方法来验证的?
可以看到,形状、大小相同的图形放在一起能够完全重合,
能够完全重合的两个图形叫做全等形.
我们的研究对象,已经“升级”为两个图形了.我们关注
的,是它们之间的一种特殊的关系,即全等关系.
生活中存在丰富的全等形,从哪种全等形开始研究呢?
三角形的内角,内角和定理;
三角形的外角,三角形的外角等于与它不相邻的两个内角的和.
三角形的边;
三角形内的重要线段;
能够完全重合的
两个三角形叫做
全等三角形.
我们已经学习了与三角形有关的知识
三角形
思考
在图(1)中,把△ABC 沿直线BC平移,得到△DEF.
在图(2)中,把△ABC 沿直线BC翻折180°,得到△DBC.
在图(3)中,把△ABC 绕点A旋转,得到△ADE.
各图中的两个三角形全等吗?
(1)
(2)
(3)
一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.
(1)
(2)
(3)
其中,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
(1)
点A和点D,点B和点E,点C和点F是
对应顶点;
AB和DE, BC和EF,AC和DF是对应边;
∠A和∠D,∠B和∠E,∠C和∠F是
对应角.
(1)
△ABC和△DEF全等,记做△ABC≌△DEF.
符号“≌”表示全等,读作“全等于”.
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
练习
同学们再试着在图(2)(3)中,找到对应顶点、对应边
和对应角,并写成△***≌△***的形式.
(2)
(3)
△ABC≌△DBC
△ABC≌△ADE
思考
图(1)中,△ABC≌△DEF,对应边有什么关系?对应角呢?
(1)
“完全重合”
全等三角形的对应边相等,全等三角形的对应角相等.
数学化
全等三角形的性质
∵△ABC≌△DEF,
∴ AB=DE, BC=EF, CA=FD,
∠A=∠D, ∠B=∠E, ∠C=∠F.
图
文
式
例 如图,△ABC≌△CDA,AB和CD,BC和DA是对应边,写出其他对应边及对应角.
其他对应边:AC与CA
对应角: ∠BAC与∠DCA,∠BCA与∠DAC,
∠B与∠D.
即使是同一条线段对应端点不同,结果也是不同的含义
(注意字母的顺序)
方法1 题目中有明确的符号表示,如△ABC≌△CDA,靠 字母排列的位置对应寻找;
方法2 如果题目中没有明确的符号表示,可以
从边的长短、角的大小出发.只有长度相同的边才
有可能成为对应边,大小相等的角,才有可能成为对应角;
方法3 从图形的生成过程出发,动态思考一个三角形是怎样与另一个三角形重合的.
练习 如图,△ABN≌△ACM,∠B和∠C是对应角,AB和AC是对应边.写出其他对应边及对应角.
对应边还有:AM与AN,BN与CM.
对应角还有:∠BAN与∠CAM,∠AMC与∠ANB.
例 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1等于多少度?
∠1=66°
利用全等三角形的性质求解
例 如图,△EFG≌△NMH,∠F和∠M是对应角,
在△EFG中,FG是最长边,在△NMH中,MH是最长边. EF=2.1 cm,EH=1.1 cm,NH=3.3 cm.
(1) 写出其他对应边及对应角;
(2) 求线段NM及线段HG的长度.
条件上图
(1)剩余的对应角为:
∠E与∠N,∠EGF与∠NHM
对应边为:EF与MN,EG与NH
∵ △EFG≌△NMH, EF=2.1
∴ MN=EF=2.1.
(全等三角形的对应边相等)
∵△EFG≌△NMH,
HN=3.3,
∴GE=HN=3.3.
(全等三角形的对应边相等)
∵HG=GE-EH, EH=1.1,
∴HG=3.3-1.1=2.2.
(2)求线段HG的长度.
HG
EG-EH
HN
1.1
3.3
线段的运算
全等三角形的
对应边相等
1 研究对象
我们现在的研究对象已经不局限在一个图形里,而是扩充到研究两个图形(三角形)之间的关系.
3 研究应用
帮助我们推得对应线段、对应角之间的等量关系.
2 研究内容
全等,就是两个图形间,最为特殊且基本的关系之一.
作业
1. 如图,△ABC≌△DEC,CA和CD, CB和CE是对应边.
∠ACD和∠BCE相等吗?为什么?
2. 如图,△AEC≌△ADB,点E和点D是 对应顶点.
(1)写出它们的对应边和对应角;
(2)若∠A=50°,∠ABD=39°,
且∠1=∠2,求∠1的度数.
同学们,再见!
