人教版八年级上册12.2全等三角形的性质与判定的综合运用(第二课时)课件(20张)
文档属性
| 名称 | 人教版八年级上册12.2全等三角形的性质与判定的综合运用(第二课时)课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 237.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览






文档简介
全等三角形的性质与判定的综合运用
(第二课时)
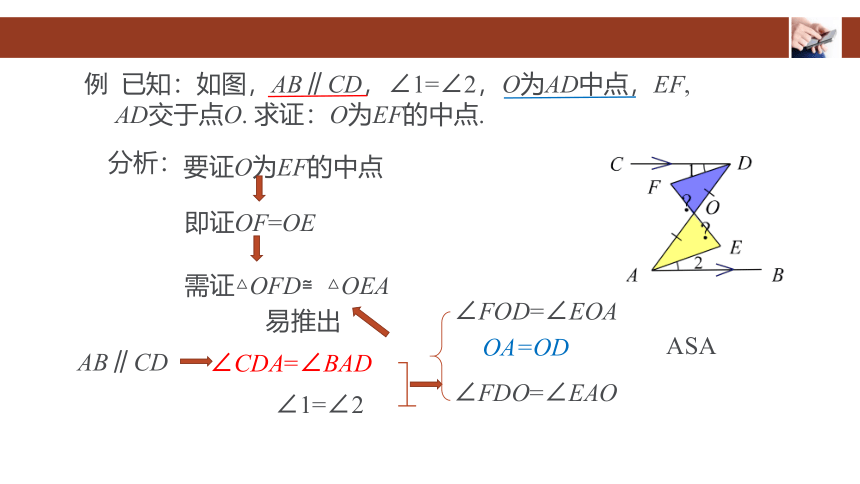
例 已知:如图,AB∥CD,∠1=∠2,O为AD中点,EF,
AD交于点O. 求证:O为EF的中点.
例 已知:如图,AB∥CD,∠1=∠2,O为AD中点,EF,
AD交于点O. 求证:O为EF的中点.
分析:
要证O为EF的中点
即证OF=OE
需证△OFD≌△OEA
AB∥CD
OA=OD
∠FOD=∠EOA
∠1=∠2
∠FDO=∠EAO
∠CDA=∠BAD
ASA
易推出
证明:
∵AB∥CD,
∴∠CDA=∠BAD.
又∵∠1=∠2,
∴∠CDA-∠1=∠BAD - ∠2.
即∠FDO=∠EAO.
∵O为AD的中点,
∴OA=OD.
在△OFD和△OEA中,
∴△OFD≌△OEA(ASA).
∴OF=OE.
∴ O是EF的中点.
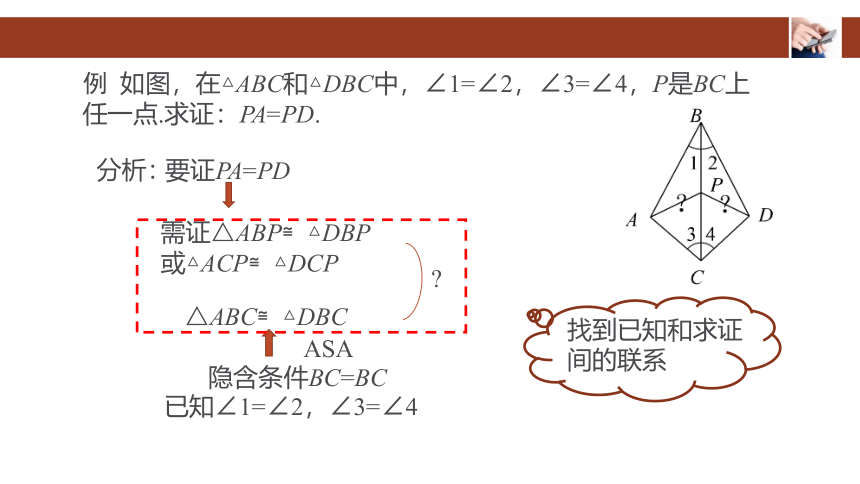
例 如图,在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是
BC上任一点.求证:PA=PD.
例 如图,在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是BC上任一点.求证:PA=PD.
要证PA=PD
分析:
需证△ABP≌△DBP
或△ACP≌△DCP
已知∠1=∠2,∠3=∠4
隐含条件BC=BC
ASA
△ABC≌△DBC
找到已知和求证
间的联系
?
证明:
在△ABC和△DBC中,
在△ABP和△DBP中,
∴△ABC≌△DBC(ASA) .
∴AB=DB.
∴△ABP≌△DBP(SAS).
∴PA=PD.
(全等三角形的对应边相等 )
第一次全等为第二次全等提供了条件
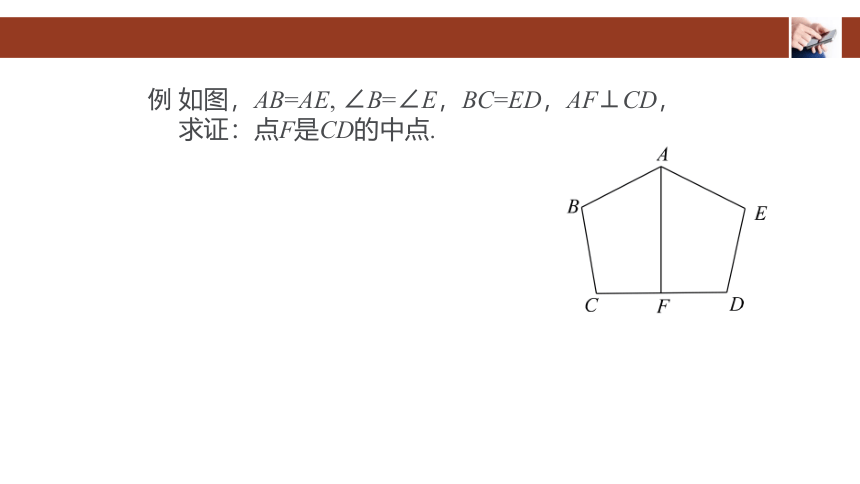
例 如图,AB=AE, ∠B=∠E,BC=ED,AF⊥CD,
求证:点F是CD的中点.
要证F是CD的中点
分析:
即证CF=DF
需证△ACF≌△ADF
已知AB=AE, ∠B=∠E,BC=ED
SAS
△ABC≌△AED
AC=AD
AF⊥CD
AF=AF
HL
证明:连接AC、AD.
在△ABC和△AED中,
∴△ABC≌△AED(SAS).
∴AC=AD.
∵AF⊥CD .
∴∠AFC=∠AFD=90°.
在Rt△AFC和Rt△AFD中,
∴Rt△AFC≌Rt△AFD(HL).
∴CF=DF.
∴点F是CD的中点.
例 如图,点A ,B ,C ,D在一条直线上,且AB=CD,
若∠1=∠2,EC=FB.求证:∠E=∠F.
要证∠E=∠F.
分析:
需证△ACF≌△ADF
已知AB=CD
AB+BC=CD+BC
AC=BD
已知∠1=∠2
∠ABC=∠BCD=180°
∠ABC-∠1=∠BCD-∠2
∠DBF=∠ACE
SAS
证明:
∵AB=CD,
∴AB+BC=CD+BC. 即AC=BD.
∵∠ABC=∠BCD=180°,
∠1=∠2 ,
∴∠ABC-∠1=∠BCD-∠2.
即∠DBF=∠ACE.
在△AEC和△DFB中,
∴△AEC≌DFB (SAS).
∴∠E=∠F.
练习 如图,点B, F, C, E在一条直线上,FB=CE,AB∥ED,
AC∥FD. 求证:AB=DE, AC=DF.
证明:
∵FB=CE,
∴FB+FC=CE+FC.
即BC=EF.
∵AB∥ED,
∴∠B=∠E.
∵AC∥FD,
∴∠ACB=∠DFE.
在△ABC和△DEF中,
∴△ABC≌△DEF (ASA).
∴AB=DE , AC=DF.
课堂小结
证明题的分析思路:
①要证什么
②已有什么
③还缺什么
④推导条件
课堂小结
全等三角形,是证明两条线段或两个角相等的重要方法
之一,证明时:
①要观察待证的线段或角,在哪两个可能全等的三角形中;
②有公共边,公共边一定是对应边,有公共角的,公共角
一定是对应角,有对顶角,对顶角也是对应角.
证明的书写步骤:
①准备条件:证全等时要用的条件要先证好;
②三角形全等书写三步骤:
写出在哪两个三角形中,
摆出三个条件用大括号括起来,
写出全等结论.
课堂小结
课后作业
如图,AC,BD交与点O, AC=BD, AB=CD.
求证:(1)∠C=∠B (2)OA=OD.
2. 如图, AB=AC, AE=AD, ∠1= ∠2.
求证: BD=CE.
同学们,再见!
(第二课时)
例 已知:如图,AB∥CD,∠1=∠2,O为AD中点,EF,
AD交于点O. 求证:O为EF的中点.
例 已知:如图,AB∥CD,∠1=∠2,O为AD中点,EF,
AD交于点O. 求证:O为EF的中点.
分析:
要证O为EF的中点
即证OF=OE
需证△OFD≌△OEA
AB∥CD
OA=OD
∠FOD=∠EOA
∠1=∠2
∠FDO=∠EAO
∠CDA=∠BAD
ASA
易推出
证明:
∵AB∥CD,
∴∠CDA=∠BAD.
又∵∠1=∠2,
∴∠CDA-∠1=∠BAD - ∠2.
即∠FDO=∠EAO.
∵O为AD的中点,
∴OA=OD.
在△OFD和△OEA中,
∴△OFD≌△OEA(ASA).
∴OF=OE.
∴ O是EF的中点.
例 如图,在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是
BC上任一点.求证:PA=PD.
例 如图,在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是BC上任一点.求证:PA=PD.
要证PA=PD
分析:
需证△ABP≌△DBP
或△ACP≌△DCP
已知∠1=∠2,∠3=∠4
隐含条件BC=BC
ASA
△ABC≌△DBC
找到已知和求证
间的联系
?
证明:
在△ABC和△DBC中,
在△ABP和△DBP中,
∴△ABC≌△DBC(ASA) .
∴AB=DB.
∴△ABP≌△DBP(SAS).
∴PA=PD.
(全等三角形的对应边相等 )
第一次全等为第二次全等提供了条件
例 如图,AB=AE, ∠B=∠E,BC=ED,AF⊥CD,
求证:点F是CD的中点.
要证F是CD的中点
分析:
即证CF=DF
需证△ACF≌△ADF
已知AB=AE, ∠B=∠E,BC=ED
SAS
△ABC≌△AED
AC=AD
AF⊥CD
AF=AF
HL
证明:连接AC、AD.
在△ABC和△AED中,
∴△ABC≌△AED(SAS).
∴AC=AD.
∵AF⊥CD .
∴∠AFC=∠AFD=90°.
在Rt△AFC和Rt△AFD中,
∴Rt△AFC≌Rt△AFD(HL).
∴CF=DF.
∴点F是CD的中点.
例 如图,点A ,B ,C ,D在一条直线上,且AB=CD,
若∠1=∠2,EC=FB.求证:∠E=∠F.
要证∠E=∠F.
分析:
需证△ACF≌△ADF
已知AB=CD
AB+BC=CD+BC
AC=BD
已知∠1=∠2
∠ABC=∠BCD=180°
∠ABC-∠1=∠BCD-∠2
∠DBF=∠ACE
SAS
证明:
∵AB=CD,
∴AB+BC=CD+BC. 即AC=BD.
∵∠ABC=∠BCD=180°,
∠1=∠2 ,
∴∠ABC-∠1=∠BCD-∠2.
即∠DBF=∠ACE.
在△AEC和△DFB中,
∴△AEC≌DFB (SAS).
∴∠E=∠F.
练习 如图,点B, F, C, E在一条直线上,FB=CE,AB∥ED,
AC∥FD. 求证:AB=DE, AC=DF.
证明:
∵FB=CE,
∴FB+FC=CE+FC.
即BC=EF.
∵AB∥ED,
∴∠B=∠E.
∵AC∥FD,
∴∠ACB=∠DFE.
在△ABC和△DEF中,
∴△ABC≌△DEF (ASA).
∴AB=DE , AC=DF.
课堂小结
证明题的分析思路:
①要证什么
②已有什么
③还缺什么
④推导条件
课堂小结
全等三角形,是证明两条线段或两个角相等的重要方法
之一,证明时:
①要观察待证的线段或角,在哪两个可能全等的三角形中;
②有公共边,公共边一定是对应边,有公共角的,公共角
一定是对应角,有对顶角,对顶角也是对应角.
证明的书写步骤:
①准备条件:证全等时要用的条件要先证好;
②三角形全等书写三步骤:
写出在哪两个三角形中,
摆出三个条件用大括号括起来,
写出全等结论.
课堂小结
课后作业
如图,AC,BD交与点O, AC=BD, AB=CD.
求证:(1)∠C=∠B (2)OA=OD.
2. 如图, AB=AC, AE=AD, ∠1= ∠2.
求证: BD=CE.
同学们,再见!
