人教版八年级上册12.2全等三角形的性质与判定的综合运用(第三课时)课件(24张)
文档属性
| 名称 | 人教版八年级上册12.2全等三角形的性质与判定的综合运用(第三课时)课件(24张) |  | |
| 格式 | pptx | ||
| 文件大小 | 272.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:00:21 | ||
图片预览




文档简介
全等三角形的性质与判定的综合运用
(第三课时)
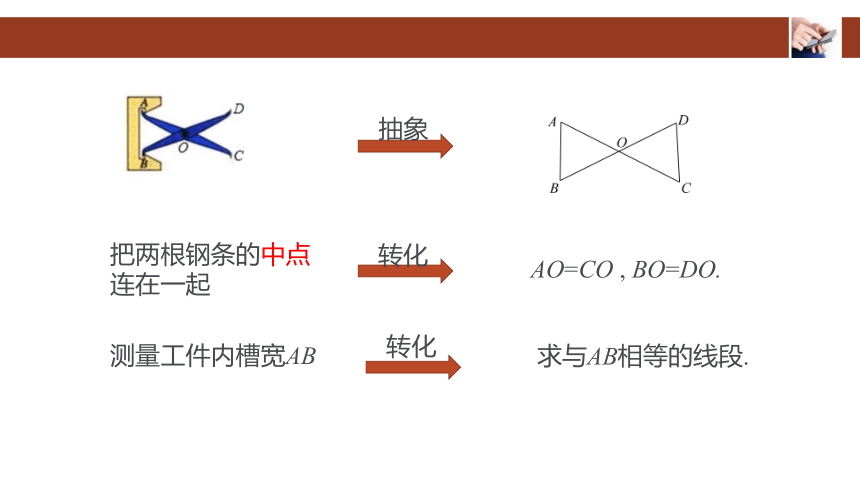
例 如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳). 在图中,要测量工件内槽宽AB,只要测量哪些量?为什么?
抽象
把两根钢条的中点
连在一起
转化
AO=CO , BO=DO.
测量工件内槽宽AB
转化
求与AB相等的线段.
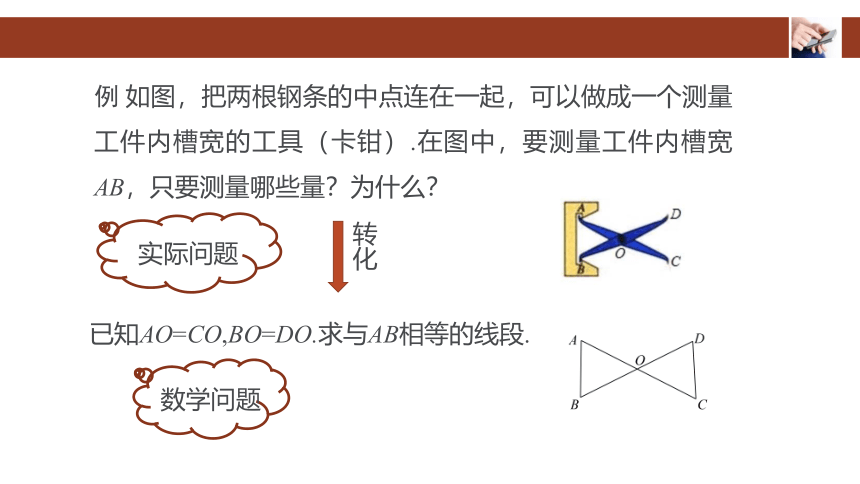
例 如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳).在图中,要测量工件内槽宽AB,只要测量哪些量?为什么?
实际问题
已知AO=CO,BO=DO.求与AB相等的线段.
数学问题
转化
解:只需测量CD.
∵点O是AC、BD的中点,
∴OA=OC,OB=OD.
在△AOB和△COD中,
∴△AOB≌△COD (SAS).
∴CD=AB.
∴要测量槽内宽AB,只需测量CD.
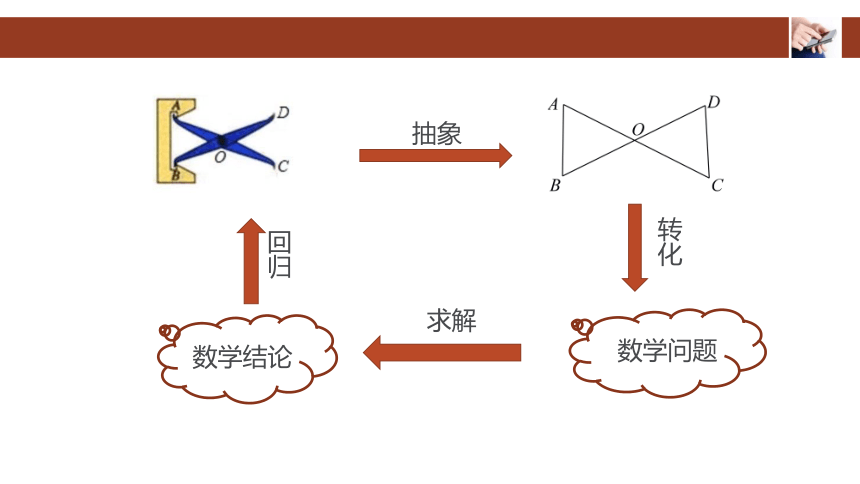
抽象
数学问题
转化
求解
数学结论
回归
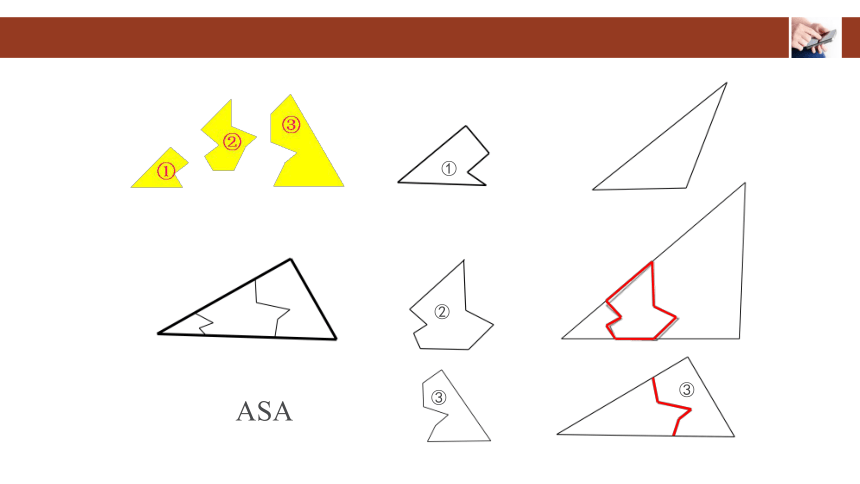
例 如图,某同学把一块三角形的玻璃打碎成了三块,现在
要到玻璃店去配一块完全一样的玻璃,那么最合理的办法是拿( )去配.
①
②
③
ASA
③
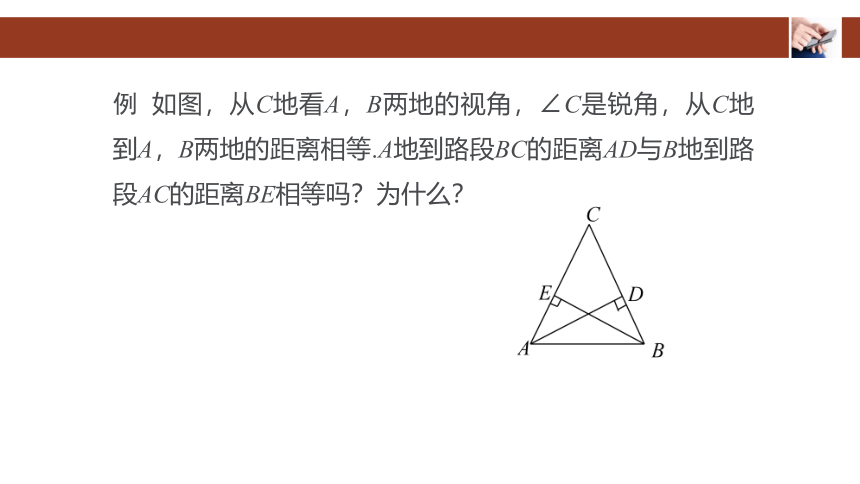
例 如图,从C地看A,B两地的视角,∠C是锐角,从C地到A,B两地的距离相等.A地到路段BC的距离AD与B地到路段AC的距离BE相等吗?为什么?
例 如图,从C地看A,B两地的视角,∠C是锐角,从C地到A,B两地的距离相等.A地到路段BC的距离AD与B地到路段AC的距离BE相等吗?为什么?
证明:∵AD⊥BC, BE⊥AC,
∴ ∠CDA= ∠CEB=90°.
在△ADC和△BEC中,
∴△CDA≌△CEB (AAS).
∴AD=BE.
∴A地到路段BC的距离AD与
B地到路段AC的距离BE相等.
练习 如图,两车从路段AB的两端同时出发,沿平行路线以相同的速度行驶,相同时间后分别到达C,D两地.C,D两地到路段AB的距离相等吗?为什么?
练习 如图,两车从路段AB的两端同时出发,沿平行路线以相同的速度行驶,相同时间后分别到达C,D两地.C,D两地到路段AB的距离相等吗?为什么?
已知AC∥BD,且AC=BD.
CE⊥AB,DF⊥AB.
CE与DF是否相等?
已知AC∥BD,且AC=BD.
CE⊥AB,DF⊥AB.
CE与AB是否相等?
证明:∵CE⊥AB,DF⊥AB,
∴∠AEC=∠BFD=90°.
∴△AEC≌△BFD (AAS).
∵AC∥BD,
∴∠A=∠B.
在△AEC与△BFD中,
∴ C,D两地到路段AB的距离相等.
∴CE=DF.
答:相等
例 如图,AC和BD是两根旗杆,两根旗杆间相距12 m,某人从点B沿BA走向A,一定时间他到达点M,此时他仰望旗杆的顶点C和D,两次视线夹角为90°,且CM=DM,已知旗杆AC的高为3 m,该人的运动速度为1 m/s,求这个人运动了多长时间?
?
例 如图,AC和BD是两根旗杆,两根旗杆间相距12 m,某人从点B沿BA走向A,一定时间他到达点M,此时他仰望旗杆的顶点C和D,两次视线夹角为90°,且CM=DM,已知旗杆AC的高为3 m,该人的运动速度为1 m/s,求这个人运动了多长时间?
?
解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°.
又∵∠CAM=90°,
∴∠CMA+∠ACM=90°.
∴∠ACM=∠BMD.
∴△AMC≌△BDM (AAS).
在△AMC与△BDM中,
∴他到达点M时,运动时间为3 s.
∴AC=BM=3 m.
3÷1=3 s
例 小春在做数学作业时,遇到这样一个问题:如图,AB=CD,BC=AD,请说明∠A=∠C.小春动手测量了一下,发现∠A确实等于∠C,但她不能说明其中的道理,你能
帮助她吗?
例 小春在做数学作业时,遇到这样一个问题:如图,AB=CD,BC=AD,请说明∠A=∠C.小春动手测量了一下,发现∠A确实等于∠C,但她不能说明其中的道理,你能帮助她吗?
在△ABD和△CDB中,
∴△ABD≌△CDB(SSS).
∴∠A=∠C.
连接BD.
抽象
数学问题
转化
求解
数学结论
回归
实际问题
数学模型
课堂小结
课后作业
1.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC 和∠DEF 的大小有什么关系?为什么? ?
2.如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,此时,DA⊥AB,EB⊥AB,D、E与路段AB的距离相等吗?为什么?
课后作业
同学们,再见!
(第三课时)
例 如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳). 在图中,要测量工件内槽宽AB,只要测量哪些量?为什么?
抽象
把两根钢条的中点
连在一起
转化
AO=CO , BO=DO.
测量工件内槽宽AB
转化
求与AB相等的线段.
例 如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳).在图中,要测量工件内槽宽AB,只要测量哪些量?为什么?
实际问题
已知AO=CO,BO=DO.求与AB相等的线段.
数学问题
转化
解:只需测量CD.
∵点O是AC、BD的中点,
∴OA=OC,OB=OD.
在△AOB和△COD中,
∴△AOB≌△COD (SAS).
∴CD=AB.
∴要测量槽内宽AB,只需测量CD.
抽象
数学问题
转化
求解
数学结论
回归
例 如图,某同学把一块三角形的玻璃打碎成了三块,现在
要到玻璃店去配一块完全一样的玻璃,那么最合理的办法是拿( )去配.
①
②
③
ASA
③
例 如图,从C地看A,B两地的视角,∠C是锐角,从C地到A,B两地的距离相等.A地到路段BC的距离AD与B地到路段AC的距离BE相等吗?为什么?
例 如图,从C地看A,B两地的视角,∠C是锐角,从C地到A,B两地的距离相等.A地到路段BC的距离AD与B地到路段AC的距离BE相等吗?为什么?
证明:∵AD⊥BC, BE⊥AC,
∴ ∠CDA= ∠CEB=90°.
在△ADC和△BEC中,
∴△CDA≌△CEB (AAS).
∴AD=BE.
∴A地到路段BC的距离AD与
B地到路段AC的距离BE相等.
练习 如图,两车从路段AB的两端同时出发,沿平行路线以相同的速度行驶,相同时间后分别到达C,D两地.C,D两地到路段AB的距离相等吗?为什么?
练习 如图,两车从路段AB的两端同时出发,沿平行路线以相同的速度行驶,相同时间后分别到达C,D两地.C,D两地到路段AB的距离相等吗?为什么?
已知AC∥BD,且AC=BD.
CE⊥AB,DF⊥AB.
CE与DF是否相等?
已知AC∥BD,且AC=BD.
CE⊥AB,DF⊥AB.
CE与AB是否相等?
证明:∵CE⊥AB,DF⊥AB,
∴∠AEC=∠BFD=90°.
∴△AEC≌△BFD (AAS).
∵AC∥BD,
∴∠A=∠B.
在△AEC与△BFD中,
∴ C,D两地到路段AB的距离相等.
∴CE=DF.
答:相等
例 如图,AC和BD是两根旗杆,两根旗杆间相距12 m,某人从点B沿BA走向A,一定时间他到达点M,此时他仰望旗杆的顶点C和D,两次视线夹角为90°,且CM=DM,已知旗杆AC的高为3 m,该人的运动速度为1 m/s,求这个人运动了多长时间?
?
例 如图,AC和BD是两根旗杆,两根旗杆间相距12 m,某人从点B沿BA走向A,一定时间他到达点M,此时他仰望旗杆的顶点C和D,两次视线夹角为90°,且CM=DM,已知旗杆AC的高为3 m,该人的运动速度为1 m/s,求这个人运动了多长时间?
?
解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°.
又∵∠CAM=90°,
∴∠CMA+∠ACM=90°.
∴∠ACM=∠BMD.
∴△AMC≌△BDM (AAS).
在△AMC与△BDM中,
∴他到达点M时,运动时间为3 s.
∴AC=BM=3 m.
3÷1=3 s
例 小春在做数学作业时,遇到这样一个问题:如图,AB=CD,BC=AD,请说明∠A=∠C.小春动手测量了一下,发现∠A确实等于∠C,但她不能说明其中的道理,你能
帮助她吗?
例 小春在做数学作业时,遇到这样一个问题:如图,AB=CD,BC=AD,请说明∠A=∠C.小春动手测量了一下,发现∠A确实等于∠C,但她不能说明其中的道理,你能帮助她吗?
在△ABD和△CDB中,
∴△ABD≌△CDB(SSS).
∴∠A=∠C.
连接BD.
抽象
数学问题
转化
求解
数学结论
回归
实际问题
数学模型
课堂小结
课后作业
1.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC 和∠DEF 的大小有什么关系?为什么? ?
2.如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,此时,DA⊥AB,EB⊥AB,D、E与路段AB的距离相等吗?为什么?
课后作业
同学们,再见!
