人教版八年级上册12.2全等三角形的性质与判定的综合运用(第一课时)课件(30张)
文档属性
| 名称 | 人教版八年级上册12.2全等三角形的性质与判定的综合运用(第一课时)课件(30张) |  | |
| 格式 | pptx | ||
| 文件大小 | 296.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:01:42 | ||
图片预览

文档简介
全等三角形的性质与判定的综合运用
(第一课时)
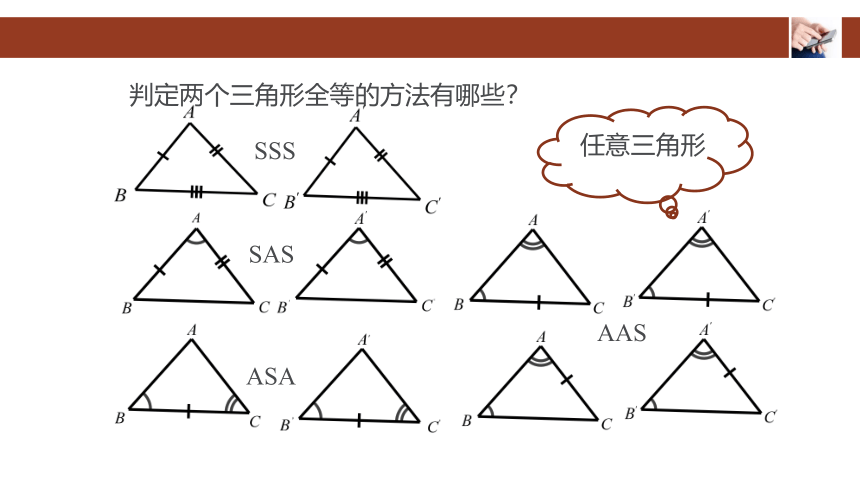
判定两个三角形全等的方法有哪些?
SSS
SAS
ASA
AAS
任意三角形
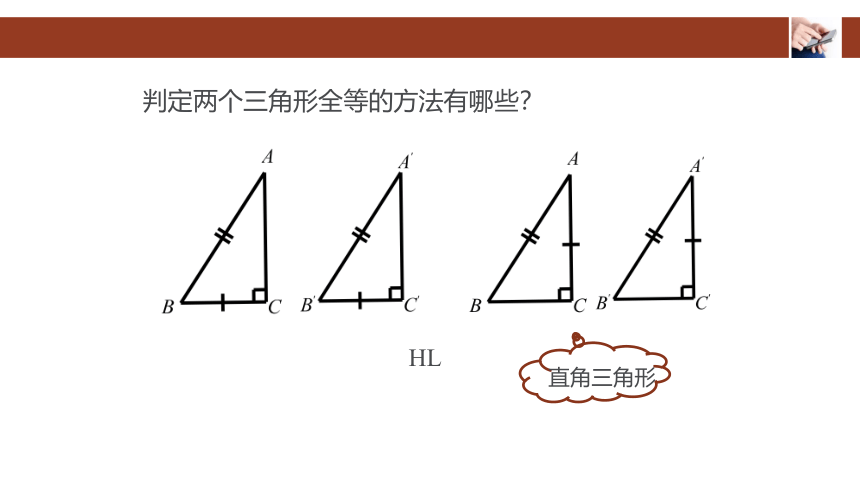
判定两个三角形全等的方法有哪些?
HL
直角三角形
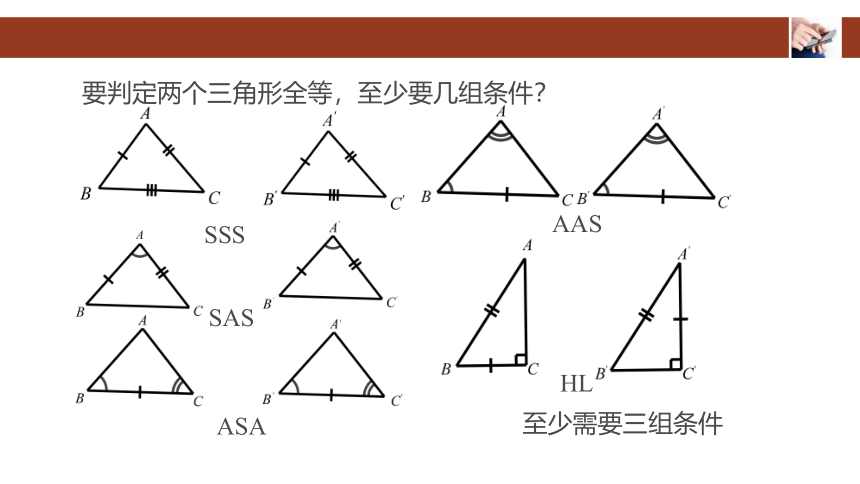
要判定两个三角形全等,至少要几组条件?
SSS
SAS
ASA
AAS
HL
至少需要三组条件
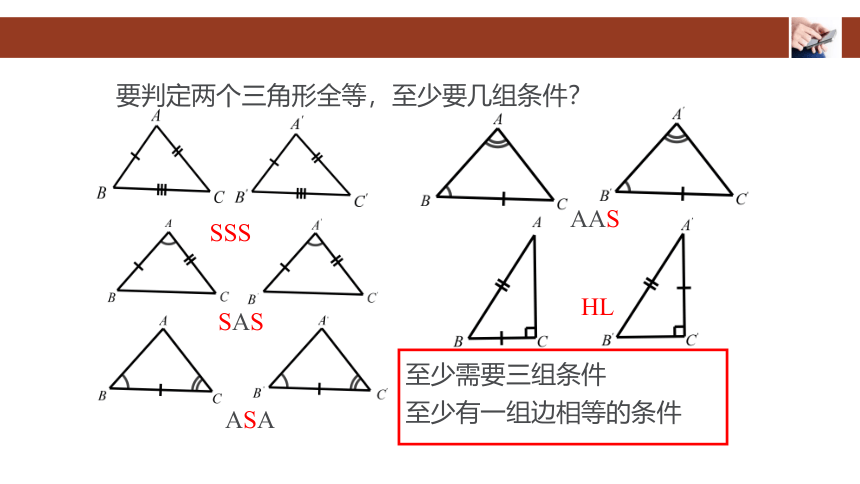
要判定两个三角形全等,至少要几组条件?
SSS
SAS
ASA
AAS
HL
至少需要三组条件
至少有一组边相等的条件
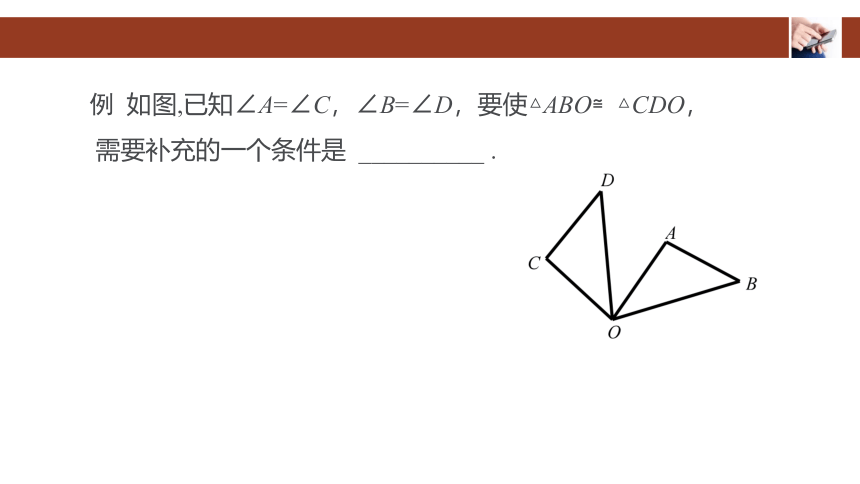
例 如图,已知∠A=∠C,∠B=∠D,要使△ABO≌△CDO,
需要补充的一个条件是 __________ .
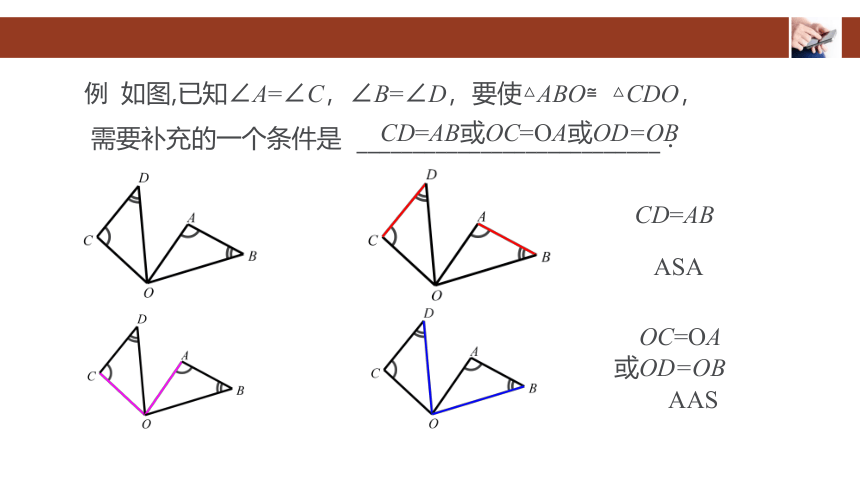
例 如图,已知∠A=∠C,∠B=∠D,要使△ABO≌△CDO,
需要补充的一个条件是 ___________________________ .
CD=AB
ASA
OC=OA
或OD=OB
AAS
CD=AB或OC=OA或OD=OB
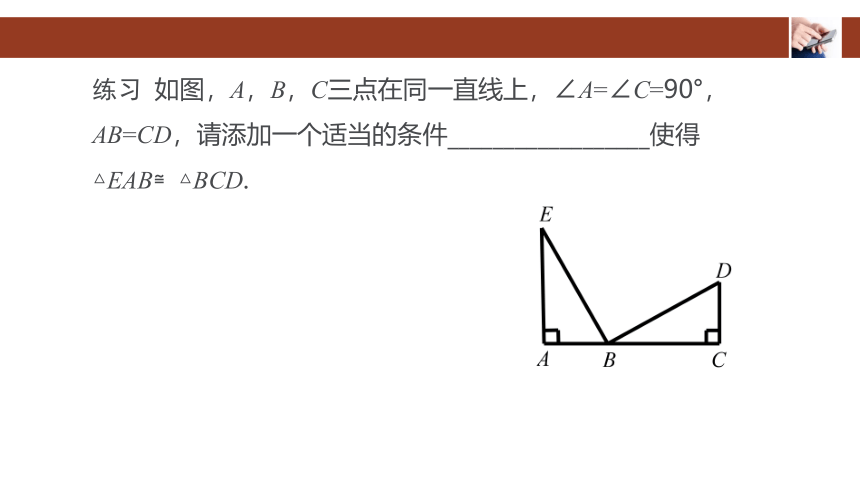
练习 如图,A,B,C三点在同一直线上,∠A=∠C=90°,
AB=CD,请添加一个适当的条件__________________使得
△EAB≌△BCD.
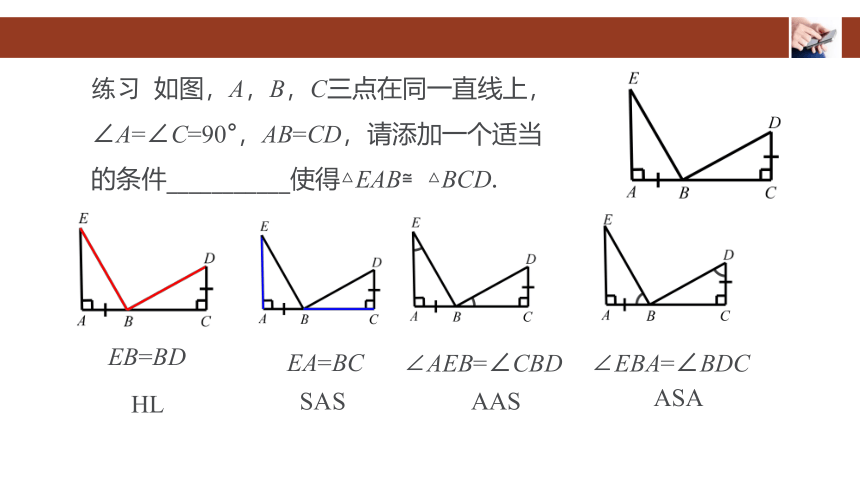
EB=BD
HL
EA=BC
SAS
∠AEB=∠CBD
∠EBA=∠BDC
AAS
ASA
练习 如图,A,B,C三点在同一直线上,
∠A=∠C=90°,AB=CD,请添加一个适当
的条件___________使得△EAB≌△BCD.
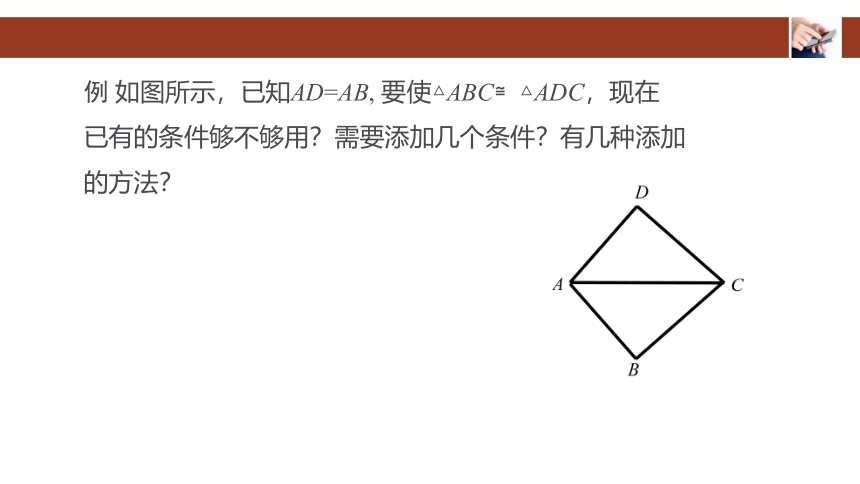
例 如图所示,已知AD=AB, 要使△ABC≌△ADC,现在
已有的条件够不够用?需要添加几个条件?有几种添加
的方法??
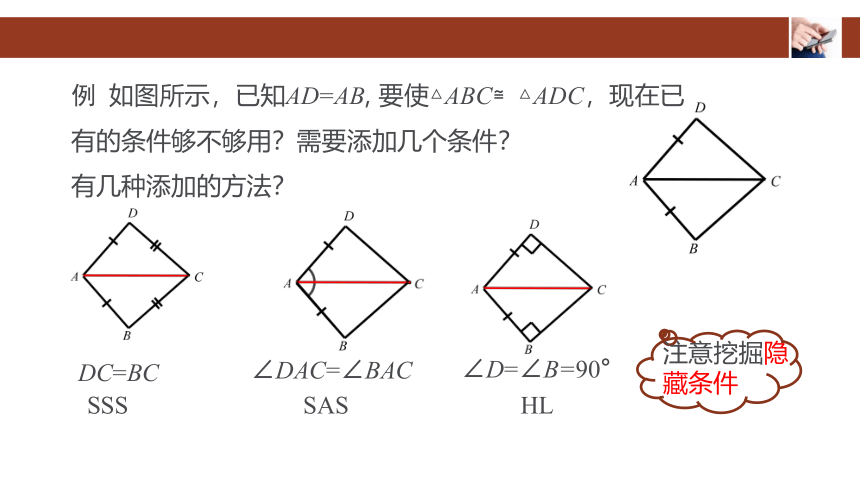
例 如图所示,已知AD=AB, 要使△ABC≌△ADC,现在已有的条件够不够用?需要添加几个条件?
有几种添加的方法??
DC=BC
SSS
∠DAC=∠BAC
SAS
∠D=∠B=90°
HL
注意挖掘隐藏条件
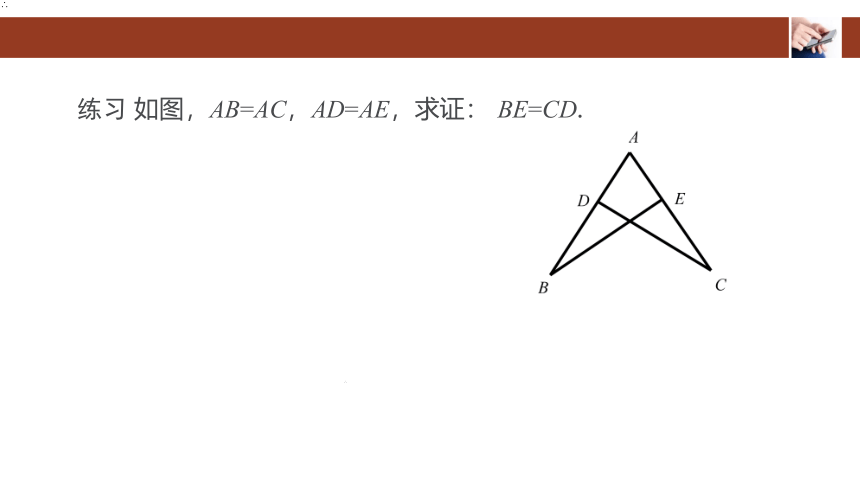
练习 如图,AB=AC,AD=AE,求证: BE=CD.
练习 如图,AB=AC,AD=AE,求证: BE=CD.
分析:已知AB=AC,AD=AE,有公共角∠A,并且公共角是两边的夹角.
证明:在△ABE和△ACD中,
∴△ABE≌△ACD (SAS)
∴ BE=CD .
例 如图,点B,E,C,F在一条直线上,AB=DE , AC=DF,
BE=CF,求证:∠A=∠D .
例 如图,点B,E,C,F在一条直线上,AB=DE , AC=DF,
BE=CF,求证:∠A=∠D .
证明:∵BE=CF,
∴BE+EC=CF+EC.
即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
∴∠A=∠D .
例 如图,点B,E,C,F在一条直线上,AB=DE , AC=DF,
BE=CF,求证:∠A=∠D .
例 如图,在△ABC和△ADE中,∠BAC=∠DAE,AD=AE.
连接BD,CE,∠ABD=∠ACE. 求证:AB=AC.
分析:
要证AB=AC
需证△BAD≌△CAE
已知∠BAC=∠DAE , AD=AE,∠ABD=∠ACE.
∠BAC -∠CAD=∠DAE-∠CAD
∠BAD=∠CAE
AAS
证明:∵∠BAC=∠DAE,
∴∠BAC-∠CAD=∠DAE-∠CAD.
即∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(AAS) .
∴AB=AC.
当出现点共线、角共顶点时,
经常会用到等量相加结果相等、等量相减结果相等,这也是求两条边、两个角相等经常用到的方法.?
?
练习 如图,B,F,C,E在一条直线上, BF=CE,AC=DF .
(1)在下列条件①∠B=∠E;②∠ACB=∠DFE;③AB=DE;
④AC∥DF中,只添加一个条件就可以证得△ABC≌△DEF,
则所有正确条件的序号是 _______________.
(2)根据已知及(1)中添加的一个条件证明∠A=∠D .
练习 如图,B,F,C,E在一条直线上, BF=CE,AC=DF .
(1)在下列条件①∠B=∠E;②∠ACB=∠DFE;③AB=DE;
④AC∥DF中,只添加一个条件就可以证得△ABC≌△DEF,
则所有正确条件的序号是 _____________.
练习 如图,B,F,C,E在一条直线上, BF=CE,AC=DF .
(1)在下列条件①∠B=∠E;②∠ACB=∠DFE;③AB=DE;
④AC∥DF中,只添加一个条件就可以证得△ABC≌△DEF,
则所有正确条件的序号是 _____.
BF+FC=CE+FC
练习 如图,B,F,C,E在一条直线上, BF=CE,AC=DF .
(1)在下列条件①∠B=∠E;②∠ACB=∠DFE;③AB=DE;
④AC∥DF中,只添加一个条件就可以证得△ABC≌△DEF,
则所有正确条件的序号是 __________.
练习 如图,B,F,C,E在一条直线上, BF=CE,AC=DF .
(1)在下列条件①∠B=∠E;②∠ACB=∠DFE;③AB=DE;
④AC∥DF中,只添加一个条件就可以证得△ABC≌△DEF,
则所有正确条件的序号是 __________.
练习 如图,B,F,C,E在一条直线上, BF=CE,AC=DF .
(1)在下列条件①∠B=∠E;②∠ACB=∠DFE;③AB=DE;
④AC∥DF中,只添加一个条件就可以证得△ABC≌△DEF,
则所有正确条件的序号是 __________.
练习 如图,B,F,C,E在一条直线上, BF=CE,AC=DF .
(1)在下列条件①∠B=∠E;②∠ACB=∠DFE;③AB=DE;
④AC∥DF中,只添加一个条件就可以证得△ABC≌△DEF,
则所有正确条件的序号是 ____________.
② ③ ④
练习 如图,B,F,C,E在一条直线上, BF=CE,AC=DF .
(2)根据已知及(1)中添加的一个条件证明∠A=∠D .
添加②∠ACB=∠DFE为例证明
∵BF=CE,
∴ EF+FC=CE+FC.
即BC=EF.
在△ABC和△DEF中,
?
AC=DF ,
∠ACB=∠DFE ,
BC=EF ,
∴ △ABC≌△DEF (SAS).
∴∠A=∠D .
1 几何题解题习惯
依题意标图、关注图形特征、挖掘隐藏条件.
3 几何题解题思路
从结论入手,结合已知,双向推理.
课堂小结
2 三角形全等知识
巩固判定方法,根据已知条件灵活选择判定方法.
1.如图,点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.求证:(1)AD=AE; (2)BD=CE.
课后作业
课后作业
2. 如图,点B、E、C、F在一条直线上,AC=DF,AC=DF,∠A=∠D.求证:BE=CF.
同学们,再见!
(第一课时)
判定两个三角形全等的方法有哪些?
SSS
SAS
ASA
AAS
任意三角形
判定两个三角形全等的方法有哪些?
HL
直角三角形
要判定两个三角形全等,至少要几组条件?
SSS
SAS
ASA
AAS
HL
至少需要三组条件
要判定两个三角形全等,至少要几组条件?
SSS
SAS
ASA
AAS
HL
至少需要三组条件
至少有一组边相等的条件
例 如图,已知∠A=∠C,∠B=∠D,要使△ABO≌△CDO,
需要补充的一个条件是 __________ .
例 如图,已知∠A=∠C,∠B=∠D,要使△ABO≌△CDO,
需要补充的一个条件是 ___________________________ .
CD=AB
ASA
OC=OA
或OD=OB
AAS
CD=AB或OC=OA或OD=OB
练习 如图,A,B,C三点在同一直线上,∠A=∠C=90°,
AB=CD,请添加一个适当的条件__________________使得
△EAB≌△BCD.
EB=BD
HL
EA=BC
SAS
∠AEB=∠CBD
∠EBA=∠BDC
AAS
ASA
练习 如图,A,B,C三点在同一直线上,
∠A=∠C=90°,AB=CD,请添加一个适当
的条件___________使得△EAB≌△BCD.
例 如图所示,已知AD=AB, 要使△ABC≌△ADC,现在
已有的条件够不够用?需要添加几个条件?有几种添加
的方法??
例 如图所示,已知AD=AB, 要使△ABC≌△ADC,现在已有的条件够不够用?需要添加几个条件?
有几种添加的方法??
DC=BC
SSS
∠DAC=∠BAC
SAS
∠D=∠B=90°
HL
注意挖掘隐藏条件
练习 如图,AB=AC,AD=AE,求证: BE=CD.
练习 如图,AB=AC,AD=AE,求证: BE=CD.
分析:已知AB=AC,AD=AE,有公共角∠A,并且公共角是两边的夹角.
证明:在△ABE和△ACD中,
∴△ABE≌△ACD (SAS)
∴ BE=CD .
例 如图,点B,E,C,F在一条直线上,AB=DE , AC=DF,
BE=CF,求证:∠A=∠D .
例 如图,点B,E,C,F在一条直线上,AB=DE , AC=DF,
BE=CF,求证:∠A=∠D .
证明:∵BE=CF,
∴BE+EC=CF+EC.
即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
∴∠A=∠D .
例 如图,点B,E,C,F在一条直线上,AB=DE , AC=DF,
BE=CF,求证:∠A=∠D .
例 如图,在△ABC和△ADE中,∠BAC=∠DAE,AD=AE.
连接BD,CE,∠ABD=∠ACE. 求证:AB=AC.
分析:
要证AB=AC
需证△BAD≌△CAE
已知∠BAC=∠DAE , AD=AE,∠ABD=∠ACE.
∠BAC -∠CAD=∠DAE-∠CAD
∠BAD=∠CAE
AAS
证明:∵∠BAC=∠DAE,
∴∠BAC-∠CAD=∠DAE-∠CAD.
即∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(AAS) .
∴AB=AC.
当出现点共线、角共顶点时,
经常会用到等量相加结果相等、等量相减结果相等,这也是求两条边、两个角相等经常用到的方法.?
?
练习 如图,B,F,C,E在一条直线上, BF=CE,AC=DF .
(1)在下列条件①∠B=∠E;②∠ACB=∠DFE;③AB=DE;
④AC∥DF中,只添加一个条件就可以证得△ABC≌△DEF,
则所有正确条件的序号是 _______________.
(2)根据已知及(1)中添加的一个条件证明∠A=∠D .
练习 如图,B,F,C,E在一条直线上, BF=CE,AC=DF .
(1)在下列条件①∠B=∠E;②∠ACB=∠DFE;③AB=DE;
④AC∥DF中,只添加一个条件就可以证得△ABC≌△DEF,
则所有正确条件的序号是 _____________.
练习 如图,B,F,C,E在一条直线上, BF=CE,AC=DF .
(1)在下列条件①∠B=∠E;②∠ACB=∠DFE;③AB=DE;
④AC∥DF中,只添加一个条件就可以证得△ABC≌△DEF,
则所有正确条件的序号是 _____.
BF+FC=CE+FC
练习 如图,B,F,C,E在一条直线上, BF=CE,AC=DF .
(1)在下列条件①∠B=∠E;②∠ACB=∠DFE;③AB=DE;
④AC∥DF中,只添加一个条件就可以证得△ABC≌△DEF,
则所有正确条件的序号是 __________.
练习 如图,B,F,C,E在一条直线上, BF=CE,AC=DF .
(1)在下列条件①∠B=∠E;②∠ACB=∠DFE;③AB=DE;
④AC∥DF中,只添加一个条件就可以证得△ABC≌△DEF,
则所有正确条件的序号是 __________.
练习 如图,B,F,C,E在一条直线上, BF=CE,AC=DF .
(1)在下列条件①∠B=∠E;②∠ACB=∠DFE;③AB=DE;
④AC∥DF中,只添加一个条件就可以证得△ABC≌△DEF,
则所有正确条件的序号是 __________.
练习 如图,B,F,C,E在一条直线上, BF=CE,AC=DF .
(1)在下列条件①∠B=∠E;②∠ACB=∠DFE;③AB=DE;
④AC∥DF中,只添加一个条件就可以证得△ABC≌△DEF,
则所有正确条件的序号是 ____________.
② ③ ④
练习 如图,B,F,C,E在一条直线上, BF=CE,AC=DF .
(2)根据已知及(1)中添加的一个条件证明∠A=∠D .
添加②∠ACB=∠DFE为例证明
∵BF=CE,
∴ EF+FC=CE+FC.
即BC=EF.
在△ABC和△DEF中,
?
AC=DF ,
∠ACB=∠DFE ,
BC=EF ,
∴ △ABC≌△DEF (SAS).
∴∠A=∠D .
1 几何题解题习惯
依题意标图、关注图形特征、挖掘隐藏条件.
3 几何题解题思路
从结论入手,结合已知,双向推理.
课堂小结
2 三角形全等知识
巩固判定方法,根据已知条件灵活选择判定方法.
1.如图,点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.求证:(1)AD=AE; (2)BD=CE.
课后作业
课后作业
2. 如图,点B、E、C、F在一条直线上,AC=DF,AC=DF,∠A=∠D.求证:BE=CF.
同学们,再见!
