人教版八年级上册12.2再探三角形全等的条件课件(19张)
文档属性
| 名称 | 人教版八年级上册12.2再探三角形全等的条件课件(19张) |  | |
| 格式 | pptx | ||
| 文件大小 | 254.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:02:22 | ||
图片预览




文档简介
再探三角形全等的条件
课前准备
铅笔,白纸,圆规,直尺.
1 根据定义
由全等三角形的定义可知,满足三条边分别相等,三个角分别相等的两个三角形全等
3 提出问题
2 探究方向
用较少的条件,就能简洁地判断两个三角形全等,那会是几组条件呢——三组
从边、角出发,满足三组条件的所有情况,我们是否在之前的学习中都讨论完全了呢?
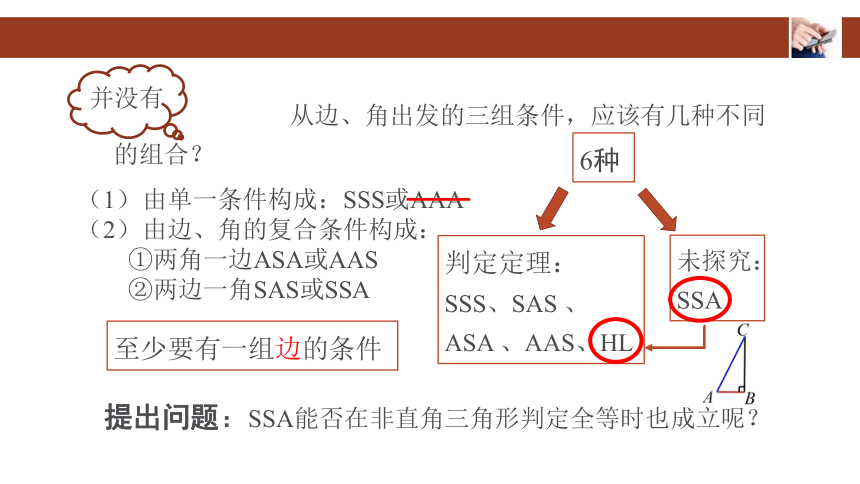
并没有
(1) 由单一条件构成:SSS或AAA
(2) 由边、角的复合条件构成:
①两角一边ASA或AAS
②两边一角SAS或SSA
从边、角出发的三组条件,应该有几种不同的组合?
6种
至少要有一组边的条件
判定定理:
SSS、SAS 、 ASA 、AAS、HL
未探究:
SSA
提出问题:SSA能否在非直角三角形判定全等时也成立呢?
提出猜想:两组边及一边的对角分别相等的两个三角形全等.
三角形的全等条件就是确定三角形的形状和大小的条件.
等价猜想:两边一对角是否能确定三角形的形状和大小.
转化
已知:在三角形中,两边为a,b,边a的对角为α.
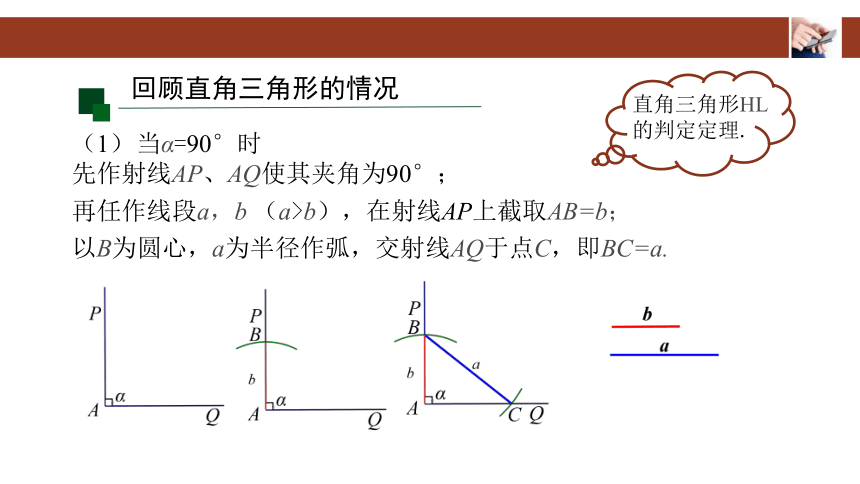
(1) 当α=90°时
先作射线AP、AQ使其夹角为90°;
回顾直角三角形的情况
再任作线段a,b (a>b),在射线AP上截取AB=b;
以B为圆心,a为半径作弧,交射线AQ于点C,即BC=a.
直角三角形HL的判定定理.
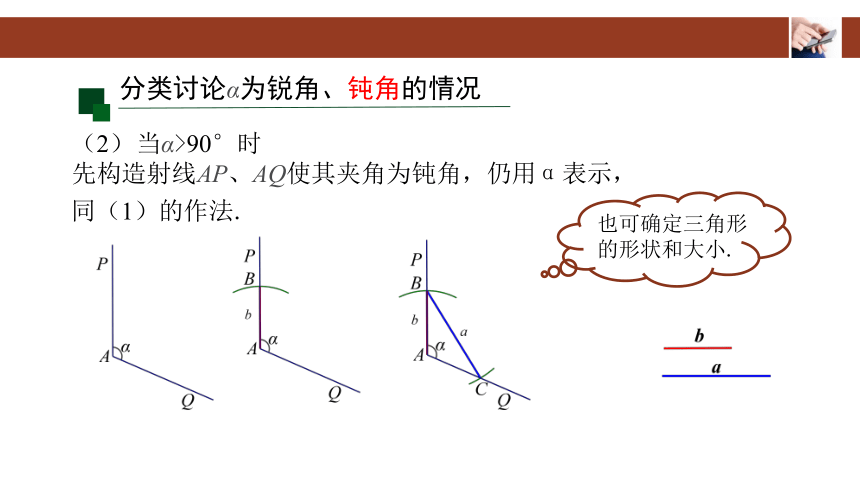
(2) 当α>90°时
先构造射线AP、AQ使其夹角为钝角,仍用α表示,
分类讨论α为锐角、钝角的情况
同(1)的作法.
也可确定三角形的形状和大小.
(3) 当α<90°时
沿用上面的作图经验,我们容易得到下图,且也是唯一的.
分类讨论α为锐角、钝角的情况
猜想“似乎” 是正确的!
小结目前的研究
寻找共性,归纳结论
两边分别相等且两边中大边的对角也分别相等的两个三角形全等(简记为“SSA(1)”).
我们的结论
(3) 当α<90°时
α有可能不再是图中的最大角,它对的边,可以不是最长边.
α为锐角时,我们忽略了什么?
α<90°
α 不一定是最大角
α>90°
α 为最大角,a为最长边
α=90°
α 为最大角,a为最长边
对于边a、b的讨论,还没有完全
(3) 当α<90°时,忽略了a=b, aα为锐角时,我们继续探究
让a保持不变,让b逐渐变大.
a=b时,
三角形唯一
a三角形不唯一
a>b时,
三角形唯一
×
(3) 当α<90°时,aα为锐角时, b继续变大.
aaa√
×
×
当α≥90°时
aa=AC边上的高
当α<90°时
a≥b
归纳——SSA成立的情况
√
当α<90°时
归纳——SSA不成立的情况×
aa出现两个三角形,△ABC1和△ABC2
没有唯一确定三角形.
三角形不存在
当α<90°时
不严谨的SSA
×
×
当α≥90°时
HL
在b连续变化中进行讨论
SSA不具有普适性.
不能成为判定定理
条件超过3组,可以“放心” 判定全等吗?
×
曾经有一位中学的数学教师向数学家赵访熊教授请教:如果一个三角形,有五个元素与另一个三角形的五个元素两两相等,这两个三角形是否全等?
没问题吧……
小结
探究的过程、分类的依据、讨论的过程都非常有意义.
没有探究出新的方法来判定两个三角形全等.
但发现SSA在哪些情形下,可以判定两个三角形全等.
发现问题提出问题
角的锐钝边的长短
顺序有序连续变化
V.S.
作业
1. 阅读教材P46-47
2. 借助几何画板,或通过尺规作图,试着复盘今天探究的 过程,把你的发现,整理在作业本上.
同学们,再见!
课前准备
铅笔,白纸,圆规,直尺.
1 根据定义
由全等三角形的定义可知,满足三条边分别相等,三个角分别相等的两个三角形全等
3 提出问题
2 探究方向
用较少的条件,就能简洁地判断两个三角形全等,那会是几组条件呢——三组
从边、角出发,满足三组条件的所有情况,我们是否在之前的学习中都讨论完全了呢?
并没有
(1) 由单一条件构成:SSS或AAA
(2) 由边、角的复合条件构成:
①两角一边ASA或AAS
②两边一角SAS或SSA
从边、角出发的三组条件,应该有几种不同的组合?
6种
至少要有一组边的条件
判定定理:
SSS、SAS 、 ASA 、AAS、HL
未探究:
SSA
提出问题:SSA能否在非直角三角形判定全等时也成立呢?
提出猜想:两组边及一边的对角分别相等的两个三角形全等.
三角形的全等条件就是确定三角形的形状和大小的条件.
等价猜想:两边一对角是否能确定三角形的形状和大小.
转化
已知:在三角形中,两边为a,b,边a的对角为α.
(1) 当α=90°时
先作射线AP、AQ使其夹角为90°;
回顾直角三角形的情况
再任作线段a,b (a>b),在射线AP上截取AB=b;
以B为圆心,a为半径作弧,交射线AQ于点C,即BC=a.
直角三角形HL的判定定理.
(2) 当α>90°时
先构造射线AP、AQ使其夹角为钝角,仍用α表示,
分类讨论α为锐角、钝角的情况
同(1)的作法.
也可确定三角形的形状和大小.
(3) 当α<90°时
沿用上面的作图经验,我们容易得到下图,且也是唯一的.
分类讨论α为锐角、钝角的情况
猜想“似乎” 是正确的!
小结目前的研究
寻找共性,归纳结论
两边分别相等且两边中大边的对角也分别相等的两个三角形全等(简记为“SSA(1)”).
我们的结论
(3) 当α<90°时
α有可能不再是图中的最大角,它对的边,可以不是最长边.
α为锐角时,我们忽略了什么?
α<90°
α 不一定是最大角
α>90°
α 为最大角,a为最长边
α=90°
α 为最大角,a为最长边
对于边a、b的讨论,还没有完全
(3) 当α<90°时,忽略了a=b, a
让a保持不变,让b逐渐变大.
a=b时,
三角形唯一
a
a>b时,
三角形唯一
×
(3) 当α<90°时,a
a
×
×
当α≥90°时
a
当α<90°时
a≥b
归纳——SSA成立的情况
√
当α<90°时
归纳——SSA不成立的情况×
a
没有唯一确定三角形.
三角形不存在
当α<90°时
不严谨的SSA
×
×
当α≥90°时
HL
在b连续变化中进行讨论
SSA不具有普适性.
不能成为判定定理
条件超过3组,可以“放心” 判定全等吗?
×
曾经有一位中学的数学教师向数学家赵访熊教授请教:如果一个三角形,有五个元素与另一个三角形的五个元素两两相等,这两个三角形是否全等?
没问题吧……
小结
探究的过程、分类的依据、讨论的过程都非常有意义.
没有探究出新的方法来判定两个三角形全等.
但发现SSA在哪些情形下,可以判定两个三角形全等.
发现问题提出问题
角的锐钝边的长短
顺序有序连续变化
V.S.
作业
1. 阅读教材P46-47
2. 借助几何画板,或通过尺规作图,试着复盘今天探究的 过程,把你的发现,整理在作业本上.
同学们,再见!
