人教版八年级上册12.2三角形全等的判定——HL课件(24张)
文档属性
| 名称 | 人教版八年级上册12.2三角形全等的判定——HL课件(24张) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:03:43 | ||
图片预览



文档简介
三角形全的判定——HL
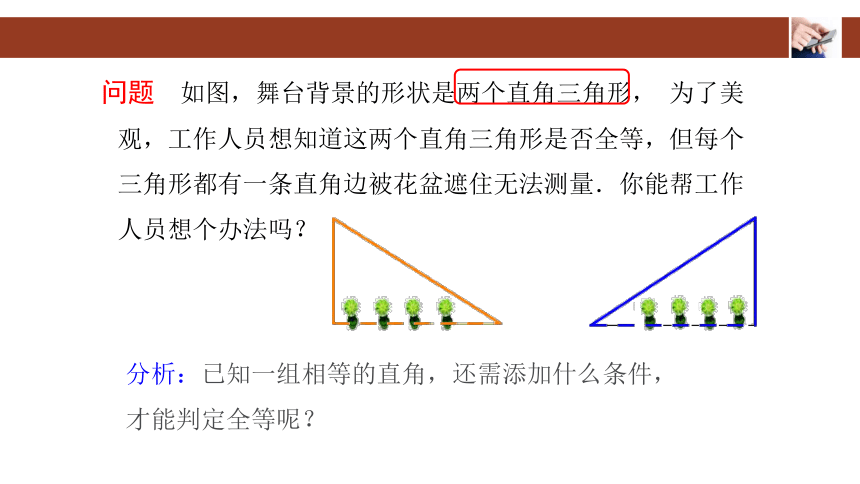
问题 如图,舞台背景的形状是两个直角三角形, 为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.你能帮工作人员想个办法吗?
分析:已知一组相等的直角,还需添加什么条件,才能判定全等呢?
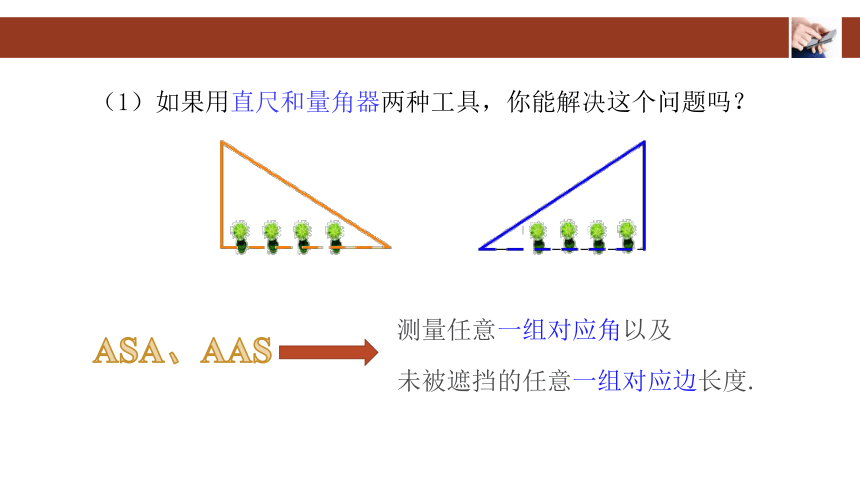
(1)如果用直尺和量角器两种工具,你能解决这个问题吗?
测量任意一组对应角以及
未被遮挡的任意一组对应边长度.
ASA、AAS
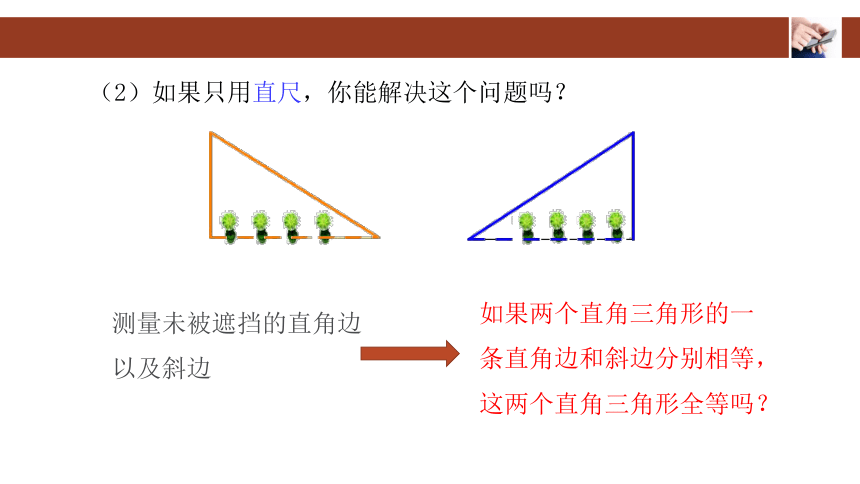
(2)如果只用直尺,你能解决这个问题吗?
测量未被遮挡的直角边以及斜边
如果两个直角三角形的一条直角边和斜边分别相等,这两个直角三角形全等吗?
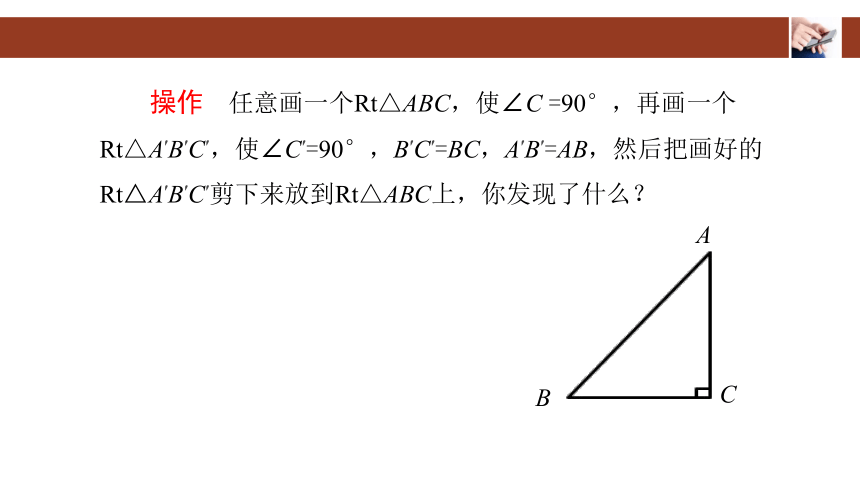
操作 任意画一个Rt△ABC,使∠C =90°,再画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,A′B′=AB,然后把画好的Rt△A′B′C′剪下来放到Rt△ABC上,你发现了什么?
A
B
C
现象:两个三角形放在一起能完全重合.
说明:这两个三角形全等.
条件:∠C=∠C′=90°,B′C′=BC,A′B′=AB
“HL”判定方法:
斜边和一条直角边分别相等的两个直角三角形全等
(简写为“斜边、直角边”或“HL”).
N
M
C′
A
B
C
A′
B′
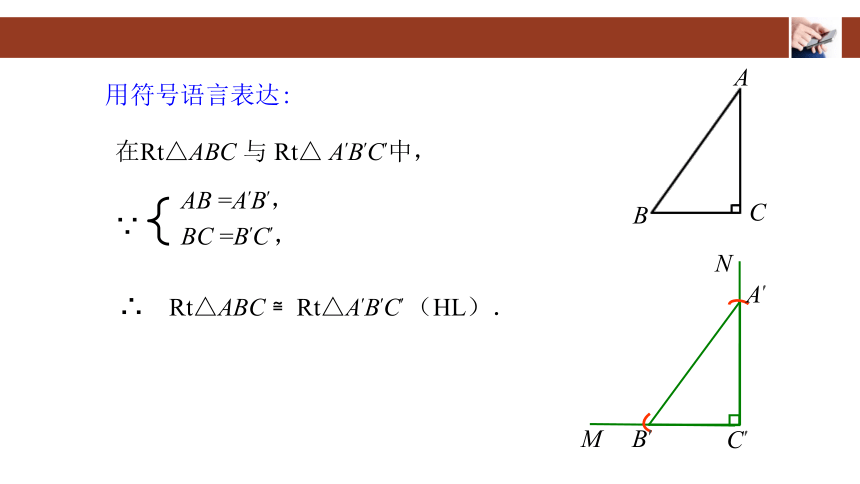
用符号语言表达:
在Rt△ABC 与 Rt△ A′B′C′中,
∴ Rt△ABC ≌Rt△A′B′C′ (HL).
AB =A′B′,
BC =B′C′,
∵
N
M
C′
A
B
C
A′
B′
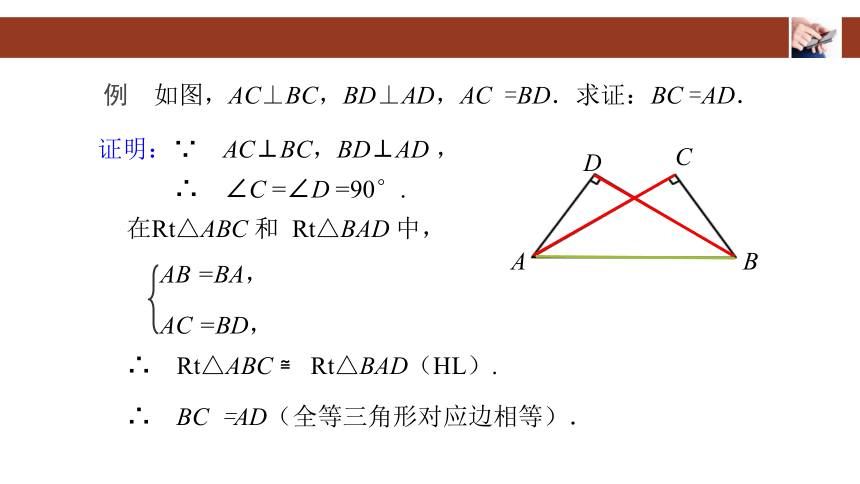
例 如图,AC⊥BC,BD⊥AD,AC =BD.求证:BC =AD.
A
B
C
D
证明:∵ AC⊥BC,BD⊥AD ,
∴ ∠C =∠D =90°.
在Rt△ABC 和 Rt△BAD 中,
AB =BA,
AC =BD,
∴ Rt△ABC ≌ Rt△BAD(HL).
∴ BC =AD(全等三角形对应边相等).
变式. 如图,AC⊥BC,BD⊥AD,要证△ABC ≌△BAD,
需要添加一个什么条件?请说明理由.
A
B
C
D
(1)AD = BC 理由:HL
(2)AC = BD 理由:HL
(3)∠DBA = ∠CAB 理由:AAS
(4)∠DAB = ∠CBA 理由:AAS
例 如图,C 是路段AB 的中点,两人从C 同时出发,
以相同的速度分别沿两条直线行走,并同时到达D,E两地.DA⊥AB,EB⊥AB. D,E 与路段AB的距离相等吗?
为什么?
A
B
C
D
E
分析:CA=CB
CD=CE
∠A=∠B=90°
?
?
解:D,E与线段AB的距离相等.
理由:∵C是路段AB的中点,
∴AC=BC.
∵DA⊥AB , EB⊥AB ,
∴∠A=∠B=90°.
CD=CE,
AC=CB,
在Rt△ADC 和Rt△BEC 中,
∴ Rt△ADC ≌ Rt△BEC (HL).
∴ AD =BE.
∴ D,E与线段AB的距离相等.
例 如图,AB =CD,AE⊥BC,DF⊥BC,垂足分别为E ,F,CE =BF.求证:(1)AE =DF ; (2)CD//AB.
A
B
C
D
E
F
分析: CE-EF=BF-EF,即CF=BE
Rt△ABE ≌ Rt△DCF(HL)
AE=DF
∠B=∠C
CD//AB
证明:∵CE=BF,
∵AE⊥BC , DF⊥BC ,
∴∠AEB=∠DFC=90°.
AB=DC,
CF=BE,
在Rt△ABE 和Rt△DCF 中,
∴ Rt△ABE ≌ Rt△DCF (HL).
∴ AE=DF , ∠B=∠C.
∴ CD//AB.
∴CE-EF=BF-EF,即CF=BE.
例 如图,已知AB=AC,AE=AF, AE⊥EC,AF⊥BF,
垂足分别是点E、F.求证:∠1=∠2.
A
B
C
E
F
1
2
分析: Rt△AEC ≌ Rt△AFB(HL)
∠EAC=∠BAF
∠1=∠2
证明:∵ AE⊥EC,AF⊥BF ,
∴ ∠E=∠F=90°.
在Rt△AEC 和 Rt△AFB 中,
AC =AB,
AE =AF,
∴ Rt△AEC ≌ Rt△AFB(HL).
∴ ∠EAC=∠FAB(全等三角形对应角相等).
∴ ∠EAC-∠BAC=∠FAB-∠BAC.
∴∠1=∠2.
A
B
C
E
F
1
2
变式. 在上题的基础上,设EC与AB交于点M,BF与AC交于
点N,那么EM和FN相等吗?请说明理由.
M
N
?
?
解:EM=FN.
理由:在Rt△AEM 与Rt△AFN中,
∴Rt△AEM ≌Rt△AFN(ASA).
∴ EM=FN(全等三角形的对应边相等).
∠1 =∠2,
AE=AF,
∠E =∠ F=90o ,
A
B
C
E
F
1
2
M
N
课堂小结
课堂小结 判定两个直角三角形全等有哪些方法?
SSS、SAS、ASA、AAS、HL
由于已有直角条件,我们多使用后4个有角的条件的判定方法.
课堂小结 “HL”判定方法应满足什么条件?
与之前所学的四种判定方法有什么不同?
“HL”判定方法:
斜边和一条直角边分别相等的两个直角三角形全等.
此判定方法只适用于直角三角形,而之前所学的判定适用于任意三角形.
课堂小结 “HL”判定方法应满足什么条件?
与之前所学的四种判定方法有什么不同?
“HL”判定方法:
斜边和一条直角边分别相等的两个直角三角形全等.
此判定方法在直角三角形的前提下,只需满足两条边(斜边与一直角边)相等即可;之前的判定方法都需满足三个条件.
课后作业 1.如图,在△ABC中,AB=AC,AD是高.
求证:(1)BD=CD;(2)∠BAD=∠CAD.
课后作业 2.用三角板可按下面方法画角平分线:在已知∠AOB的两边上,分别取OM=ON(如图),再分别过点M、
N作OA、OB的垂线,交点为P,画射线OP,则OP平分
∠AOB,请你说出其中的道理.
同学们,再见!
问题 如图,舞台背景的形状是两个直角三角形, 为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.你能帮工作人员想个办法吗?
分析:已知一组相等的直角,还需添加什么条件,才能判定全等呢?
(1)如果用直尺和量角器两种工具,你能解决这个问题吗?
测量任意一组对应角以及
未被遮挡的任意一组对应边长度.
ASA、AAS
(2)如果只用直尺,你能解决这个问题吗?
测量未被遮挡的直角边以及斜边
如果两个直角三角形的一条直角边和斜边分别相等,这两个直角三角形全等吗?
操作 任意画一个Rt△ABC,使∠C =90°,再画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,A′B′=AB,然后把画好的Rt△A′B′C′剪下来放到Rt△ABC上,你发现了什么?
A
B
C
现象:两个三角形放在一起能完全重合.
说明:这两个三角形全等.
条件:∠C=∠C′=90°,B′C′=BC,A′B′=AB
“HL”判定方法:
斜边和一条直角边分别相等的两个直角三角形全等
(简写为“斜边、直角边”或“HL”).
N
M
C′
A
B
C
A′
B′
用符号语言表达:
在Rt△ABC 与 Rt△ A′B′C′中,
∴ Rt△ABC ≌Rt△A′B′C′ (HL).
AB =A′B′,
BC =B′C′,
∵
N
M
C′
A
B
C
A′
B′
例 如图,AC⊥BC,BD⊥AD,AC =BD.求证:BC =AD.
A
B
C
D
证明:∵ AC⊥BC,BD⊥AD ,
∴ ∠C =∠D =90°.
在Rt△ABC 和 Rt△BAD 中,
AB =BA,
AC =BD,
∴ Rt△ABC ≌ Rt△BAD(HL).
∴ BC =AD(全等三角形对应边相等).
变式. 如图,AC⊥BC,BD⊥AD,要证△ABC ≌△BAD,
需要添加一个什么条件?请说明理由.
A
B
C
D
(1)AD = BC 理由:HL
(2)AC = BD 理由:HL
(3)∠DBA = ∠CAB 理由:AAS
(4)∠DAB = ∠CBA 理由:AAS
例 如图,C 是路段AB 的中点,两人从C 同时出发,
以相同的速度分别沿两条直线行走,并同时到达D,E两地.DA⊥AB,EB⊥AB. D,E 与路段AB的距离相等吗?
为什么?
A
B
C
D
E
分析:CA=CB
CD=CE
∠A=∠B=90°
?
?
解:D,E与线段AB的距离相等.
理由:∵C是路段AB的中点,
∴AC=BC.
∵DA⊥AB , EB⊥AB ,
∴∠A=∠B=90°.
CD=CE,
AC=CB,
在Rt△ADC 和Rt△BEC 中,
∴ Rt△ADC ≌ Rt△BEC (HL).
∴ AD =BE.
∴ D,E与线段AB的距离相等.
例 如图,AB =CD,AE⊥BC,DF⊥BC,垂足分别为E ,F,CE =BF.求证:(1)AE =DF ; (2)CD//AB.
A
B
C
D
E
F
分析: CE-EF=BF-EF,即CF=BE
Rt△ABE ≌ Rt△DCF(HL)
AE=DF
∠B=∠C
CD//AB
证明:∵CE=BF,
∵AE⊥BC , DF⊥BC ,
∴∠AEB=∠DFC=90°.
AB=DC,
CF=BE,
在Rt△ABE 和Rt△DCF 中,
∴ Rt△ABE ≌ Rt△DCF (HL).
∴ AE=DF , ∠B=∠C.
∴ CD//AB.
∴CE-EF=BF-EF,即CF=BE.
例 如图,已知AB=AC,AE=AF, AE⊥EC,AF⊥BF,
垂足分别是点E、F.求证:∠1=∠2.
A
B
C
E
F
1
2
分析: Rt△AEC ≌ Rt△AFB(HL)
∠EAC=∠BAF
∠1=∠2
证明:∵ AE⊥EC,AF⊥BF ,
∴ ∠E=∠F=90°.
在Rt△AEC 和 Rt△AFB 中,
AC =AB,
AE =AF,
∴ Rt△AEC ≌ Rt△AFB(HL).
∴ ∠EAC=∠FAB(全等三角形对应角相等).
∴ ∠EAC-∠BAC=∠FAB-∠BAC.
∴∠1=∠2.
A
B
C
E
F
1
2
变式. 在上题的基础上,设EC与AB交于点M,BF与AC交于
点N,那么EM和FN相等吗?请说明理由.
M
N
?
?
解:EM=FN.
理由:在Rt△AEM 与Rt△AFN中,
∴Rt△AEM ≌Rt△AFN(ASA).
∴ EM=FN(全等三角形的对应边相等).
∠1 =∠2,
AE=AF,
∠E =∠ F=90o ,
A
B
C
E
F
1
2
M
N
课堂小结
课堂小结 判定两个直角三角形全等有哪些方法?
SSS、SAS、ASA、AAS、HL
由于已有直角条件,我们多使用后4个有角的条件的判定方法.
课堂小结 “HL”判定方法应满足什么条件?
与之前所学的四种判定方法有什么不同?
“HL”判定方法:
斜边和一条直角边分别相等的两个直角三角形全等.
此判定方法只适用于直角三角形,而之前所学的判定适用于任意三角形.
课堂小结 “HL”判定方法应满足什么条件?
与之前所学的四种判定方法有什么不同?
“HL”判定方法:
斜边和一条直角边分别相等的两个直角三角形全等.
此判定方法在直角三角形的前提下,只需满足两条边(斜边与一直角边)相等即可;之前的判定方法都需满足三个条件.
课后作业 1.如图,在△ABC中,AB=AC,AD是高.
求证:(1)BD=CD;(2)∠BAD=∠CAD.
课后作业 2.用三角板可按下面方法画角平分线:在已知∠AOB的两边上,分别取OM=ON(如图),再分别过点M、
N作OA、OB的垂线,交点为P,画射线OP,则OP平分
∠AOB,请你说出其中的道理.
同学们,再见!
