人教版八年级上册12.3角的平分线的性质(第三课时)课件(24张)
文档属性
| 名称 | 人教版八年级上册12.3角的平分线的性质(第三课时)课件(24张) |  | |
| 格式 | pptx | ||
| 文件大小 | 346.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:08:24 | ||
图片预览


文档简介
角的平分线的性质(第三课时)
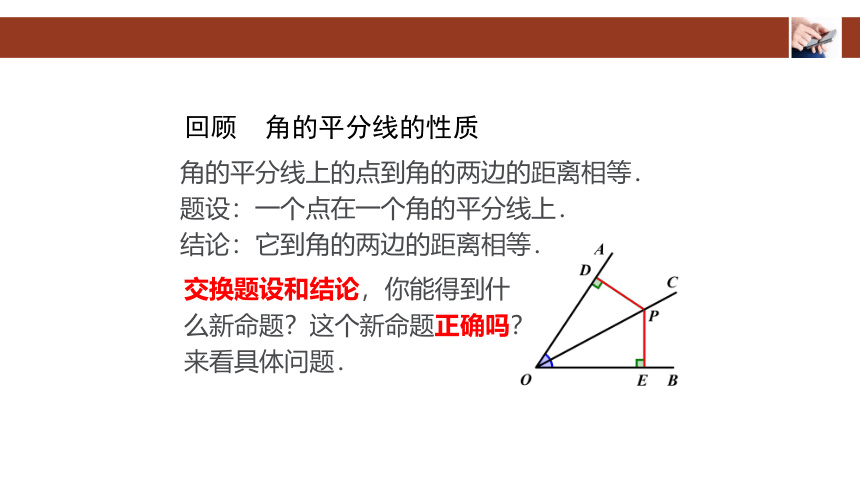
回顾 角的平分线的性质
角的平分线上的点到角的两边的距离相等.
题设:一个点在一个角的平分线上.
结论:它到角的两边的距离相等.
交换题设和结论,你能得到什么新命题?这个新命题正确吗?
来看具体问题.
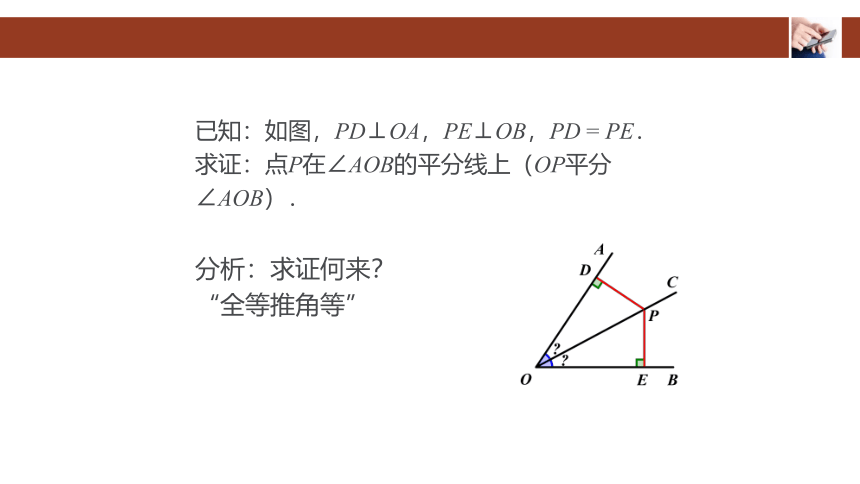
已知:如图,PD⊥OA,PE⊥OB,PD = PE.
求证:点P在∠AOB的平分线上(OP平分∠AOB).
分析:求证何来?
“全等推角等”
∵ PD⊥OA,PE⊥OB(已知),
∴ ∠PDO = ∠PEO = 90°.
在Rt△PDO和Rt△PEO中,
?
∴ Rt△PDO≌Rt△PEO(HL).
∴ ∠POD = ∠POE.即点P
在∠AOB的平分线上.
证明:
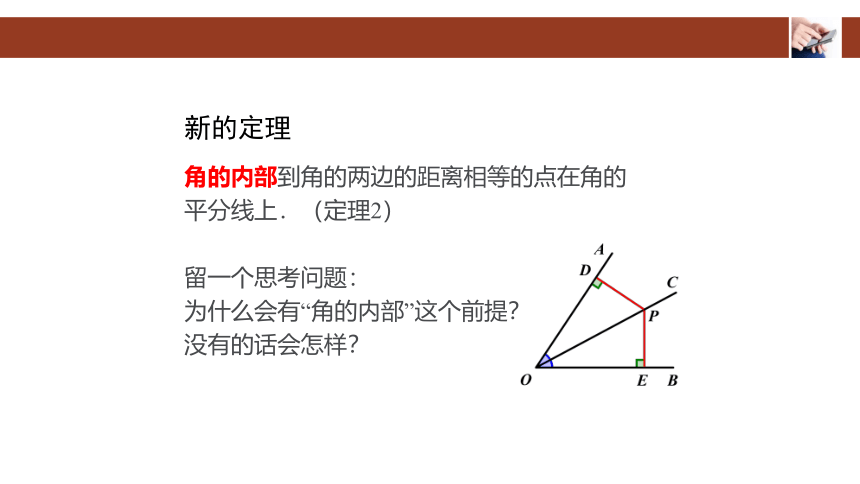
新的定理
角的内部到角的两边的距离相等的点在角的
平分线上.(定理2)
留一个思考问题:
为什么会有“角的内部”这个前提?
没有的话会怎样?
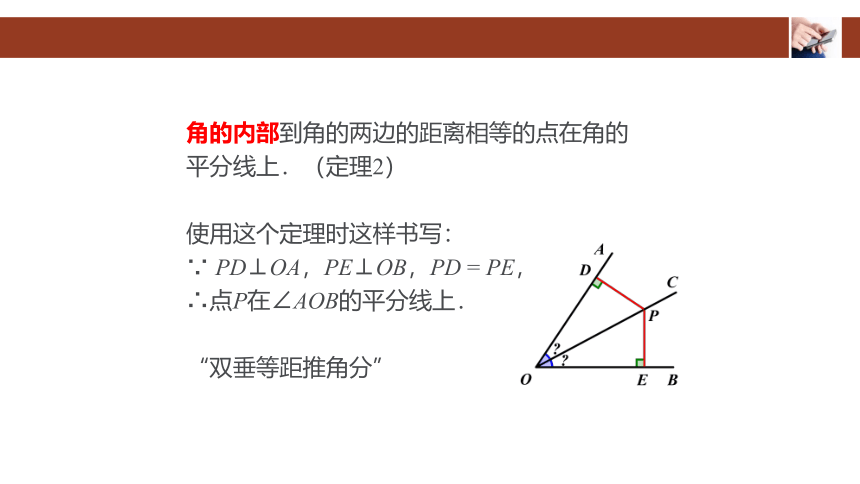
角的内部到角的两边的距离相等的点在角的
平分线上.(定理2)
使用这个定理时这样书写:
∵ PD⊥OA,PE⊥OB,PD = PE,
∴点P在∠AOB的平分线上.
“双垂等距推角分”
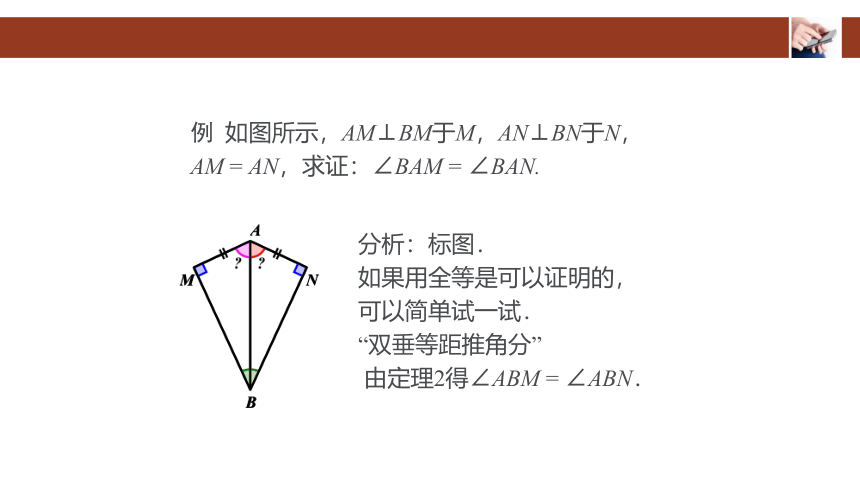
例 如图所示,AM⊥BM于M,AN⊥BN于N,
AM = AN,求证:∠BAM = ∠BAN.
分析:标图.
如果用全等是可以证明的,
可以简单试一试.
“双垂等距推角分”
由定理2得∠ABM = ∠ABN.
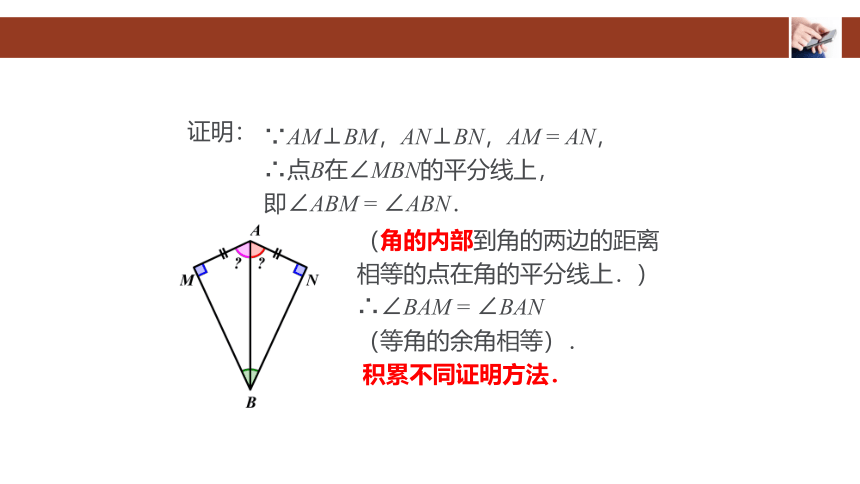
∵AM⊥BM,AN⊥BN,AM = AN,
∴点B在∠MBN的平分线上,
即∠ABM = ∠ABN.
(角的内部到角的两边的距离相等的点在角的平分线上.)
∴∠BAM = ∠BAN
(等角的余角相等).
积累不同证明方法.
证明:
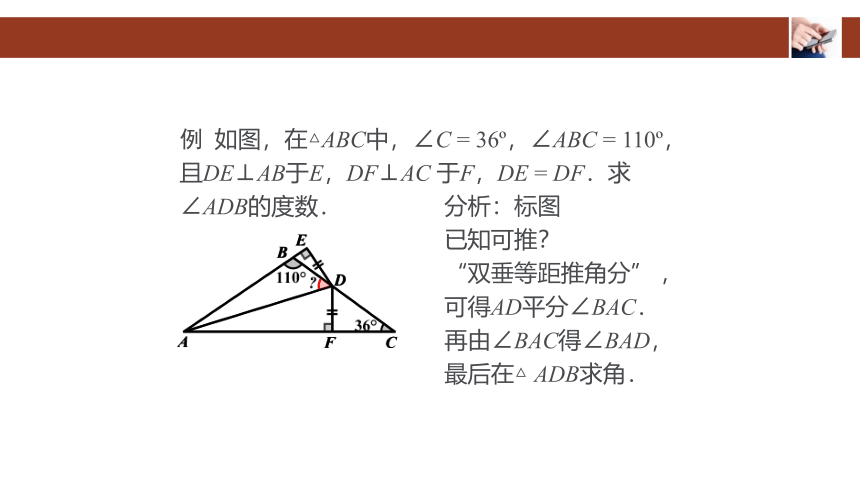
分析:标图
已知可推?
“双垂等距推角分” ,可得AD平分∠BAC.
再由∠BAC得∠BAD,
最后在△ ADB求角.
例 如图,在△ABC中,∠C = 36?,∠ABC = 110?,且DE⊥AB于E,DF⊥AC 于F,DE = DF.求∠ADB的度数.
∵∠C = 36?,∠ABC = 110?,
∴∠BAC = 180?﹣36?﹣110? = 34? .
∵DE⊥AB于E,DF⊥AC 于
F,DE = DF,
∴AD平分∠BAC .
∴∠BAD = 17? .
∴∠ADB = 180?﹣110?﹣17?
= 53?.
解:
基本图不变
例 如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB = OC,连AO,求证:∠1 = ∠2.
分析:标图
已知可推?
△ODB≌△OEC
求证何来?
全等?定理2更好
需要OD = OE
∵CD⊥AB,BE⊥AC,
∴∠BDO = ∠CEO = 90°.
?在△ODB和△OEC中
∴△ODB≌△OEC.
∴OD = OE.
又OD⊥AB,OE⊥AC,
∴点O在∠BOC的平分
线上,即∠1 = ∠2.
证明:
例 如图,D,E,F分别是△ABC的三条边上的点,BE = CF,△DBE和△DCF的面积相等.求证:AD平分∠BAC.
分析:标图
已知可推?
直接用面积要找底高
考虑作垂直
面积和一边等,则高等
“双垂等距推角分”
求证何来?
例 BE = CF,△DBE和△DCF的面积相等.求证:AD平分∠BAC.
证明:过D作DM⊥AB于M,DN⊥AC于N.
∵△DBE和△DCF的面积相等,
∴ BE?DM = CF?DN.
又∵BE = CF,
又∵DM⊥AB,DN⊥AC,
∴AD平分∠BAC
∴DM = DN.
辅助线不变
分析:标图
已知可推?邻补角好找180?
可以转换为等角的条件
求证何来?
“双垂等距推角分”
作双垂,欠等距,
全等推
例 如图,OP为∠AOB内一条射线,C,D分别为OA,OB上两点,且∠PCO+∠PDO = 180?,PC = PD.求证:OP平分∠AOB.
例 如图,OP为∠AOB内一条射线,C,D分别为OA,OB上两点,且∠PCO+∠PDO = 180?,PC = PD.求证:OP平分∠AOB.
整理一下思路:
1.作双垂
2.由180?找等角,供全等用
3.证明两三角形全等
4.得距离等,配双垂证角等
证明:过点P作PM⊥OA,PN⊥OB.
则∠PMC = ∠PND = 90? .
∵∠PCO+∠PDO = 180?,∠PCO+∠PCM = 180? ,
∴∠PCM = ∠PDN.
在△PMC与△PND中
∴△PMC≌△PND.
∴PM = PN.
又∵PM⊥OA,
PN⊥OB,
∴OP平分∠AOB.
3 新的关注
两个定理的异同(基本图,辅助线相同).
今天研究的内容
2 新的应用
“双垂等距推角分” .
1 新的定理
角的内部到角的两边的距离相等的点在
角的平分线上.
1.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以
作出一个角的平分线.如图:一把直尺
压住射线OB,另一把直尺压住射线OA
并且与第一把直尺交于点P,小明说:
“射线OP就是∠BOA的角平分线.”
他这样做的依据是( ).
作业
1.小明同学在学习了全等三角形的相关知识后发现,A.角的内部到角的两边的距离
相等的点在角的平分线上
B.角平分线上的点到这个角两边的
距离相等
C.三角形三条角平分线的交点
到三条边的距离相等
D.以上均不正确
作业
作业
2.如图所示,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是点E,F,且
BE = CF,求证:AD是△ABC的角平分线.
同学们,再见!
练习 如图,BE = CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB = DC,求证:AD是∠BAC的平分线.
分析:标图
已知可推?
全等较明显
求证何来?
定理2更好
需要DE = DF
∵DE⊥AB延长线于E,DF⊥AC于F,
∴∠BED = ∠CFD = 90°.
在Rt△BDE与Rt△CDF中,
?
∴Rt△BDE≌Rt△CDF(HL).
∴DE = DF.
∴AD是∠BAC的平分线.
证明:
①
又∵①
回顾 角的平分线的性质
角的平分线上的点到角的两边的距离相等.
题设:一个点在一个角的平分线上.
结论:它到角的两边的距离相等.
交换题设和结论,你能得到什么新命题?这个新命题正确吗?
来看具体问题.
已知:如图,PD⊥OA,PE⊥OB,PD = PE.
求证:点P在∠AOB的平分线上(OP平分∠AOB).
分析:求证何来?
“全等推角等”
∵ PD⊥OA,PE⊥OB(已知),
∴ ∠PDO = ∠PEO = 90°.
在Rt△PDO和Rt△PEO中,
?
∴ Rt△PDO≌Rt△PEO(HL).
∴ ∠POD = ∠POE.即点P
在∠AOB的平分线上.
证明:
新的定理
角的内部到角的两边的距离相等的点在角的
平分线上.(定理2)
留一个思考问题:
为什么会有“角的内部”这个前提?
没有的话会怎样?
角的内部到角的两边的距离相等的点在角的
平分线上.(定理2)
使用这个定理时这样书写:
∵ PD⊥OA,PE⊥OB,PD = PE,
∴点P在∠AOB的平分线上.
“双垂等距推角分”
例 如图所示,AM⊥BM于M,AN⊥BN于N,
AM = AN,求证:∠BAM = ∠BAN.
分析:标图.
如果用全等是可以证明的,
可以简单试一试.
“双垂等距推角分”
由定理2得∠ABM = ∠ABN.
∵AM⊥BM,AN⊥BN,AM = AN,
∴点B在∠MBN的平分线上,
即∠ABM = ∠ABN.
(角的内部到角的两边的距离相等的点在角的平分线上.)
∴∠BAM = ∠BAN
(等角的余角相等).
积累不同证明方法.
证明:
分析:标图
已知可推?
“双垂等距推角分” ,可得AD平分∠BAC.
再由∠BAC得∠BAD,
最后在△ ADB求角.
例 如图,在△ABC中,∠C = 36?,∠ABC = 110?,且DE⊥AB于E,DF⊥AC 于F,DE = DF.求∠ADB的度数.
∵∠C = 36?,∠ABC = 110?,
∴∠BAC = 180?﹣36?﹣110? = 34? .
∵DE⊥AB于E,DF⊥AC 于
F,DE = DF,
∴AD平分∠BAC .
∴∠BAD = 17? .
∴∠ADB = 180?﹣110?﹣17?
= 53?.
解:
基本图不变
例 如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB = OC,连AO,求证:∠1 = ∠2.
分析:标图
已知可推?
△ODB≌△OEC
求证何来?
全等?定理2更好
需要OD = OE
∵CD⊥AB,BE⊥AC,
∴∠BDO = ∠CEO = 90°.
?在△ODB和△OEC中
∴△ODB≌△OEC.
∴OD = OE.
又OD⊥AB,OE⊥AC,
∴点O在∠BOC的平分
线上,即∠1 = ∠2.
证明:
例 如图,D,E,F分别是△ABC的三条边上的点,BE = CF,△DBE和△DCF的面积相等.求证:AD平分∠BAC.
分析:标图
已知可推?
直接用面积要找底高
考虑作垂直
面积和一边等,则高等
“双垂等距推角分”
求证何来?
例 BE = CF,△DBE和△DCF的面积相等.求证:AD平分∠BAC.
证明:过D作DM⊥AB于M,DN⊥AC于N.
∵△DBE和△DCF的面积相等,
∴ BE?DM = CF?DN.
又∵BE = CF,
又∵DM⊥AB,DN⊥AC,
∴AD平分∠BAC
∴DM = DN.
辅助线不变
分析:标图
已知可推?邻补角好找180?
可以转换为等角的条件
求证何来?
“双垂等距推角分”
作双垂,欠等距,
全等推
例 如图,OP为∠AOB内一条射线,C,D分别为OA,OB上两点,且∠PCO+∠PDO = 180?,PC = PD.求证:OP平分∠AOB.
例 如图,OP为∠AOB内一条射线,C,D分别为OA,OB上两点,且∠PCO+∠PDO = 180?,PC = PD.求证:OP平分∠AOB.
整理一下思路:
1.作双垂
2.由180?找等角,供全等用
3.证明两三角形全等
4.得距离等,配双垂证角等
证明:过点P作PM⊥OA,PN⊥OB.
则∠PMC = ∠PND = 90? .
∵∠PCO+∠PDO = 180?,∠PCO+∠PCM = 180? ,
∴∠PCM = ∠PDN.
在△PMC与△PND中
∴△PMC≌△PND.
∴PM = PN.
又∵PM⊥OA,
PN⊥OB,
∴OP平分∠AOB.
3 新的关注
两个定理的异同(基本图,辅助线相同).
今天研究的内容
2 新的应用
“双垂等距推角分” .
1 新的定理
角的内部到角的两边的距离相等的点在
角的平分线上.
1.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以
作出一个角的平分线.如图:一把直尺
压住射线OB,另一把直尺压住射线OA
并且与第一把直尺交于点P,小明说:
“射线OP就是∠BOA的角平分线.”
他这样做的依据是( ).
作业
1.小明同学在学习了全等三角形的相关知识后发现,A.角的内部到角的两边的距离
相等的点在角的平分线上
B.角平分线上的点到这个角两边的
距离相等
C.三角形三条角平分线的交点
到三条边的距离相等
D.以上均不正确
作业
作业
2.如图所示,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是点E,F,且
BE = CF,求证:AD是△ABC的角平分线.
同学们,再见!
练习 如图,BE = CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB = DC,求证:AD是∠BAC的平分线.
分析:标图
已知可推?
全等较明显
求证何来?
定理2更好
需要DE = DF
∵DE⊥AB延长线于E,DF⊥AC于F,
∴∠BED = ∠CFD = 90°.
在Rt△BDE与Rt△CDF中,
?
∴Rt△BDE≌Rt△CDF(HL).
∴DE = DF.
∴AD是∠BAC的平分线.
证明:
①
又∵①
