人教版八年级上册13.1.2线段的垂直平分线的性质(第二课时)课件(16张)
文档属性
| 名称 | 人教版八年级上册13.1.2线段的垂直平分线的性质(第二课时)课件(16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 186.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览






文档简介
线段的垂直平分线的性质(第二课时)
{5940675A-B579-460E-94D1-54222C63F5DA}
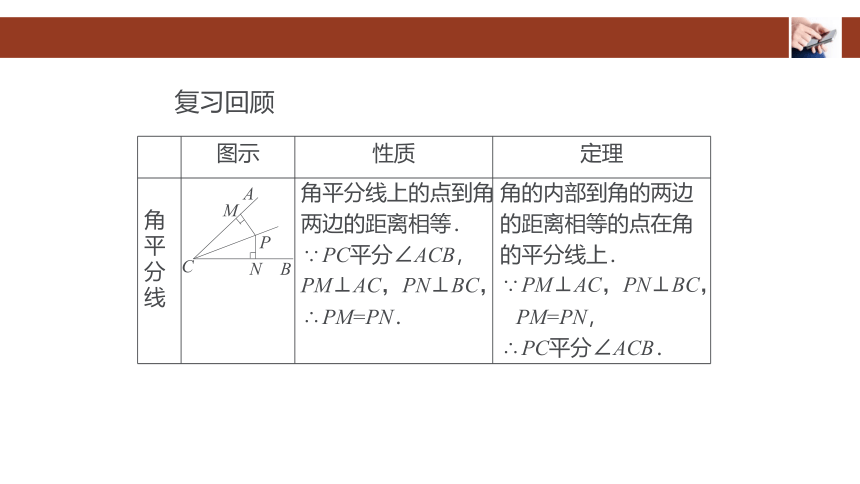
图示
性质
定理
角平分线
A
C
B
P
M
N
角平分线上的点到角两边的距离相等.
∵PC平分∠ACB,
PM⊥AC,PN⊥BC,
∴PM=PN.
角的内部到角的两边的距离相等的点在角的平分线上.
∵PM⊥AC,PN⊥BC,
PM=PN,
∴PC平分∠ACB.
复习回顾
{5940675A-B579-460E-94D1-54222C63F5DA}
图示
性质
线段的垂直平分线
A
B
l
C
P
线段垂直平分线上的点与这条线段两个端点的距离相等.
∵直线l是线段AB的垂直平分线,
∴PA=PB.
猜想
与线段两个端点距离相等的点在这条线段的垂直平分线上.
复习回顾
∵PA=PB,
∴点P在线段AB的垂直平分线上.
如图,已知PA=PB,
求证:点P在AB的垂直平分线上.
l
C
B
A
P
分析:要证点P在AB的垂直平分线上,
只需证点P和AB的中点C所连直线PC是AB的垂直平分线,即PC⊥AB.
只需证△PAC≌△PBC(SSS).
取中点,证垂直
如图,已知PA=PB,
求证:点P在AB的垂直平分线上.
l
C
B
A
P
证明:取AB中点C,作直线PC.
∴AC=CB.
∵在△PAC和△PBC中,
∵∠ACP+∠BCP=180°,
∴∠ACP=∠BCP=90°.
∴PC⊥AB.
∴PC是AB的垂直平分线,
即点P在AB的垂直平分线上.
∴△PAC≌△PBC(SSS) .
∴∠ACP=∠BCP.
【小结】
此方法可以称为“取中点,证垂直”,也可以“作垂直,证中点”,
留给同学们自主完成.
l
C
B
A
P
如图,已知PA=PB,
求证:点P在AB的垂直平分线上.
定理:与线段两个端点距离相等的点在这条线段的垂直平分线上.
例 如图,AD为∠BAC的平分线,DE ⊥AB于E,DF⊥AC于F,求证:AD是EF的垂直平分线.
分析:要证AD是EF的垂直平分线,只需证点A和点D都在EF的垂直平分线上,
也就是要证AE=AF,DE=DF.
A
B
C
D
E
F
证明:∵AD为∠BAC的平分线
∴∠DAE=∠DAF.
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
∵在△ADE和△ADF中,
∴AE=AF,DE=DF.
∴点A和点D都在EF的垂直平分线上.
∴AD是EF的垂直平分线.
∴△ADE≌△ADF(AAS).
A
B
C
D
E
F
例 如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,分别交BC于点D,E,已知△ADE的周长为5 cm.
(1)求BC的长;
(2)求证:点O在BC的垂直平分线上.
解:(1)∵AB的垂直平分线是OM,
AC的垂直平分线是ON,
∴AD=BD,AE=CE.
∵△ADE的周长为AD+DE+AE=5 cm,
∴BC=BD+DE+CE=AD+DE+AE=5 cm.
证明:(2)连接OA,OB,OC,
∵AB的垂直平分线是OM,
AC的垂直平分线是ON,
∴OA=OB,OA=OC.
∴OB=OC.
∴点O在BC的垂直平分线上.
例 如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,分别交BC于点D,E,已知△ADE的周长为5 cm.
(1)求BC的长;
(2)求证:点O在BC的垂直平分线上.
小结:
(1)常见的辅助线:连接要证的垂直平分线上的点到线段两端点的距离;
(2)三角形三边的垂直平分线交于一点.
定理:
与线段两个端点距离相等的点在这条线段的垂直平分线上.
A
B
P
l
C
A
B
P
l
C
课堂小结
1. 如图,AD与BC相交于点O,OA=OC,∠A=∠C,BE=DE.
求证:OE垂直平分BD.
作 业
2. 下面小东设计的“作三角形一边上的高”的尺规作图过程.
?已知:△ABC.
求作:△ABC的边BC上的高AD.
?
作法:如图,
(1)分别以点B和点C为圆心,BA,CA为半径作弧,两弧相交于点E;
(2)作直线AE交BC边于点D.
所以线段AD就是所求作的高.
A
B
C
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵AB=_______,AC=_______,
∴点B,C都在线段AE的垂直平分线上
( )(填推理的依据).
∴直线BC是线段AE的垂直平分线
( )(填推理的依据).
∴AD⊥BC,即AD是△ABC的边BC上的高.
同学们,再见!
{5940675A-B579-460E-94D1-54222C63F5DA}
图示
性质
定理
角平分线
A
C
B
P
M
N
角平分线上的点到角两边的距离相等.
∵PC平分∠ACB,
PM⊥AC,PN⊥BC,
∴PM=PN.
角的内部到角的两边的距离相等的点在角的平分线上.
∵PM⊥AC,PN⊥BC,
PM=PN,
∴PC平分∠ACB.
复习回顾
{5940675A-B579-460E-94D1-54222C63F5DA}
图示
性质
线段的垂直平分线
A
B
l
C
P
线段垂直平分线上的点与这条线段两个端点的距离相等.
∵直线l是线段AB的垂直平分线,
∴PA=PB.
猜想
与线段两个端点距离相等的点在这条线段的垂直平分线上.
复习回顾
∵PA=PB,
∴点P在线段AB的垂直平分线上.
如图,已知PA=PB,
求证:点P在AB的垂直平分线上.
l
C
B
A
P
分析:要证点P在AB的垂直平分线上,
只需证点P和AB的中点C所连直线PC是AB的垂直平分线,即PC⊥AB.
只需证△PAC≌△PBC(SSS).
取中点,证垂直
如图,已知PA=PB,
求证:点P在AB的垂直平分线上.
l
C
B
A
P
证明:取AB中点C,作直线PC.
∴AC=CB.
∵在△PAC和△PBC中,
∵∠ACP+∠BCP=180°,
∴∠ACP=∠BCP=90°.
∴PC⊥AB.
∴PC是AB的垂直平分线,
即点P在AB的垂直平分线上.
∴△PAC≌△PBC(SSS) .
∴∠ACP=∠BCP.
【小结】
此方法可以称为“取中点,证垂直”,也可以“作垂直,证中点”,
留给同学们自主完成.
l
C
B
A
P
如图,已知PA=PB,
求证:点P在AB的垂直平分线上.
定理:与线段两个端点距离相等的点在这条线段的垂直平分线上.
例 如图,AD为∠BAC的平分线,DE ⊥AB于E,DF⊥AC于F,求证:AD是EF的垂直平分线.
分析:要证AD是EF的垂直平分线,只需证点A和点D都在EF的垂直平分线上,
也就是要证AE=AF,DE=DF.
A
B
C
D
E
F
证明:∵AD为∠BAC的平分线
∴∠DAE=∠DAF.
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
∵在△ADE和△ADF中,
∴AE=AF,DE=DF.
∴点A和点D都在EF的垂直平分线上.
∴AD是EF的垂直平分线.
∴△ADE≌△ADF(AAS).
A
B
C
D
E
F
例 如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,分别交BC于点D,E,已知△ADE的周长为5 cm.
(1)求BC的长;
(2)求证:点O在BC的垂直平分线上.
解:(1)∵AB的垂直平分线是OM,
AC的垂直平分线是ON,
∴AD=BD,AE=CE.
∵△ADE的周长为AD+DE+AE=5 cm,
∴BC=BD+DE+CE=AD+DE+AE=5 cm.
证明:(2)连接OA,OB,OC,
∵AB的垂直平分线是OM,
AC的垂直平分线是ON,
∴OA=OB,OA=OC.
∴OB=OC.
∴点O在BC的垂直平分线上.
例 如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,分别交BC于点D,E,已知△ADE的周长为5 cm.
(1)求BC的长;
(2)求证:点O在BC的垂直平分线上.
小结:
(1)常见的辅助线:连接要证的垂直平分线上的点到线段两端点的距离;
(2)三角形三边的垂直平分线交于一点.
定理:
与线段两个端点距离相等的点在这条线段的垂直平分线上.
A
B
P
l
C
A
B
P
l
C
课堂小结
1. 如图,AD与BC相交于点O,OA=OC,∠A=∠C,BE=DE.
求证:OE垂直平分BD.
作 业
2. 下面小东设计的“作三角形一边上的高”的尺规作图过程.
?已知:△ABC.
求作:△ABC的边BC上的高AD.
?
作法:如图,
(1)分别以点B和点C为圆心,BA,CA为半径作弧,两弧相交于点E;
(2)作直线AE交BC边于点D.
所以线段AD就是所求作的高.
A
B
C
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵AB=_______,AC=_______,
∴点B,C都在线段AE的垂直平分线上
( )(填推理的依据).
∴直线BC是线段AE的垂直平分线
( )(填推理的依据).
∴AD⊥BC,即AD是△ABC的边BC上的高.
同学们,再见!
