人教版八年级上册13.1.2线段的垂直平分线的性质(第三课时)课件(20张)
文档属性
| 名称 | 人教版八年级上册13.1.2线段的垂直平分线的性质(第三课时)课件(20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 225.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:08:58 | ||
图片预览



文档简介
线段的垂直平分线的性质(第三课时)
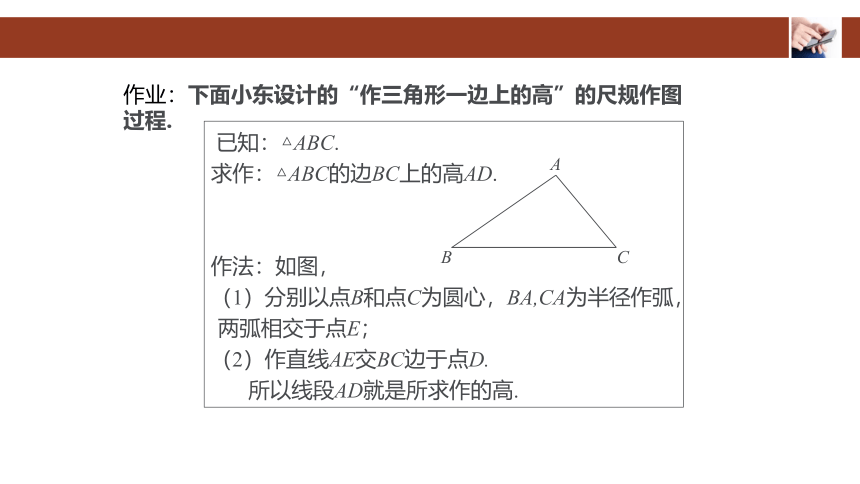
作业:下面小东设计的“作三角形一边上的高”的尺规作图过程.
?已知:△ABC.
求作:△ABC的边BC上的高AD.
?
作法:如图,
(1)分别以点B和点C为圆心,BA,CA为半径作弧,两弧相交于点E;
(2)作直线AE交BC边于点D.
所以线段AD就是所求作的高.
A
B
C
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
作法:如图,
(1)分别以点B和点C为圆心,BA,
CA为半径作弧,两弧相交于点E;
(2)作直线AE交BC边于点D.
所以线段AD就是所求作的高.
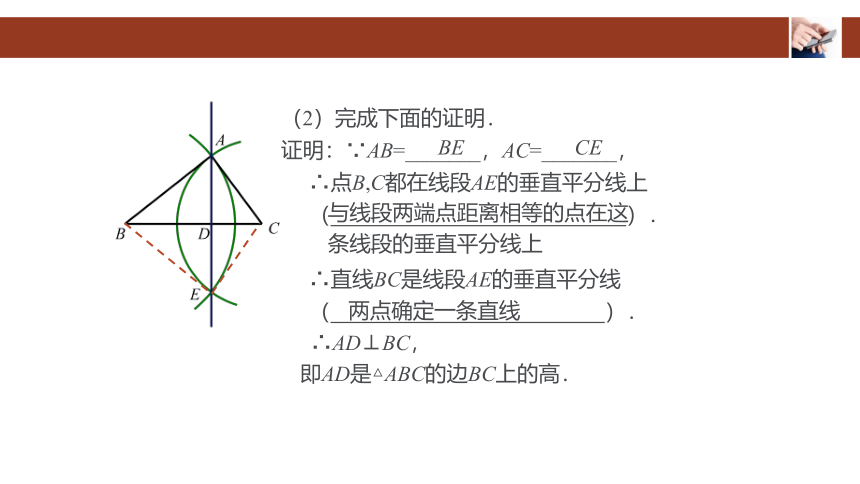
(2)完成下面的证明.
证明:∵AB=_______,AC=_______,
∴点B,C都在线段AE的垂直平分线上
( ).
∴直线BC是线段AE的垂直平分线
( ).
∴AD⊥BC,
即AD是△ABC的边BC上的高.
BE
CE
与线段两端点距离相等的点在这条线段的垂直平分线上
两点确定一条直线
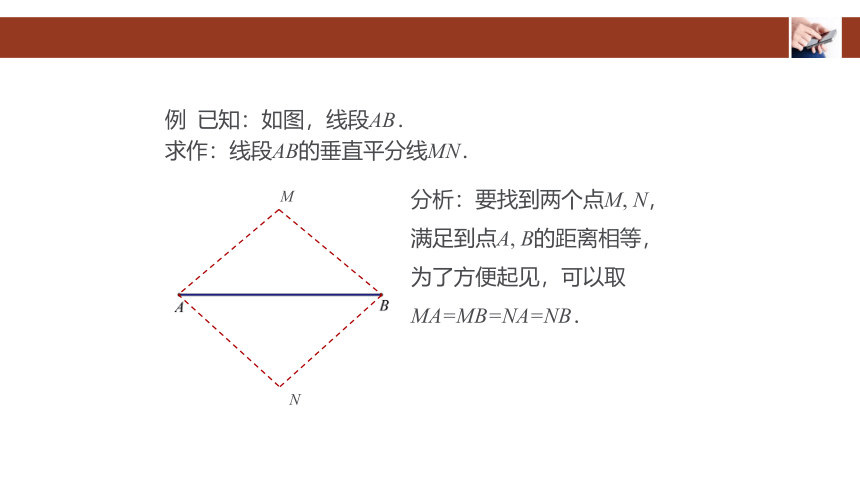
例 已知:如图,线段AB.
求作:线段AB的垂直平分线MN.
分析:要找到两个点M, N,
满足到点A, B的距离相等,
为了方便起见,可以取
MA=MB=NA=NB.
M
N
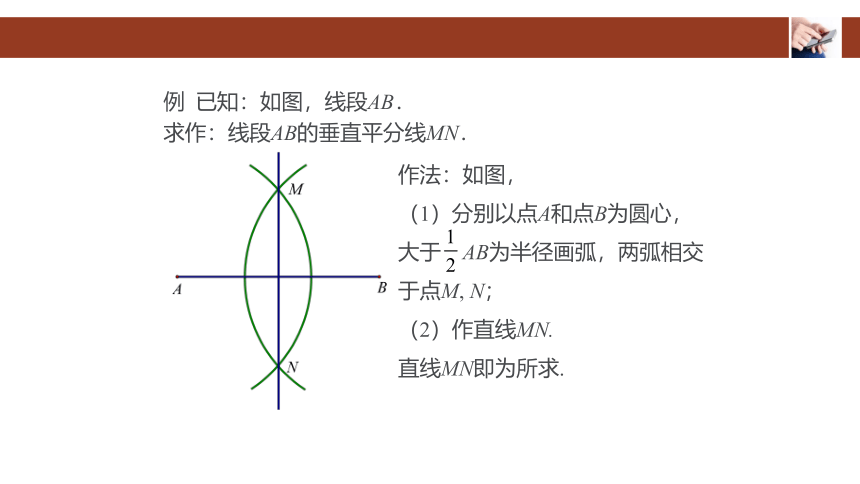
例 已知:如图,线段AB.
求作:线段AB的垂直平分线MN.
作法:如图,
(1)分别以点A和点B为圆心,
大于 AB为半径画弧,两弧相交于点M, N;
(2)作直线MN.
直线MN即为所求.
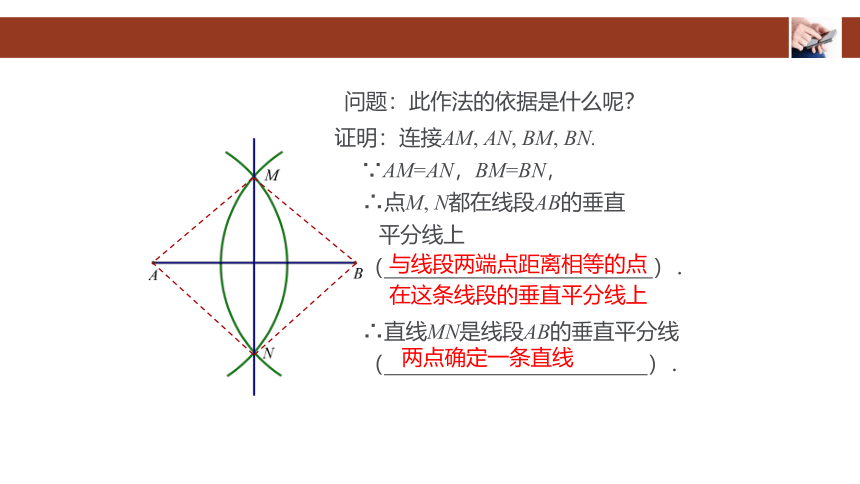
问题:此作法的依据是什么呢?
证明:连接AM, AN, BM, BN.
∵AM=AN,BM=BN,
∴点M, N都在线段AB的垂直
平分线上
( ).
∴直线MN是线段AB的垂直平分线
( ).
与线段两端点距离相等的点
在这条线段的垂直平分线上
两点确定一条直线
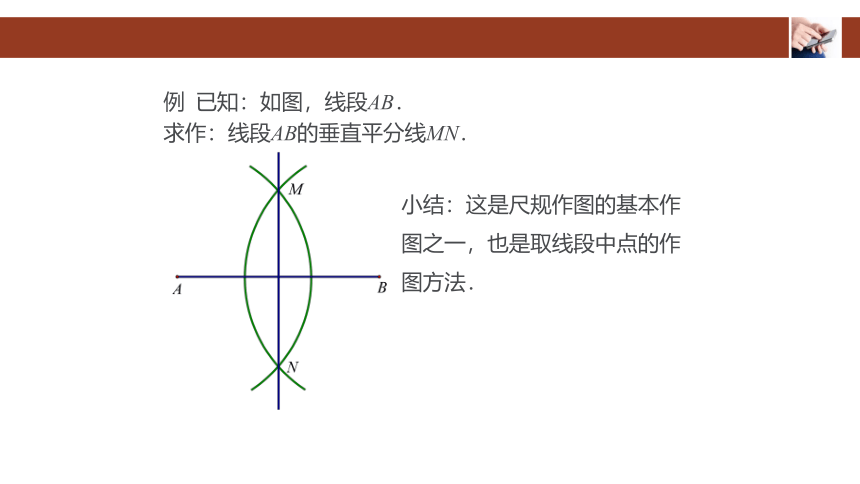
例 已知:如图,线段AB.
求作:线段AB的垂直平分线MN.
小结:这是尺规作图的基本作图之一,也是取线段中点的作图方法.
已知:直线AB和AB外一点P,
求作:AB的垂线,使它经过点P.
分析:在直线AB上构造线段DE,
使得点P在线段DE的垂直平分线上.
则需满足PD=PE .
(3)分别以点D和点E为圆心,大于 DE的长为半径作弧,两弧相交于点F.
作法:(1)任意取一点K,使点K和点P在AB的两旁.
(2)以点P为圆心,PK长为半径作弧,交AB于点D和E.
(4)作直线PF.
直线PF就是所求作的垂线.
已知:直线AB和AB上一点P,
求作:AB的垂线,使它经过点P.
分析:在直线AB上构造线段DE,
使得点P在线段DE的垂直平分线上.
则需满足PD=PE .
小结:尺规作图的5种基本作图
①作一条线段等于已知线段;
②作已知线段的垂直平分线(中点);
③作已知角的角平分线;
④作一个角等于已知角;
⑤过一点作已知直线的垂线.
之后都是利用基本作图来作图,不要求写作法.
例 作出下列图形的一条对称轴.
(1)
A
B
l
找到一对对称点A,B,连接AB,
作出线段AB的垂直平分线l,
则l就是这个五角星的对称轴.
例 作出下列图形的一条对称轴.
(2)
A
B
A
B
例 如图,A,B,C三点表示三个村庄,为了解决村民子女就近入学问题,计划新建一所学校P,要使学校P到三个村庄的距离相等,请你利用尺规作图确定学校的位置.
分析:
点P到点A,B的距离相等,即PA=PB,
则点P在线段AB的垂直平分线上;
点P到点A,C的距离相等,即PA=PC,
则点P在线段AC的垂直平分线上.
例 如图,A,B,C三点表示三个村庄,为了解决村民子女就近入学问题,计划新建一所学校P,要使学校P到三个村庄的距离相等,请你利用尺规作图确定学校的位置.
作法:分别作线段AB和AC的垂直平分线,两条直线相交于点P,
∴点P即为所求.
本节课学习了尺规作图的两种基本作图,并利用它来解决简单的作图问题.
课堂小结
1. 如图所示的虚线中,哪些是图形的对称轴?
作 业
整理笔记,将本节课涉及的尺规作图再画一遍.
2. 如图,某地由于居民增多,要在公路l上增加一个公共汽车站,A,B是路边两个新建小区,请你利用尺规作图确定这个公共汽车站建在什么位置,能使两个小区到车站的路程一样长?
A
B
l
同学们,再见!
作业:下面小东设计的“作三角形一边上的高”的尺规作图过程.
?已知:△ABC.
求作:△ABC的边BC上的高AD.
?
作法:如图,
(1)分别以点B和点C为圆心,BA,CA为半径作弧,两弧相交于点E;
(2)作直线AE交BC边于点D.
所以线段AD就是所求作的高.
A
B
C
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
作法:如图,
(1)分别以点B和点C为圆心,BA,
CA为半径作弧,两弧相交于点E;
(2)作直线AE交BC边于点D.
所以线段AD就是所求作的高.
(2)完成下面的证明.
证明:∵AB=_______,AC=_______,
∴点B,C都在线段AE的垂直平分线上
( ).
∴直线BC是线段AE的垂直平分线
( ).
∴AD⊥BC,
即AD是△ABC的边BC上的高.
BE
CE
与线段两端点距离相等的点在这条线段的垂直平分线上
两点确定一条直线
例 已知:如图,线段AB.
求作:线段AB的垂直平分线MN.
分析:要找到两个点M, N,
满足到点A, B的距离相等,
为了方便起见,可以取
MA=MB=NA=NB.
M
N
例 已知:如图,线段AB.
求作:线段AB的垂直平分线MN.
作法:如图,
(1)分别以点A和点B为圆心,
大于 AB为半径画弧,两弧相交于点M, N;
(2)作直线MN.
直线MN即为所求.
问题:此作法的依据是什么呢?
证明:连接AM, AN, BM, BN.
∵AM=AN,BM=BN,
∴点M, N都在线段AB的垂直
平分线上
( ).
∴直线MN是线段AB的垂直平分线
( ).
与线段两端点距离相等的点
在这条线段的垂直平分线上
两点确定一条直线
例 已知:如图,线段AB.
求作:线段AB的垂直平分线MN.
小结:这是尺规作图的基本作图之一,也是取线段中点的作图方法.
已知:直线AB和AB外一点P,
求作:AB的垂线,使它经过点P.
分析:在直线AB上构造线段DE,
使得点P在线段DE的垂直平分线上.
则需满足PD=PE .
(3)分别以点D和点E为圆心,大于 DE的长为半径作弧,两弧相交于点F.
作法:(1)任意取一点K,使点K和点P在AB的两旁.
(2)以点P为圆心,PK长为半径作弧,交AB于点D和E.
(4)作直线PF.
直线PF就是所求作的垂线.
已知:直线AB和AB上一点P,
求作:AB的垂线,使它经过点P.
分析:在直线AB上构造线段DE,
使得点P在线段DE的垂直平分线上.
则需满足PD=PE .
小结:尺规作图的5种基本作图
①作一条线段等于已知线段;
②作已知线段的垂直平分线(中点);
③作已知角的角平分线;
④作一个角等于已知角;
⑤过一点作已知直线的垂线.
之后都是利用基本作图来作图,不要求写作法.
例 作出下列图形的一条对称轴.
(1)
A
B
l
找到一对对称点A,B,连接AB,
作出线段AB的垂直平分线l,
则l就是这个五角星的对称轴.
例 作出下列图形的一条对称轴.
(2)
A
B
A
B
例 如图,A,B,C三点表示三个村庄,为了解决村民子女就近入学问题,计划新建一所学校P,要使学校P到三个村庄的距离相等,请你利用尺规作图确定学校的位置.
分析:
点P到点A,B的距离相等,即PA=PB,
则点P在线段AB的垂直平分线上;
点P到点A,C的距离相等,即PA=PC,
则点P在线段AC的垂直平分线上.
例 如图,A,B,C三点表示三个村庄,为了解决村民子女就近入学问题,计划新建一所学校P,要使学校P到三个村庄的距离相等,请你利用尺规作图确定学校的位置.
作法:分别作线段AB和AC的垂直平分线,两条直线相交于点P,
∴点P即为所求.
本节课学习了尺规作图的两种基本作图,并利用它来解决简单的作图问题.
课堂小结
1. 如图所示的虚线中,哪些是图形的对称轴?
作 业
整理笔记,将本节课涉及的尺规作图再画一遍.
2. 如图,某地由于居民增多,要在公路l上增加一个公共汽车站,A,B是路边两个新建小区,请你利用尺规作图确定这个公共汽车站建在什么位置,能使两个小区到车站的路程一样长?
A
B
l
同学们,再见!
