人教版八年级上册13.2画轴对称图形课件(33张)
文档属性
| 名称 | 人教版八年级上册13.2画轴对称图形课件(33张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 16:15:52 | ||
图片预览






文档简介
画轴对称图形
复习回顾
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称.这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.
复习回顾
性质 :
1. 如果两个图形关于某直线成轴对称,
那么这两个图形全等.
2. 如果两个图形关于某条直线成轴对称,
那么对称轴是任何一对对应点所连
线段的垂直平分线.
P
P′
P
l
P′
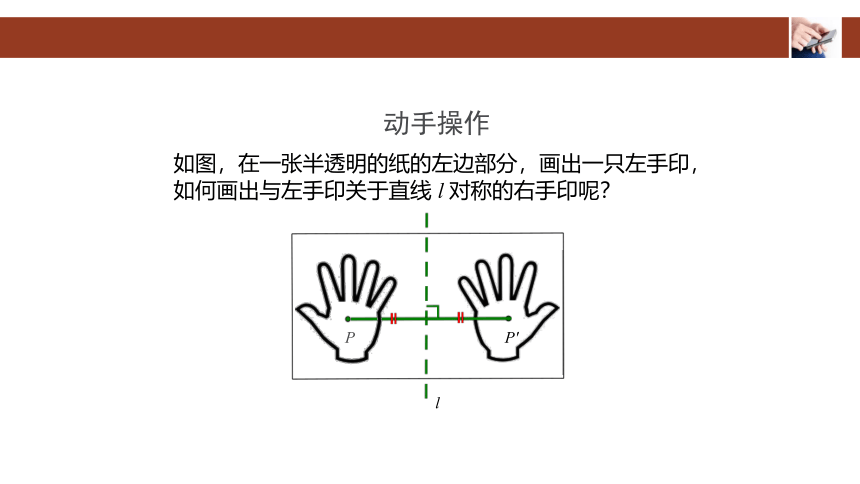
动手操作
如图,在一张半透明的纸的左边部分,画出一只左手印,如何画出与左手印关于直线 l 对称的右手印呢?
由一个平面图形可以得到与它关于一条直线 l 对称的图形,
(3) 连接任意一对对应点的线段被对称
轴垂直平分.
(1)这个图形与原图形的形状、大小完
全相同;
(2)这个图形上的每一点都是原图形上
某一点关于直线 l 的对称点;
P
P′
思考:如果有一个图形和一条直线,如何作出这个图形关于这条直线对称的图形呢?
分析: 点是最基本的几何图形.
点→线→图形.
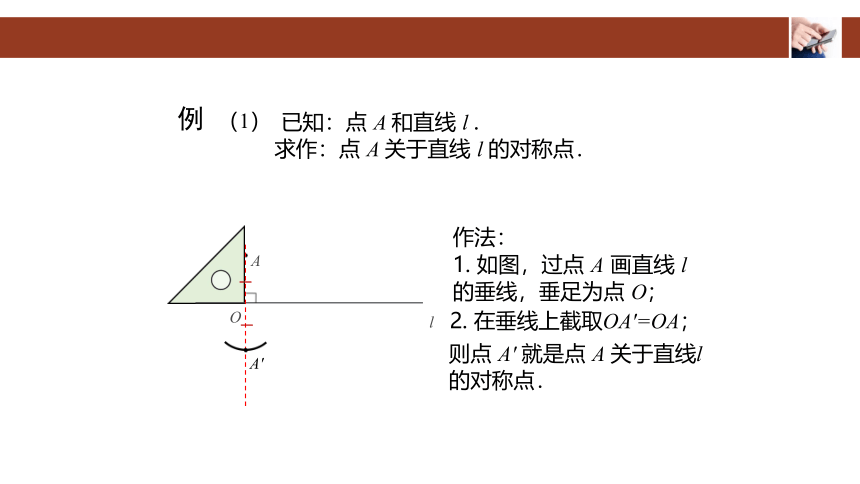
已知:点 A 和直线 l .
求作:点 A 关于直线 l 的对称点.
l
A
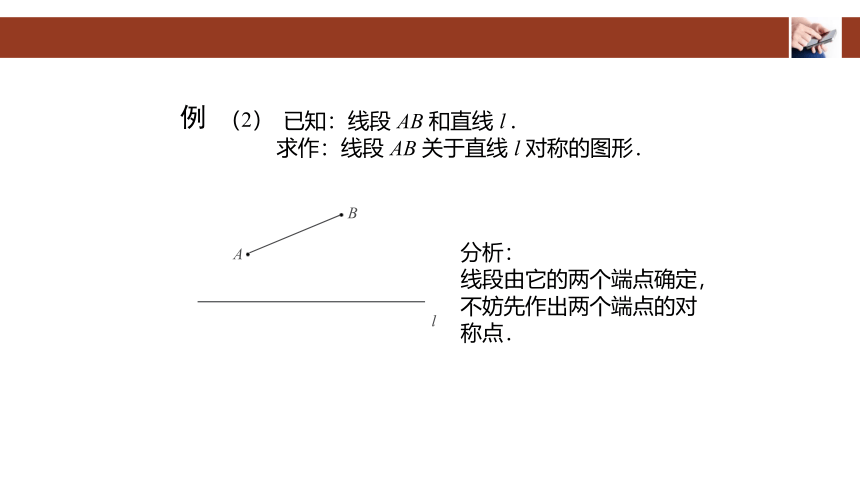
分析:
对应点的连线AA′被对称轴l
垂直平分.
例 (1)
l
A′
O
作法:
则点 A′ 就是点 A 关于直线l 的对称点.
1. 如图,过点 A 画直线 l 的垂线,垂足为点 O;
2. 在垂线上截取OA′=OA;
A
已知:点 A 和直线 l .
求作:点 A 关于直线 l 的对称点.
例 (1)
l
A
分析:
线段由它的两个端点确定,不妨先作出两个端点的对称点.
B
已知:线段 AB 和直线 l .
求作:线段 AB 关于直线 l 对称的图形.
例 (2)
l
A
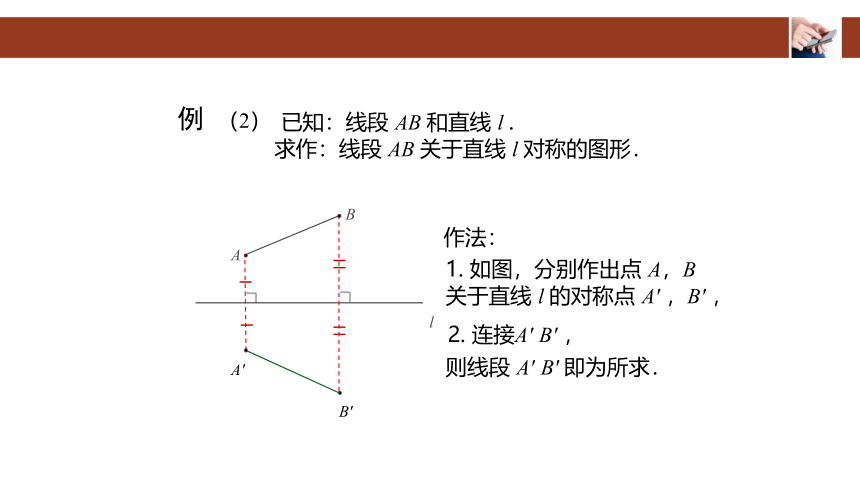
作法:
A′
B
B′
1. 如图,分别作出点 A,B 关于直线 l 的对称点 A′ ,B′ ,
2. 连接A′ B′ ,
则线段 A′ B′ 即为所求.
已知:线段 AB 和直线 l .
求作:线段 AB 关于直线 l 对称的图形.
例 (2)
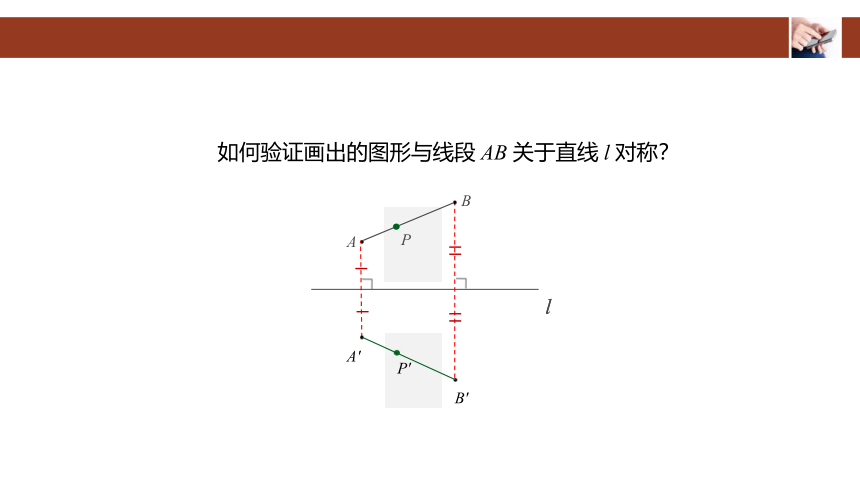
如何验证画出的图形与线段 AB 关于直线 l 对称?
A
A′
B
B′
l
l
P
P′
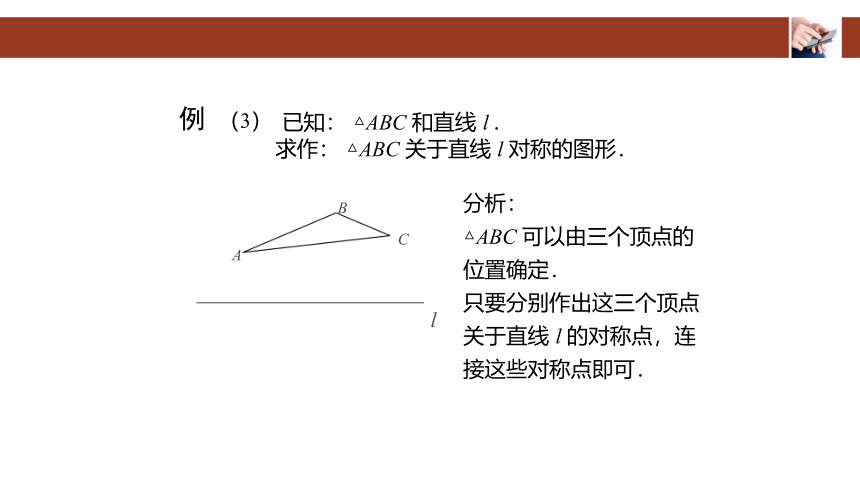
分析:
△ABC 可以由三个顶点的位置确定.
只要分别作出这三个顶点关于直线 l 的对称点,连接这些对称点即可.
l
A
B
C
已知: △ABC 和直线 l .
求作: △ABC 关于直线 l 对称的图形.
例 (3)
l
A
A′
B
C
C′
B′
作法:
1. 如图,分别作出点 A,B , C关于直线 l 的对称点 A′ ,B′ ,C′ ;
2. 连接A′ B′ ,B′ C′ ,C′ A′ ;
则△ A′ B′ C′即为所求.
已知: △ABC和直线 l .
求作: △ABC关于直线 l 对称的图形.
例 (3)
练习 求作△ABC关于直线 l 对称的△A′ B′ C′.
A
B
l
C
练习 求作△ABC关于直线 l 对称的△A′ B′ C′.
甲同学
练习 求作△ABC关于直线 l 对称的△ A′ B′ C′.
乙同学
练习 求作△ABC关于直线 l 对称的△ A′ B′ C′.
丙同学
练习 求作△ABC关于直线 l 对称的△A′ B′ C′.
A
B
l
B′
A′
C′
规范作图!
C
练习 把下列图形补成关于直线 l 对称的图形.
A
B
C
B′
A′
l
(C′)
l
(1)
小结:作已知图形的轴对称图形,
不同的对称轴对应不同的轴对称图形.
(2)
则△ A′ B′ C′即为所求.
练习 把下列图形补成关于直线 l 对称的图形.
(4)
(3)
小结:作已知图形的轴对称图形,
关键在于作出已知图形中一些特殊点的对称点.
l
l
生活中人们常常用轴对称进行进行图案设计.
l
l
几何图形均可看作由点组成,对于某些图形,只要画出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
归纳新知
作已知图形的轴对称图形:
(1)对称轴上的点的对称点就是它本身;
(2)不同的对称轴对应不同的轴对称图形.
例 如图,是一只停泊在平静水面上的小船,它的“倒影”应是图中的( ).
A B C D
l
B
练习 如图,有一个英语单词,三个字母都关于直线 l 对称,请补全字母,补全后的单词是________.
l
BED
BED
例 将一个正方形纸片依次按图1中 a,b的方式对折,然后沿图 c 中的虚线裁剪,成图 d 样式,将纸展开铺平,所得到的图形是图2中的( ).
(图2)
(图1)
A B C D
分析:利用轴对称知识逆回去思考.
D
例 将一个正方形纸片依次按图1中 a,b的方式对折,然后沿图 c 中的虚线裁剪,成图 d 样式,将纸展开铺平,所得到的图形是图2中的( ).
(图2)
(图1)
A B C D
D
动手试一试:如何剪能剪出B 选项?
例 将一个正方形纸片依次按图1中 a,b的方式对折,然后沿图 c 中的虚线裁剪,成图 d 样式,将纸展开铺平,所得到的图形是图2中的( ).
(图2)
(图1)
A B C D
D
B
练习 如图所示,把一个正方形纸片三次对折后沿虚线剪下,则展开铺平纸片所得的图形是( ).
A B C D
C
上折 右折 右下方折 沿虚线剪开
练习 如图所示,把一个正方形纸片三次对折后沿虚线剪下,则展开平纸片所得的图形是( ).
A B C D
C
上折 右折 右下方折 沿虚线剪开
是否能剪出其他几个选项?
若可以,该
怎么剪?
1. 作简单平面图形关于给定对称轴的对称图形.
P
(1)轴对称性质:连接任意一对对应点的线段被对称轴垂直平分.
P′
(2)一般思路:点→线→图形.
关键在于作出图形中一些特殊点的对称点.
(3)不同的对称轴对应不同的轴对称图形.
2. 运用轴对称的性质解决实际问题.
课堂小结
1. 把下面的图形补成关于直线 l 对称的图形.
l
l
l
课后作业
2.将一张长方形纸片按如图①、②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④的纸片展开铺平,则所得到的图案是( ).
A B C D
课后作业
同学们,再见!
复习回顾
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称.这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.
复习回顾
性质 :
1. 如果两个图形关于某直线成轴对称,
那么这两个图形全等.
2. 如果两个图形关于某条直线成轴对称,
那么对称轴是任何一对对应点所连
线段的垂直平分线.
P
P′
P
l
P′
动手操作
如图,在一张半透明的纸的左边部分,画出一只左手印,如何画出与左手印关于直线 l 对称的右手印呢?
由一个平面图形可以得到与它关于一条直线 l 对称的图形,
(3) 连接任意一对对应点的线段被对称
轴垂直平分.
(1)这个图形与原图形的形状、大小完
全相同;
(2)这个图形上的每一点都是原图形上
某一点关于直线 l 的对称点;
P
P′
思考:如果有一个图形和一条直线,如何作出这个图形关于这条直线对称的图形呢?
分析: 点是最基本的几何图形.
点→线→图形.
已知:点 A 和直线 l .
求作:点 A 关于直线 l 的对称点.
l
A
分析:
对应点的连线AA′被对称轴l
垂直平分.
例 (1)
l
A′
O
作法:
则点 A′ 就是点 A 关于直线l 的对称点.
1. 如图,过点 A 画直线 l 的垂线,垂足为点 O;
2. 在垂线上截取OA′=OA;
A
已知:点 A 和直线 l .
求作:点 A 关于直线 l 的对称点.
例 (1)
l
A
分析:
线段由它的两个端点确定,不妨先作出两个端点的对称点.
B
已知:线段 AB 和直线 l .
求作:线段 AB 关于直线 l 对称的图形.
例 (2)
l
A
作法:
A′
B
B′
1. 如图,分别作出点 A,B 关于直线 l 的对称点 A′ ,B′ ,
2. 连接A′ B′ ,
则线段 A′ B′ 即为所求.
已知:线段 AB 和直线 l .
求作:线段 AB 关于直线 l 对称的图形.
例 (2)
如何验证画出的图形与线段 AB 关于直线 l 对称?
A
A′
B
B′
l
l
P
P′
分析:
△ABC 可以由三个顶点的位置确定.
只要分别作出这三个顶点关于直线 l 的对称点,连接这些对称点即可.
l
A
B
C
已知: △ABC 和直线 l .
求作: △ABC 关于直线 l 对称的图形.
例 (3)
l
A
A′
B
C
C′
B′
作法:
1. 如图,分别作出点 A,B , C关于直线 l 的对称点 A′ ,B′ ,C′ ;
2. 连接A′ B′ ,B′ C′ ,C′ A′ ;
则△ A′ B′ C′即为所求.
已知: △ABC和直线 l .
求作: △ABC关于直线 l 对称的图形.
例 (3)
练习 求作△ABC关于直线 l 对称的△A′ B′ C′.
A
B
l
C
练习 求作△ABC关于直线 l 对称的△A′ B′ C′.
甲同学
练习 求作△ABC关于直线 l 对称的△ A′ B′ C′.
乙同学
练习 求作△ABC关于直线 l 对称的△ A′ B′ C′.
丙同学
练习 求作△ABC关于直线 l 对称的△A′ B′ C′.
A
B
l
B′
A′
C′
规范作图!
C
练习 把下列图形补成关于直线 l 对称的图形.
A
B
C
B′
A′
l
(C′)
l
(1)
小结:作已知图形的轴对称图形,
不同的对称轴对应不同的轴对称图形.
(2)
则△ A′ B′ C′即为所求.
练习 把下列图形补成关于直线 l 对称的图形.
(4)
(3)
小结:作已知图形的轴对称图形,
关键在于作出已知图形中一些特殊点的对称点.
l
l
生活中人们常常用轴对称进行进行图案设计.
l
l
几何图形均可看作由点组成,对于某些图形,只要画出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
归纳新知
作已知图形的轴对称图形:
(1)对称轴上的点的对称点就是它本身;
(2)不同的对称轴对应不同的轴对称图形.
例 如图,是一只停泊在平静水面上的小船,它的“倒影”应是图中的( ).
A B C D
l
B
练习 如图,有一个英语单词,三个字母都关于直线 l 对称,请补全字母,补全后的单词是________.
l
BED
BED
例 将一个正方形纸片依次按图1中 a,b的方式对折,然后沿图 c 中的虚线裁剪,成图 d 样式,将纸展开铺平,所得到的图形是图2中的( ).
(图2)
(图1)
A B C D
分析:利用轴对称知识逆回去思考.
D
例 将一个正方形纸片依次按图1中 a,b的方式对折,然后沿图 c 中的虚线裁剪,成图 d 样式,将纸展开铺平,所得到的图形是图2中的( ).
(图2)
(图1)
A B C D
D
动手试一试:如何剪能剪出B 选项?
例 将一个正方形纸片依次按图1中 a,b的方式对折,然后沿图 c 中的虚线裁剪,成图 d 样式,将纸展开铺平,所得到的图形是图2中的( ).
(图2)
(图1)
A B C D
D
B
练习 如图所示,把一个正方形纸片三次对折后沿虚线剪下,则展开铺平纸片所得的图形是( ).
A B C D
C
上折 右折 右下方折 沿虚线剪开
练习 如图所示,把一个正方形纸片三次对折后沿虚线剪下,则展开平纸片所得的图形是( ).
A B C D
C
上折 右折 右下方折 沿虚线剪开
是否能剪出其他几个选项?
若可以,该
怎么剪?
1. 作简单平面图形关于给定对称轴的对称图形.
P
(1)轴对称性质:连接任意一对对应点的线段被对称轴垂直平分.
P′
(2)一般思路:点→线→图形.
关键在于作出图形中一些特殊点的对称点.
(3)不同的对称轴对应不同的轴对称图形.
2. 运用轴对称的性质解决实际问题.
课堂小结
1. 把下面的图形补成关于直线 l 对称的图形.
l
l
l
课后作业
2.将一张长方形纸片按如图①、②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④的纸片展开铺平,则所得到的图案是( ).
A B C D
课后作业
同学们,再见!
