人教版八年级上册13.3.1等腰三角形(第二课时)课件(26张)
文档属性
| 名称 | 人教版八年级上册13.3.1等腰三角形(第二课时)课件(26张) |  | |
| 格式 | pptx | ||
| 文件大小 | 358.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:10:57 | ||
图片预览






文档简介
等腰三角形(第二课时)
知识回顾
性质1:等腰三角形的两个底角相等
(简写成:等边对等角).
A
B
C
应用格式:
∵ AB=AC,
∴ ∠B=∠C(等边对等角).
知识回顾
性质2:等腰三角形顶角的平分线、
底边上的中线及底边上的高线互相重合(简写成:三线合一).
A
B
C
D
应用格式:
∵AB=AC,AD⊥BC,
∴BD=CD, ∠BAD=∠CAD(三线合一).
知识回顾
性质2:等腰三角形顶角的平分线、
底边上的中线及底边上的高线互相重合(简写成:三线合一).
应用格式:
∵AB=AC,BD=CD,
∴ AD⊥BC , ∠BAD=∠CAD(三线合一).
A
B
C
D
知识回顾
性质2:等腰三角形顶角的平分线、
底边上的中线及底边上的高线互相重合(简写成:三线合一).
A
B
C
D
应用格式:
∵AB=AC,∠BAD=∠CAD,
∴ AD⊥BC , DB=DC(三线合一).
如图,位于海上B、C 两处的两艘救生船接到A处遇险船只的报警,当时测得∠B=∠C.如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
A
B
C
情景:动脑思考
已知:如图,在△ABC中, ∠B=∠C,那么它们所对的边AB和AC有什么数量关系?
C
A
B
测量得到:AB=AC
探究:测一测
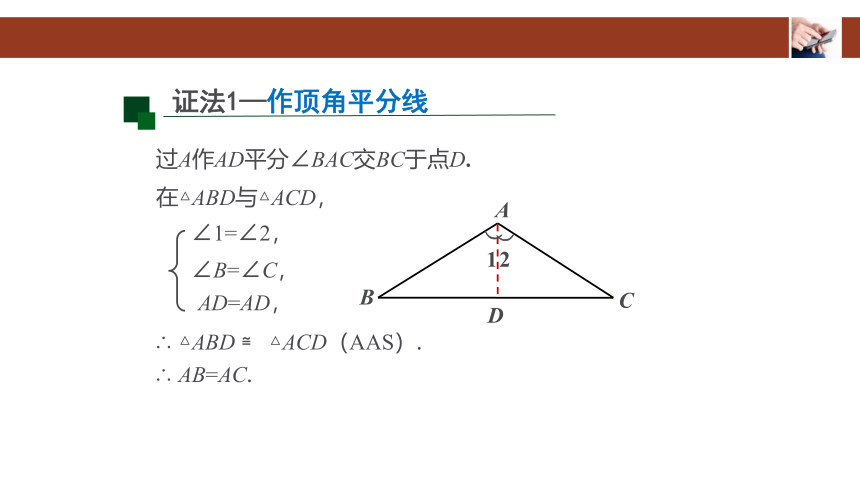
在△ABD与△ACD,
∠1=∠2,
∴ △ABD ≌ △ACD(AAS).
∠B=∠C,
AD=AD,
∴ AB=AC.
过A作AD平分∠BAC交BC于点D.
C
A
B
2
1
D
(
(
证法1—作顶角平分线
在△ABD与△ACD,
∠ADB=∠ADC,
∴ △ABD ≌ △ACD(AAS).
∠B=∠C,
AD=AD,
∴ AB=AC.
过A作AD⊥BC交BC于D,∠ADB=∠ADC=90°.
C
A
B
D
证法2--作底边上的高
在△DBE与△DCF中,
∠DEB=∠DFC,
∴ △DBE ≌ △DFC(AAS).
∠B=∠C,
DB=DC,
∴ DE=DF.
过A作中线AD ,则 DB=DC.
作DE⊥AB,DF⊥AC,垂足分别为E,F.
证法3--作两腰的高
C
A
B
E
F
2
1
D
(
(
证法3--作两腰的高
又DE⊥AB,DF⊥AC,
∴ ∠1=∠2.
∠B=∠C,
∠1=∠2,
BD=CD,
得△ABD≌△ACD(AAS),
∴ AB=AC.
C
A
B
E
F
2
1
D
(
(
∴ AC=AB. (等角对等边)
即△ABC为等腰三角形.
∵∠B=∠C,(已知)
如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角对等边”).
应用格式:
B
C
A
(
(
等腰三角形的判定方法
在△ABC中,
A
B
C
D
2
1
∵∠1=∠2 , ∴ BD=DC.
∵∠1=∠2, ∴ DC=BC.
A
B
C
D
2
1
错,因为都不是在同一个三角形中.
辨析
求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知: ∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.
A
B
C
E
(
(
1
2
D
例题
A
B
C
E
(
(
1
2
D
例题—证明
∵AD∥BC,
∴∠1=∠B( ),
∠2=∠C( ).
又∵∠1=∠2,
∴∠B=∠C.
∴AB=AC( ).
两直线平行,同位角相等
两直线平行,内错角相等
等角对等边
已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形.
a
h
例题—作图
A
B
C
a
h
2.作线段AB的垂直平分线MN,交AB
于点D.
作法:1.作线段AB=a.
3.在MN上取一点C,使DC=h.
4.连接AC,BC,则△ABC即为所求.
A
B
C
M
N
D
例题—作图
课堂练习
已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.
B
A
D
C
课堂练习
已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.
B
A
D
C
证明:∵ AD∥BC,
∴∠ADB=∠DBC.
∵ BD平分∠ABC, ∴∠ABD=∠DBC. ∴∠ABD=∠ADB. ∴AB=AD.
课堂小结:知识内容
等腰三角形的判定:
定义:两条边相等的三角形叫做等腰三角形.
等腰三角形的判定方法:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
课堂小结:数学方法
判定线段之间的数量关系,一般做法是通过全等或利用“等角对等边”,运用转化思想,解决问题.
比较等腰三角形的性质与判定:
“等边对等角”与“等角对等边”,条件与结论是对调的,运用逆向思维观察和思考,可以提升自己的理性思维.
课后作业
1.一个三角形的一个外角为130°,且它恰好等
于一个不相邻的内角的2倍.这个三角形是( ).
A.钝角三角形 B.直角三角形 C.等腰三角形 D.等边三角形
课后作业
2.如图,已知∠A=36°,∠DBC=36°,∠C=72°,则∠DBC=_____,∠BDC=_____,图中的等腰三角形有_______________________.
A
B
C
D
课后作业
3.已知:如图,AB=DC,BD=CA,BD与CA相交于点E.
求证:△AED是等腰三角形.
A
B
C
D
E
课后作业
4. 如图,上午10 时,一条船从A处出发以每小时20海里的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°,∠NBC=80°. 求从B处到灯塔C的距离.
80°
40°
N
B
A
C
北
同学们,再见!
知识回顾
性质1:等腰三角形的两个底角相等
(简写成:等边对等角).
A
B
C
应用格式:
∵ AB=AC,
∴ ∠B=∠C(等边对等角).
知识回顾
性质2:等腰三角形顶角的平分线、
底边上的中线及底边上的高线互相重合(简写成:三线合一).
A
B
C
D
应用格式:
∵AB=AC,AD⊥BC,
∴BD=CD, ∠BAD=∠CAD(三线合一).
知识回顾
性质2:等腰三角形顶角的平分线、
底边上的中线及底边上的高线互相重合(简写成:三线合一).
应用格式:
∵AB=AC,BD=CD,
∴ AD⊥BC , ∠BAD=∠CAD(三线合一).
A
B
C
D
知识回顾
性质2:等腰三角形顶角的平分线、
底边上的中线及底边上的高线互相重合(简写成:三线合一).
A
B
C
D
应用格式:
∵AB=AC,∠BAD=∠CAD,
∴ AD⊥BC , DB=DC(三线合一).
如图,位于海上B、C 两处的两艘救生船接到A处遇险船只的报警,当时测得∠B=∠C.如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
A
B
C
情景:动脑思考
已知:如图,在△ABC中, ∠B=∠C,那么它们所对的边AB和AC有什么数量关系?
C
A
B
测量得到:AB=AC
探究:测一测
在△ABD与△ACD,
∠1=∠2,
∴ △ABD ≌ △ACD(AAS).
∠B=∠C,
AD=AD,
∴ AB=AC.
过A作AD平分∠BAC交BC于点D.
C
A
B
2
1
D
(
(
证法1—作顶角平分线
在△ABD与△ACD,
∠ADB=∠ADC,
∴ △ABD ≌ △ACD(AAS).
∠B=∠C,
AD=AD,
∴ AB=AC.
过A作AD⊥BC交BC于D,∠ADB=∠ADC=90°.
C
A
B
D
证法2--作底边上的高
在△DBE与△DCF中,
∠DEB=∠DFC,
∴ △DBE ≌ △DFC(AAS).
∠B=∠C,
DB=DC,
∴ DE=DF.
过A作中线AD ,则 DB=DC.
作DE⊥AB,DF⊥AC,垂足分别为E,F.
证法3--作两腰的高
C
A
B
E
F
2
1
D
(
(
证法3--作两腰的高
又DE⊥AB,DF⊥AC,
∴ ∠1=∠2.
∠B=∠C,
∠1=∠2,
BD=CD,
得△ABD≌△ACD(AAS),
∴ AB=AC.
C
A
B
E
F
2
1
D
(
(
∴ AC=AB. (等角对等边)
即△ABC为等腰三角形.
∵∠B=∠C,(已知)
如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角对等边”).
应用格式:
B
C
A
(
(
等腰三角形的判定方法
在△ABC中,
A
B
C
D
2
1
∵∠1=∠2 , ∴ BD=DC.
∵∠1=∠2, ∴ DC=BC.
A
B
C
D
2
1
错,因为都不是在同一个三角形中.
辨析
求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知: ∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.
A
B
C
E
(
(
1
2
D
例题
A
B
C
E
(
(
1
2
D
例题—证明
∵AD∥BC,
∴∠1=∠B( ),
∠2=∠C( ).
又∵∠1=∠2,
∴∠B=∠C.
∴AB=AC( ).
两直线平行,同位角相等
两直线平行,内错角相等
等角对等边
已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形.
a
h
例题—作图
A
B
C
a
h
2.作线段AB的垂直平分线MN,交AB
于点D.
作法:1.作线段AB=a.
3.在MN上取一点C,使DC=h.
4.连接AC,BC,则△ABC即为所求.
A
B
C
M
N
D
例题—作图
课堂练习
已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.
B
A
D
C
课堂练习
已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.
B
A
D
C
证明:∵ AD∥BC,
∴∠ADB=∠DBC.
∵ BD平分∠ABC, ∴∠ABD=∠DBC. ∴∠ABD=∠ADB. ∴AB=AD.
课堂小结:知识内容
等腰三角形的判定:
定义:两条边相等的三角形叫做等腰三角形.
等腰三角形的判定方法:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
课堂小结:数学方法
判定线段之间的数量关系,一般做法是通过全等或利用“等角对等边”,运用转化思想,解决问题.
比较等腰三角形的性质与判定:
“等边对等角”与“等角对等边”,条件与结论是对调的,运用逆向思维观察和思考,可以提升自己的理性思维.
课后作业
1.一个三角形的一个外角为130°,且它恰好等
于一个不相邻的内角的2倍.这个三角形是( ).
A.钝角三角形 B.直角三角形 C.等腰三角形 D.等边三角形
课后作业
2.如图,已知∠A=36°,∠DBC=36°,∠C=72°,则∠DBC=_____,∠BDC=_____,图中的等腰三角形有_______________________.
A
B
C
D
课后作业
3.已知:如图,AB=DC,BD=CA,BD与CA相交于点E.
求证:△AED是等腰三角形.
A
B
C
D
E
课后作业
4. 如图,上午10 时,一条船从A处出发以每小时20海里的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°,∠NBC=80°. 求从B处到灯塔C的距离.
80°
40°
N
B
A
C
北
同学们,再见!
