人教版八年级上册13.3等腰三角形的综合运用(第二课时)课件(20张)
文档属性
| 名称 | 人教版八年级上册13.3等腰三角形的综合运用(第二课时)课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 222.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:12:40 | ||
图片预览




文档简介
等腰三角形的综合运用(第二课时)
利用等腰三角形的判定和性质:
(1)判断三角形形状;
(2)计算三角形边长及角度;
(3)证明几何图形中线段相等.
知识运用
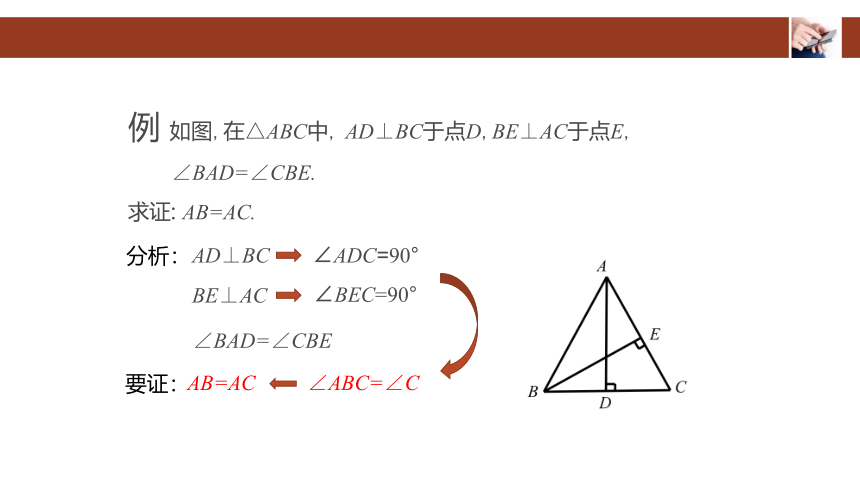
例 如图,在△ABC中, AD⊥BC于点D,BE⊥AC于点E,
∠BAD=∠CBE.
求证: AB=AC.
分析:
AD⊥BC
∠ADC=90°
BE⊥AC
∠BEC=90°
∠BAD=∠CBE
AB=AC
∠ABC=∠C
要证:
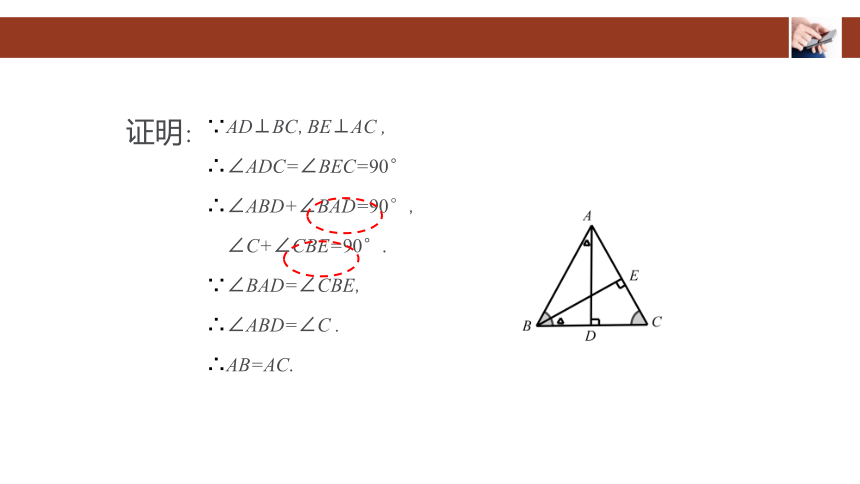
∵AD⊥BC,BE⊥AC ,
∴∠ADC=∠BEC=90°
∴∠ABD+∠BAD=90°,
∠C+∠CBE=90°.
∵∠BAD=∠CBE,
∴∠ABD=∠C .
∴AB=AC.
证明:
证明两条线段相等,当这两条线段是同一个三角形的边时,一般我们先证明这两条线段所对的角相等,然后根据等腰三角形的判定方法“等角对等边”,即可证明这两条线段相等.
当题目条件中直角比较多时,一般用“同角或等角的余角相等”来证明两角相等.
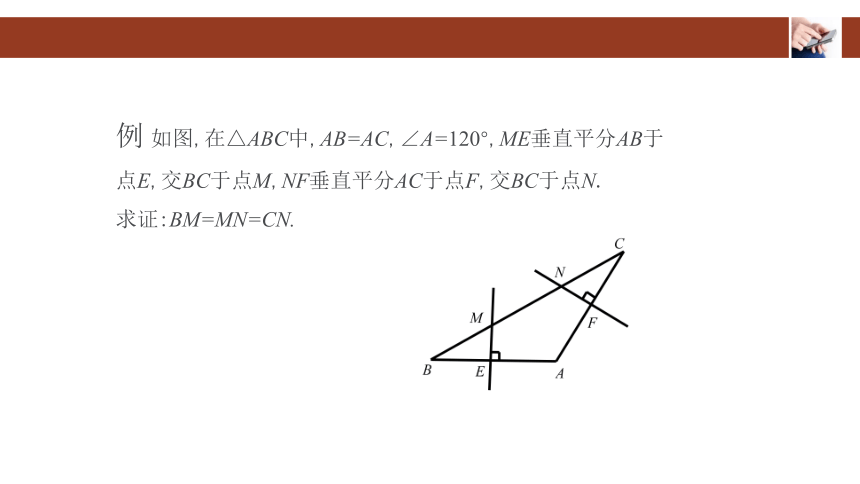
例 如图,在△ABC中,AB=AC,∠A=120°,ME垂直平分AB于点E,交BC于点M,NF垂直平分AC于点F,交BC于点N.
求证:BM=MN=CN.
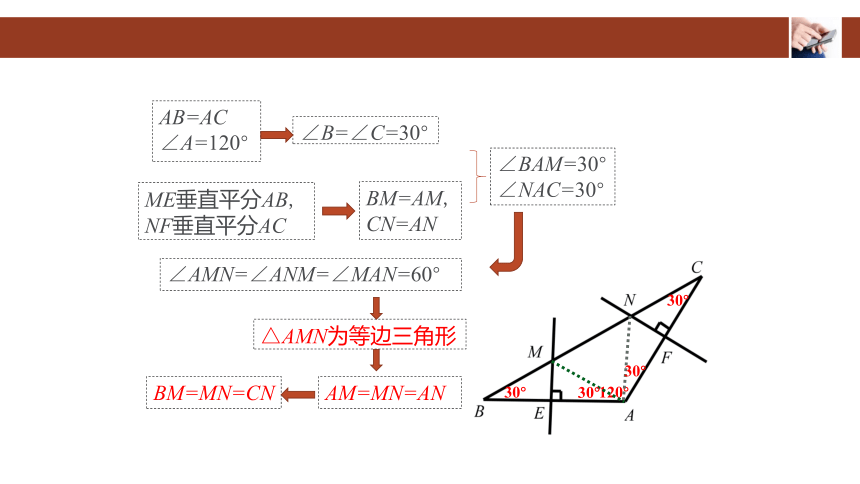
AB=AC
∠A=120°
?
?
?
∠B=∠C=30°
BM=AM,
CN=AN
ME垂直平分AB,
NF垂直平分AC
?
?
∠BAM=30°
∠NAC=30°
∠AMN=∠ANM=∠MAN=60°
BM=MN=CN
AM=MN=AN
△AMN为等边三角形
120°
30°
30°
30°
30°
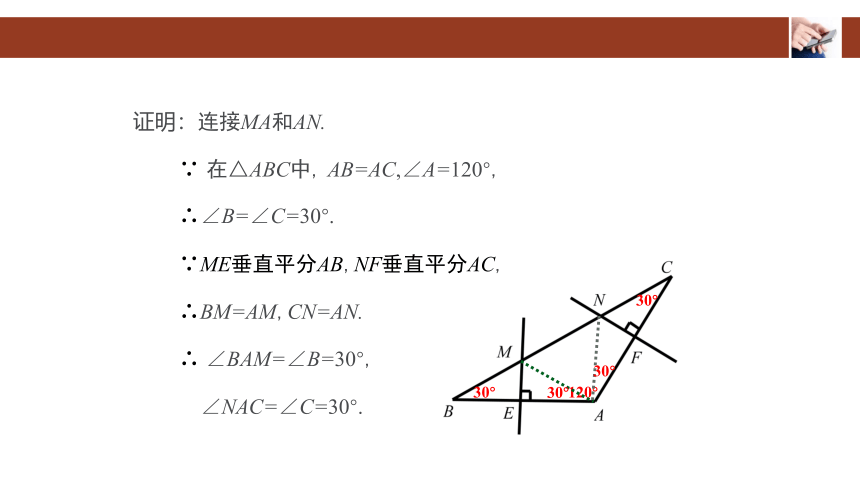
证明:连接MA和AN.
∵ 在△ABC中, AB=AC,∠A=120°,
∴∠B=∠C=30°.
∵ME垂直平分AB,NF垂直平分AC,
∴BM=AM,CN=AN.
∴ ∠BAM=∠B=30°,
∠NAC=∠C=30°.
、
120°
30°
30°
30°
30°
证明: ∴∠AMN=∠B+∠BAM=60°,
∠ANM=∠C+∠NAC=60°.
∴∠MAN=180°-∠AMN -∠ANM=60°.
∴△AMN为等边三角形.
∴AM=MN=AN.
∵BM=AM,CN=AN,
∴BM=MN=CN.
、
120°
30°
30°
30°
30°
一般地,当题目中出现垂直平分线时,我们会经常使用垂直平分线的性质“线段垂直平分线上的点到线段两个端点距离相等”,来证明线段的相等,或结合等腰(边)三角形边角关系进行线段转化,来证明目标线段相等.
例 如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,
求证:BD=CE
、
分析:
AB=AC
AD=AE
BD=CE
要证:
△ABD ≌△ACE
∠BAD=∠CAE
∠B=∠C
∠ADE=∠AED
证明:
∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED.
∴∠ADE -∠B=∠AED -∠C.
即∠BAD=∠CAE.
证明:
在△ABD和△ACE中,
AB=AC ,
∠BAD=∠CAE,
AD=AE.
∴△ABD ≌ △ACE (SAS).
∴BD=CE.
利用全等三角形是证明线段相等的一个很好方法,往往我们在等腰三角形中,会利用特有的边角关系来构造全等三角形.
等腰三角形
边角关系
构造全等三角形
线段相等
其他解法:如果过点A做AO⊥BC于点O
O
AB=AC
BO=CO
AD=AE
DO=EO
BO -DO=CO -EO
BD=CE
?
?
AO 三线合一
课堂小结
证明线段相等的常见方法:
(1)利用等腰三角形的性质和判定证明线段相等;
(2)利用垂直平分线的性质和判定证明线段相等;
(3)利用全等三角形的性质证明线段相等.
课后作业
1. 已知:如图,AC和BD相交于点O,AB//CD,OA=OB,
求证:OC=OD.
2.如图,在等边三角形△ABC中,∠ABC和∠ACB的平分线相交于点O,OB和OC的垂直平分线EE'和FF'分别交BC于点E和F,连接OE,OF.
证明:AB=3EF.
3. 如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB,∠EDF=60°,其两边分别交边AB,AC于点E和F.
(1) 求证:△ABD是等边三角形;
(2) 求证:BE=AF.
同学们,再见!
利用等腰三角形的判定和性质:
(1)判断三角形形状;
(2)计算三角形边长及角度;
(3)证明几何图形中线段相等.
知识运用
例 如图,在△ABC中, AD⊥BC于点D,BE⊥AC于点E,
∠BAD=∠CBE.
求证: AB=AC.
分析:
AD⊥BC
∠ADC=90°
BE⊥AC
∠BEC=90°
∠BAD=∠CBE
AB=AC
∠ABC=∠C
要证:
∵AD⊥BC,BE⊥AC ,
∴∠ADC=∠BEC=90°
∴∠ABD+∠BAD=90°,
∠C+∠CBE=90°.
∵∠BAD=∠CBE,
∴∠ABD=∠C .
∴AB=AC.
证明:
证明两条线段相等,当这两条线段是同一个三角形的边时,一般我们先证明这两条线段所对的角相等,然后根据等腰三角形的判定方法“等角对等边”,即可证明这两条线段相等.
当题目条件中直角比较多时,一般用“同角或等角的余角相等”来证明两角相等.
例 如图,在△ABC中,AB=AC,∠A=120°,ME垂直平分AB于点E,交BC于点M,NF垂直平分AC于点F,交BC于点N.
求证:BM=MN=CN.
AB=AC
∠A=120°
?
?
?
∠B=∠C=30°
BM=AM,
CN=AN
ME垂直平分AB,
NF垂直平分AC
?
?
∠BAM=30°
∠NAC=30°
∠AMN=∠ANM=∠MAN=60°
BM=MN=CN
AM=MN=AN
△AMN为等边三角形
120°
30°
30°
30°
30°
证明:连接MA和AN.
∵ 在△ABC中, AB=AC,∠A=120°,
∴∠B=∠C=30°.
∵ME垂直平分AB,NF垂直平分AC,
∴BM=AM,CN=AN.
∴ ∠BAM=∠B=30°,
∠NAC=∠C=30°.
、
120°
30°
30°
30°
30°
证明: ∴∠AMN=∠B+∠BAM=60°,
∠ANM=∠C+∠NAC=60°.
∴∠MAN=180°-∠AMN -∠ANM=60°.
∴△AMN为等边三角形.
∴AM=MN=AN.
∵BM=AM,CN=AN,
∴BM=MN=CN.
、
120°
30°
30°
30°
30°
一般地,当题目中出现垂直平分线时,我们会经常使用垂直平分线的性质“线段垂直平分线上的点到线段两个端点距离相等”,来证明线段的相等,或结合等腰(边)三角形边角关系进行线段转化,来证明目标线段相等.
例 如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,
求证:BD=CE
、
分析:
AB=AC
AD=AE
BD=CE
要证:
△ABD ≌△ACE
∠BAD=∠CAE
∠B=∠C
∠ADE=∠AED
证明:
∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED.
∴∠ADE -∠B=∠AED -∠C.
即∠BAD=∠CAE.
证明:
在△ABD和△ACE中,
AB=AC ,
∠BAD=∠CAE,
AD=AE.
∴△ABD ≌ △ACE (SAS).
∴BD=CE.
利用全等三角形是证明线段相等的一个很好方法,往往我们在等腰三角形中,会利用特有的边角关系来构造全等三角形.
等腰三角形
边角关系
构造全等三角形
线段相等
其他解法:如果过点A做AO⊥BC于点O
O
AB=AC
BO=CO
AD=AE
DO=EO
BO -DO=CO -EO
BD=CE
?
?
AO 三线合一
课堂小结
证明线段相等的常见方法:
(1)利用等腰三角形的性质和判定证明线段相等;
(2)利用垂直平分线的性质和判定证明线段相等;
(3)利用全等三角形的性质证明线段相等.
课后作业
1. 已知:如图,AC和BD相交于点O,AB//CD,OA=OB,
求证:OC=OD.
2.如图,在等边三角形△ABC中,∠ABC和∠ACB的平分线相交于点O,OB和OC的垂直平分线EE'和FF'分别交BC于点E和F,连接OE,OF.
证明:AB=3EF.
3. 如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB,∠EDF=60°,其两边分别交边AB,AC于点E和F.
(1) 求证:△ABD是等边三角形;
(2) 求证:BE=AF.
同学们,再见!
