人教版八年级上册13.3等腰三角形的综合运用(第一课时)课件(22张)
文档属性
| 名称 | 人教版八年级上册13.3等腰三角形的综合运用(第一课时)课件(22张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 231.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览





文档简介
等腰三角形的综合运用(第一课时)
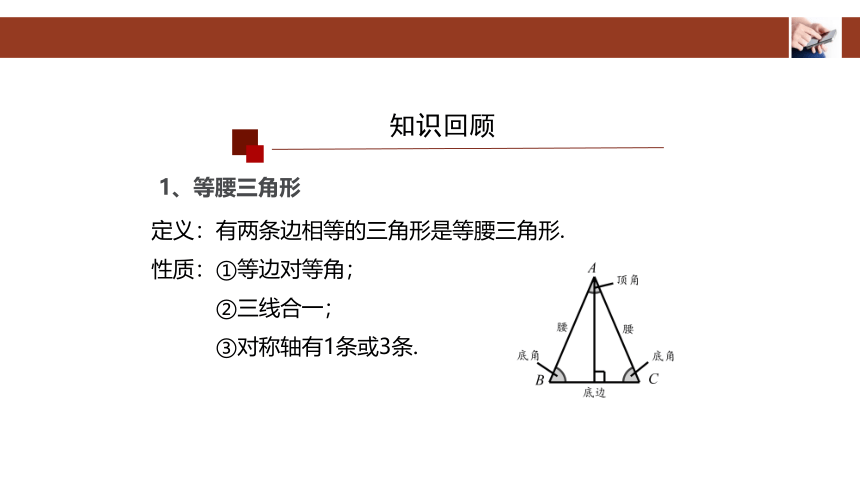
1、等腰三角形
定义:有两条边相等的三角形是等腰三角形.
性质:①等边对等角;
②三线合一;
③对称轴有1条或3条.
知识回顾
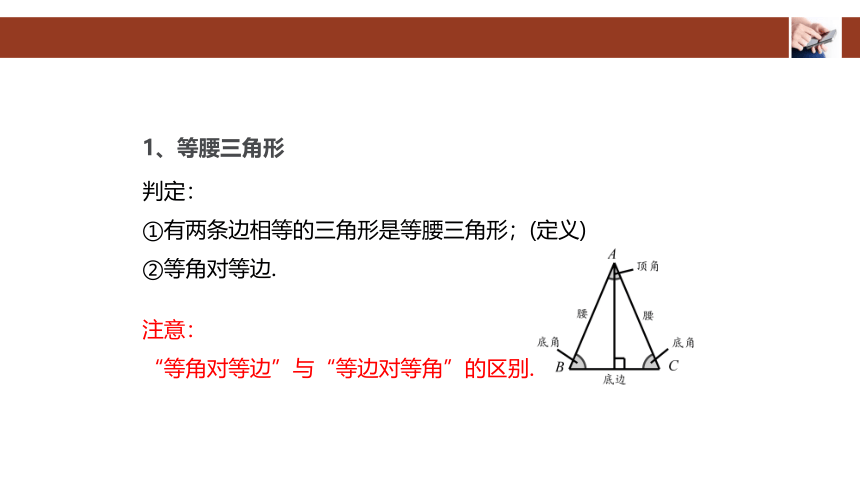
1、等腰三角形
判定:
①有两条边相等的三角形是等腰三角形;(定义)
②等角对等边.
注意:
“等角对等边”与“等边对等角”的区别.
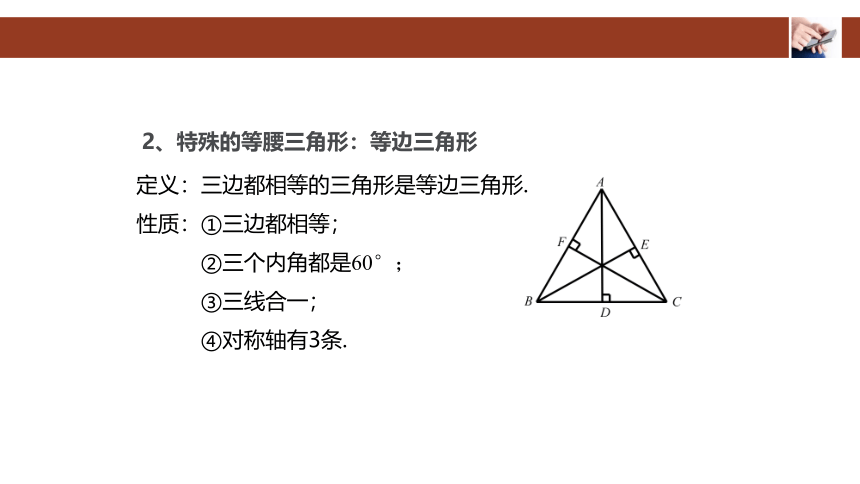
2、特殊的等腰三角形:等边三角形
定义:三边都相等的三角形是等边三角形.
性质:①三边都相等;
②三个内角都是60°;
③三线合一;
④对称轴有3条.
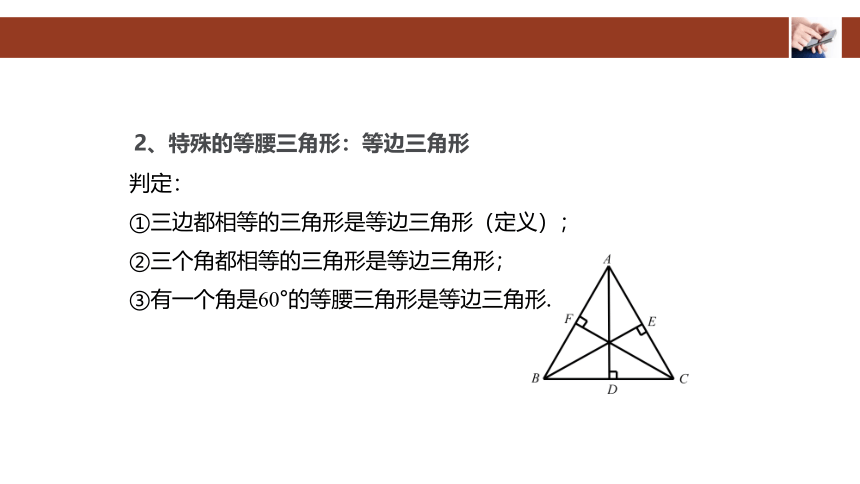
判定:
①三边都相等的三角形是等边三角形(定义);
②三个角都相等的三角形是等边三角形;
③有一个角是60°的等腰三角形是等边三角形.
2、特殊的等腰三角形:等边三角形
一、运用等腰三角形的判定知识进行三角形形状的判断
例 已知三角形△ABC的三边长为a,b,c.
(1)∠A=70°, ∠B=40°,则三角形的形状为________;
(2)∠A:∠B:∠C=1:1:2, 则三角形的形状为________;
(3)当满足(a-b)(b-c)(c-a)=0时,则三角形的形状为_______;
(4)当满足(a-b)?+(b-c)?+(c-a)?=0时,则三角形的形状为_____.
知识运用
例 已知三角形△ABC的三边长为a,b,c.
(1)∠A=70°, ∠B=40°,则三角形的形状为____________.
分析:∵∠A=70°, ∠B=40°,
∴∠C=180°-∠A-∠B=70°.
∴∠A=∠C.
根据“等角对等边”.
∴△ABC是等腰三角形.
等腰三角形
例 已知三角形△ABC的三边长为a,b,c.
(2)∠A:∠B:∠C=1:1:2, 则三角形的形状为______________.
∴∠A=∠B=45°,∠C =45°×2 = 90°.
根据“等角对等边”和直角三角形定义,得
∴△ABC是等腰直角三角形.
等腰直角三角形
∵
分析:
例 已知三角形△ABC的三边长为a,b,c,
(3)当满足(a-b)(b-c)(c-a)=0时,则三角形的形状为__________;
分析:∵(a-b)(b-c)(c-a)=0,
∴a-b,b-c,c-a 中至少有一个为0.
即a-b=0,或b-c=0,或c-a=0.
∴ a=b 或 b=c 或 c=a.
根据等腰三角形定义,得
∴△ABC是等腰三角形.
等腰三角形
例 已知三角形△ABC的三边长为a,b,c.
(4)当满足(a-b)?+(b-c)?+(c-a)?=0时,则三角形的形状为
.
分析: ∵(a-b)?+(b-c)?+(c-a)?=0;
(a-b)?,(b-c)?,(c-a)? 均具有非负性,
∴(a-b)?=0,且(b-c)?=0,且(c-a)?=0.
∴a=b 且 b=c 且 c=a.
根据等边三角形定义,得△ABC是等边三角形.
等边三角形
一般地,判断三角形形状的关键在于要先求出三角形的三个内角度数或三条边长,或找到角(边)所满足的重要数量关系,然后再利用等腰(等边)三角形的判定方法,进行三角形形状的判断.
二、运用等腰三角形的判定和性质进行边角等有关计算
知识运用
例 如图,在△ABC中,AB=AC,∠A=40°,DE垂直平分AB交AC于点D,求∠DBC=______.
?
AB=AC
∠A=40°
DE垂直平分AB
△ABC是等腰三角形
∠ABC=∠C=70°
AD=BD
△ABD是等腰三角形
∠ABD=∠A=40°
∠ADB=100°
分析:
30°
变式: 如图,在△ABC中,∠ABC=120°,点D,E分别在AC和AB上,且AE=ED=DB=BC,若∠A的度数为x°,则用x的代数式表示∠C为____,并求∠A=____°.
∠ABC=120°
分析:
AE=ED=DB=BC
等腰三角形:△AED,△EDB,△BCD.
变式: 如图,在△ABC中,∠ABC=120°,点D,E分别在AC和AB上,且AE=ED=DB=BC,若∠A的度数为x°,则用x的代数式表示∠C为_____,并求∠A=____°.
分析:在△ABC中,
∵∠A+∠ABC+∠C=180°,
∴x°+120°+3x°=180°.
∴x=15.
∴∠A=15°.
3x°
15
x°
2x°
2x°
3x°
3x°
一般地,求等腰三角形中角的度数问题,我们主要依据“等边对等角”性质,三角形内角和定理和外角性质,由已知角逐步推导计算出未知角的度数.或者必要时,通过合理设元,利用方程的思想求解出未知角的度数.
例 如图,△ABC是等边三角形,AD⊥BC,DE⊥AB,垂足分别为D,E.若AB=8,则BD=_____,BE=_____.?
4
2
等边三角形△ABC
分析:
AB=AC=BC=8
∠BAC=∠B=∠C=60°
AD⊥BC
DE⊥AB
AB=8
AD: 三线合一
∠BED=∠AED=90°
∠BDE=30°
?
?
本课小结
(1)复习等腰三角形和等边三角形定义、性质和判定;
(2)学习运用等腰三角形的判定知识进行三角形形状的判断;
(3)学习综合运用等腰三角形的判定和性质进行三角形边角等有关问题的计算.
课后作业
1.如图,在△ABC中,AB=AC,∠BAC=120°,DE垂直平分
AC,交BC于点D,垂足为点E.若DE=2 cm,DC=____ cm,
BC=____ cm.
2.若D为△ABC的边BC上一点,且AD=BD,AB=AC=CD,
则∠B=_______°.
3.如图,在△ABC中,∠BAC=90°,∠C=30°,AD是BC边上的高,BE是角平分线,AD与BE相交于点F,求证:△AEF是等边三角形.
同学们,再见!
1、等腰三角形
定义:有两条边相等的三角形是等腰三角形.
性质:①等边对等角;
②三线合一;
③对称轴有1条或3条.
知识回顾
1、等腰三角形
判定:
①有两条边相等的三角形是等腰三角形;(定义)
②等角对等边.
注意:
“等角对等边”与“等边对等角”的区别.
2、特殊的等腰三角形:等边三角形
定义:三边都相等的三角形是等边三角形.
性质:①三边都相等;
②三个内角都是60°;
③三线合一;
④对称轴有3条.
判定:
①三边都相等的三角形是等边三角形(定义);
②三个角都相等的三角形是等边三角形;
③有一个角是60°的等腰三角形是等边三角形.
2、特殊的等腰三角形:等边三角形
一、运用等腰三角形的判定知识进行三角形形状的判断
例 已知三角形△ABC的三边长为a,b,c.
(1)∠A=70°, ∠B=40°,则三角形的形状为________;
(2)∠A:∠B:∠C=1:1:2, 则三角形的形状为________;
(3)当满足(a-b)(b-c)(c-a)=0时,则三角形的形状为_______;
(4)当满足(a-b)?+(b-c)?+(c-a)?=0时,则三角形的形状为_____.
知识运用
例 已知三角形△ABC的三边长为a,b,c.
(1)∠A=70°, ∠B=40°,则三角形的形状为____________.
分析:∵∠A=70°, ∠B=40°,
∴∠C=180°-∠A-∠B=70°.
∴∠A=∠C.
根据“等角对等边”.
∴△ABC是等腰三角形.
等腰三角形
例 已知三角形△ABC的三边长为a,b,c.
(2)∠A:∠B:∠C=1:1:2, 则三角形的形状为______________.
∴∠A=∠B=45°,∠C =45°×2 = 90°.
根据“等角对等边”和直角三角形定义,得
∴△ABC是等腰直角三角形.
等腰直角三角形
∵
分析:
例 已知三角形△ABC的三边长为a,b,c,
(3)当满足(a-b)(b-c)(c-a)=0时,则三角形的形状为__________;
分析:∵(a-b)(b-c)(c-a)=0,
∴a-b,b-c,c-a 中至少有一个为0.
即a-b=0,或b-c=0,或c-a=0.
∴ a=b 或 b=c 或 c=a.
根据等腰三角形定义,得
∴△ABC是等腰三角形.
等腰三角形
例 已知三角形△ABC的三边长为a,b,c.
(4)当满足(a-b)?+(b-c)?+(c-a)?=0时,则三角形的形状为
.
分析: ∵(a-b)?+(b-c)?+(c-a)?=0;
(a-b)?,(b-c)?,(c-a)? 均具有非负性,
∴(a-b)?=0,且(b-c)?=0,且(c-a)?=0.
∴a=b 且 b=c 且 c=a.
根据等边三角形定义,得△ABC是等边三角形.
等边三角形
一般地,判断三角形形状的关键在于要先求出三角形的三个内角度数或三条边长,或找到角(边)所满足的重要数量关系,然后再利用等腰(等边)三角形的判定方法,进行三角形形状的判断.
二、运用等腰三角形的判定和性质进行边角等有关计算
知识运用
例 如图,在△ABC中,AB=AC,∠A=40°,DE垂直平分AB交AC于点D,求∠DBC=______.
?
AB=AC
∠A=40°
DE垂直平分AB
△ABC是等腰三角形
∠ABC=∠C=70°
AD=BD
△ABD是等腰三角形
∠ABD=∠A=40°
∠ADB=100°
分析:
30°
变式: 如图,在△ABC中,∠ABC=120°,点D,E分别在AC和AB上,且AE=ED=DB=BC,若∠A的度数为x°,则用x的代数式表示∠C为____,并求∠A=____°.
∠ABC=120°
分析:
AE=ED=DB=BC
等腰三角形:△AED,△EDB,△BCD.
变式: 如图,在△ABC中,∠ABC=120°,点D,E分别在AC和AB上,且AE=ED=DB=BC,若∠A的度数为x°,则用x的代数式表示∠C为_____,并求∠A=____°.
分析:在△ABC中,
∵∠A+∠ABC+∠C=180°,
∴x°+120°+3x°=180°.
∴x=15.
∴∠A=15°.
3x°
15
x°
2x°
2x°
3x°
3x°
一般地,求等腰三角形中角的度数问题,我们主要依据“等边对等角”性质,三角形内角和定理和外角性质,由已知角逐步推导计算出未知角的度数.或者必要时,通过合理设元,利用方程的思想求解出未知角的度数.
例 如图,△ABC是等边三角形,AD⊥BC,DE⊥AB,垂足分别为D,E.若AB=8,则BD=_____,BE=_____.?
4
2
等边三角形△ABC
分析:
AB=AC=BC=8
∠BAC=∠B=∠C=60°
AD⊥BC
DE⊥AB
AB=8
AD: 三线合一
∠BED=∠AED=90°
∠BDE=30°
?
?
本课小结
(1)复习等腰三角形和等边三角形定义、性质和判定;
(2)学习运用等腰三角形的判定知识进行三角形形状的判断;
(3)学习综合运用等腰三角形的判定和性质进行三角形边角等有关问题的计算.
课后作业
1.如图,在△ABC中,AB=AC,∠BAC=120°,DE垂直平分
AC,交BC于点D,垂足为点E.若DE=2 cm,DC=____ cm,
BC=____ cm.
2.若D为△ABC的边BC上一点,且AD=BD,AB=AC=CD,
则∠B=_______°.
3.如图,在△ABC中,∠BAC=90°,∠C=30°,AD是BC边上的高,BE是角平分线,AD与BE相交于点F,求证:△AEF是等边三角形.
同学们,再见!
