人教版八年级上册第十一章三角形:与三角形有关的角的综合运用课件(36张)
文档属性
| 名称 | 人教版八年级上册第十一章三角形:与三角形有关的角的综合运用课件(36张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 442.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 00:00:00 | ||
图片预览




文档简介
与三角形有关的角的综合运用
复习回顾
与三角形的角有关的结论有哪些?
三角形的内角和等于180°;
三角形的一个外角等于与它不相邻的两个内角的和.
直角三角形的两个锐角互余;
∴∠2= 180°- 40°= 140°.
∴∠1=40°.
三角形内角和定理
∵∠2= 60°+ 80°= 140°,
∴∠1= 180° - ∠2 = 40°.
三角形外角性质
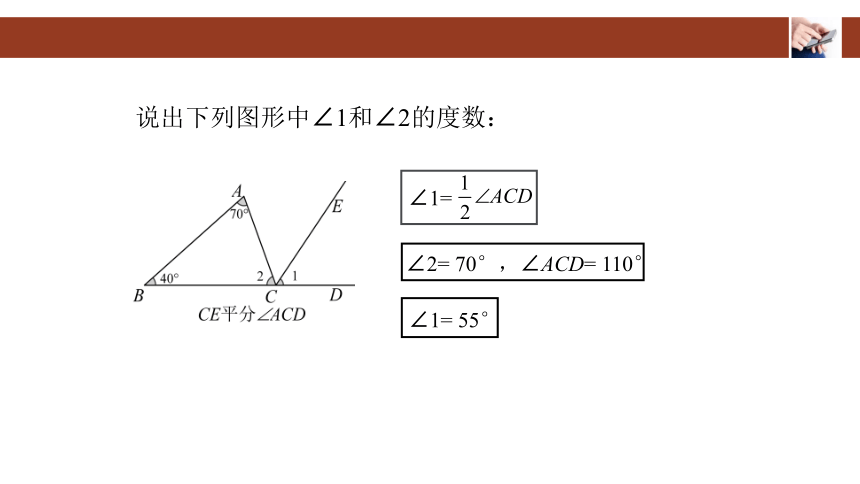
说出下列图形中∠1和∠2的度数:
说出下列图形中∠1和∠2的度数:
∠1=
∠2= 70°,∠ACD= 110°
∠1= 55°
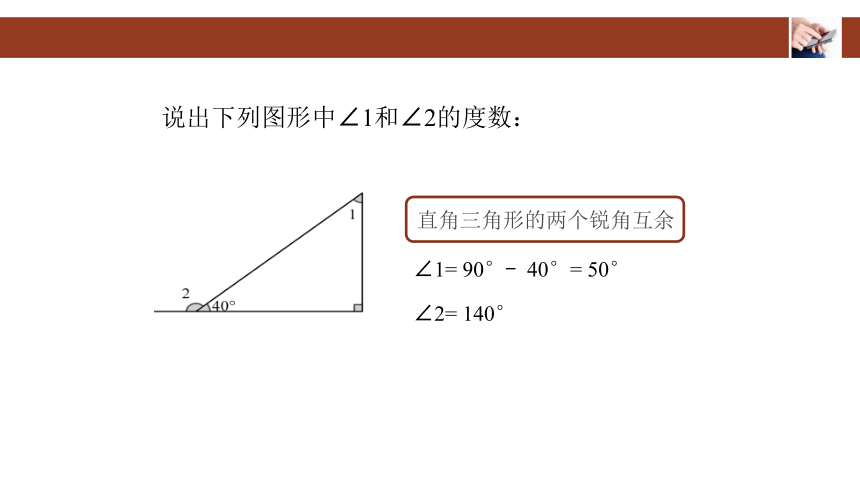
说出下列图形中∠1和∠2的度数:
∠2= 140°
∠1= 90°- 40°= 50°
直角三角形的两个锐角互余
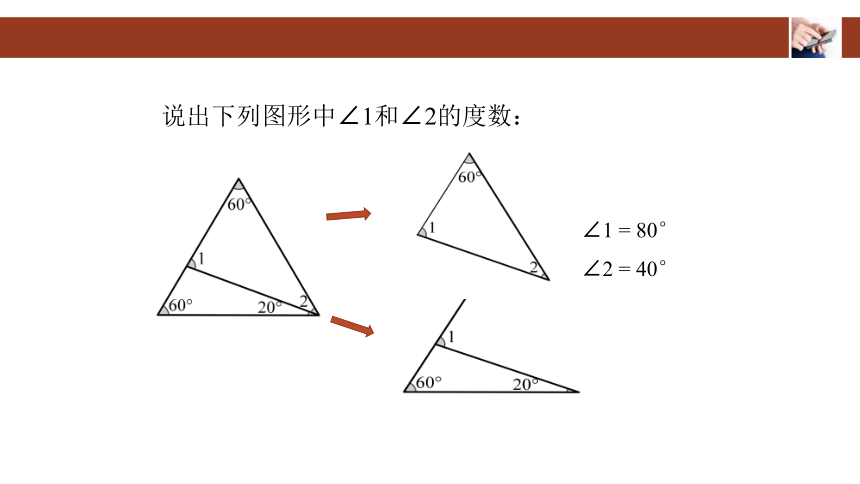
说出下列图形中∠1和∠2的度数:
∠1 = 80°
∠2 = 40°
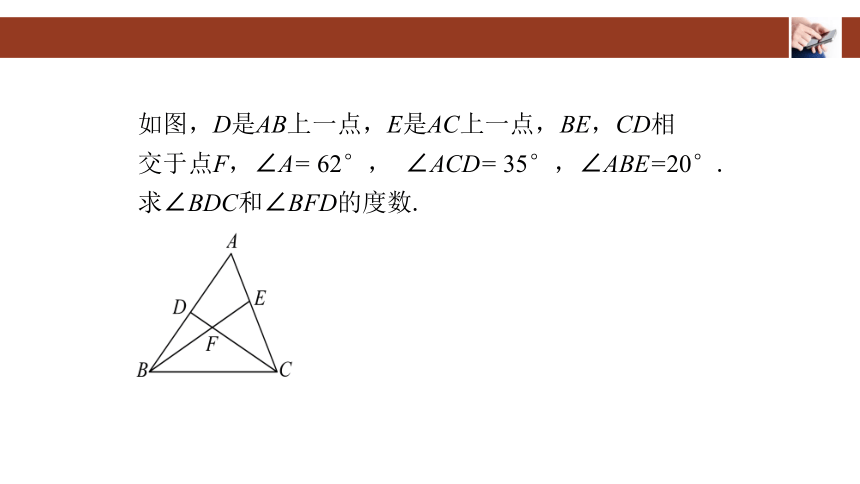
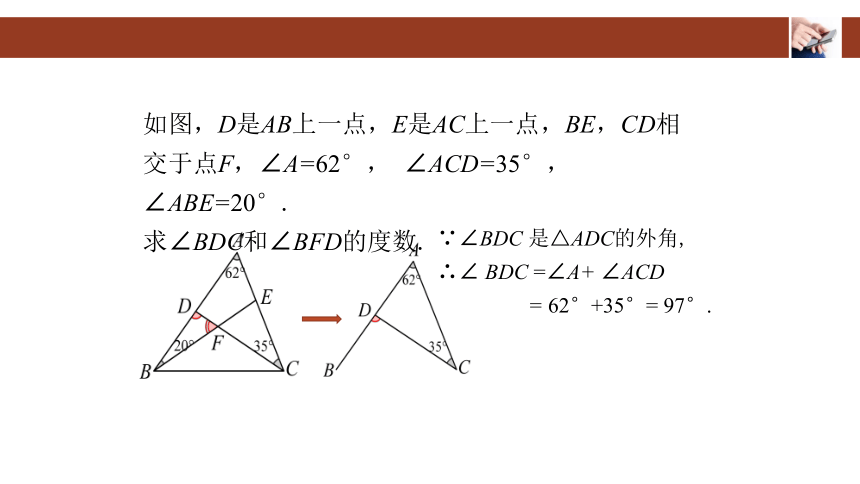
如图,D是AB上一点,E是AC上一点,BE,CD相
交于点F,∠A= 62°, ∠ACD= 35°,∠ABE=20°.
求∠BDC和∠BFD的度数.
如图,D是AB上一点,E是AC上一点,BE,CD相
交于点F,∠A=62°, ∠ACD=35°,∠ABE=20°.
求∠BDC和∠BFD的度数.
∵∠BDC 是△ADC的外角,
∴∠ BDC =∠A+ ∠ACD
= 62°+35°= 97°.
∵∠BDC 是△ADC的外角,
∴∠ BDC =∠A+ ∠ACD
= 62°+35°= 97°.
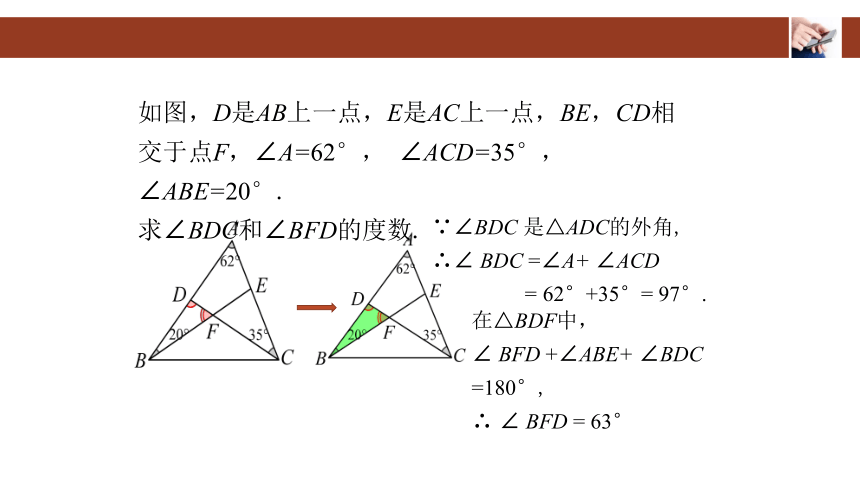
在△BDF中,
∠ BFD +∠ABE+ ∠BDC
=180°,
∴ ∠ BFD = 63°
如图,D是AB上一点,E是AC上一点,BE,CD相
交于点F,∠A=62°, ∠ACD=35°,∠ABE=20°.
求∠BDC和∠BFD的度数.
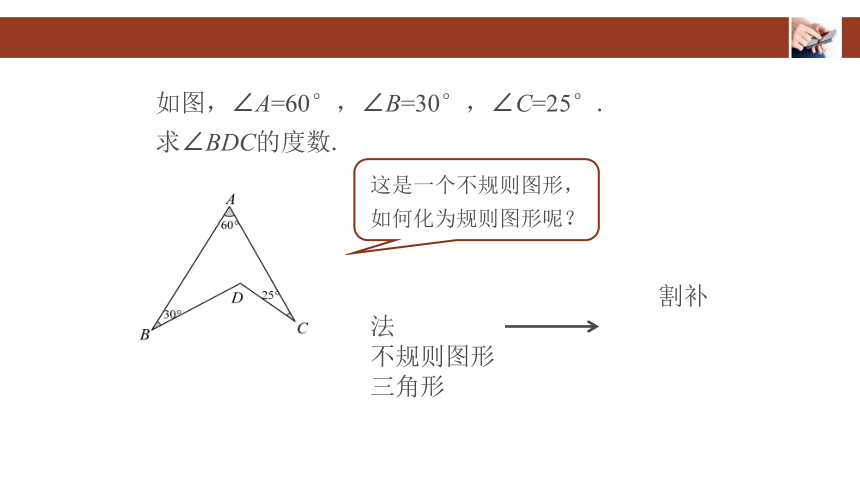
如图,∠A=60°,∠B=30°,∠C=25°.
求∠BDC的度数.
如图,∠A=60°,∠B=30°,∠C=25°.
求∠BDC的度数.
这是一个不规则图形,如何化为规则图形呢?
割补法
不规则图形 三角形
如图,∠A=60°,∠B=30°,∠C=25°.
求∠BDC的度数.
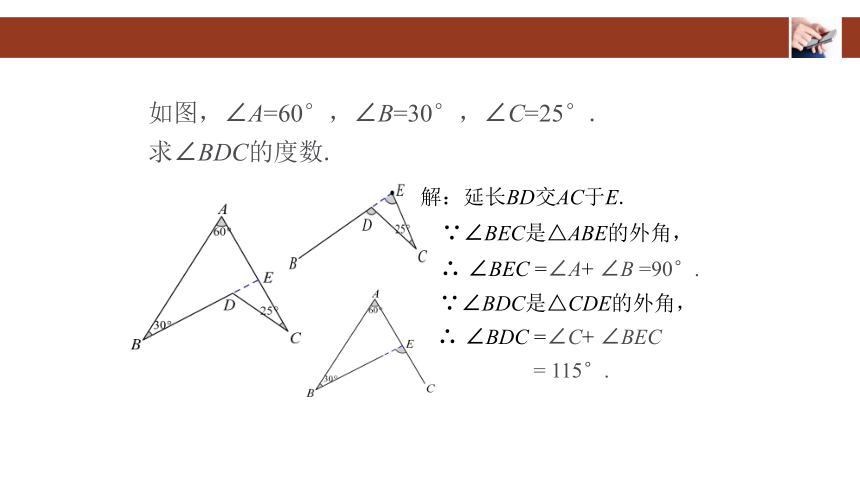
解:延长BD交AC于E.
∵∠BEC是△ABE的外角,
∴ ∠BEC =∠A+ ∠B =90°.
∵∠BDC是△CDE的外角,
∴ ∠BDC =∠C+ ∠BEC
= 115°.
如图,∠A=60°,∠B=30°,∠C=25°.
求∠BDC的度数.
解:作射线AD
∵∠3是△ABD的外角,
∴ ∠3 =∠1+ ∠B.
∵∠4是△ACD的外角,
∴ ∠4 =∠2+ ∠C.
∴ ∠3+ ∠4 =∠1+∠2+∠B+∠C.
如图,∠A=60°,∠B=30°,∠C=25°.
求∠BDC的度数.
解:
∵∠1+∠2 =∠BAC = 60°,
∠BDC = ∠3+ ∠4 ,
∴ ∠BDC =∠BAC+∠B+∠C
= 115°.
如图,∠A=60°,∠B=30°,∠C=25°.
求∠BDC的度数.
解:连接CB
在△ABC中,∠A +∠ABC+ ∠ACB=180°,
∴ ∠ABC+ ∠ACB=180°-∠A=120°.
在△DBC中,
∠BDC +∠1+ ∠2=180°,
∴ ∠BDC=180°-(∠1+∠2)=115°.
∴ ∠1+∠2=∠ABC-∠ABD+ ∠ACB-∠ACB
=120°-∠ABD-∠ACB=65°.
∠BDC=∠A+∠B+∠C
如图,把三角形纸片沿DE折叠.
(1)当点 A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律.
如图,把三角形纸片沿DE折叠.
(1)当点 A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律.
∵∠3=∠4,∠5=∠6,
∠1+∠3+∠4=180°,
∠4+∠6+∠A=180°,
∠2+∠5+∠6=180°,
∴∠1+∠2=2∠A.
如图,把三角形纸片沿DE折叠.
(1)当点 A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律.
∠1+∠2=2∠A
(2)当点 A落在四边形BCDE外部时,则∠A与∠1+∠2之间的这种数量关系还会保持不变吗?如果改变,新的规律又是什么呢?请试着找一找.
∠1+∠2=2∠A
(2)当点 A落在四边形BCDE外部时,则∠A与∠1+∠2之间的这种数量关系还会保持不变吗?如果改变,新的规律又是什么呢?请试着找一找.
(2)当点 A落在四边形BCDE外部时,则∠A与∠1+∠2之间的这种数量关系还会保持不变吗?如果改变,新的规律又是什么呢?请试着找一找.
(2)当点 A落在四边形BCDE外部时,则∠A与∠1+∠2之间的这种数量关系还会保持不变吗?如果改变,新的规律又是什么呢?请试着找一找.
∠2=∠3+∠A
(2)当点 A落在四边形BCDE外部时,则∠A与∠1+∠2之间的这种数量关系还会保持不变吗?如果改变,新的规律又是什么呢?请试着找一找.
∠2=∠3+∠A
∠3=∠1+∠A
(2)当点 A落在四边形BCDE外部时,则∠A与∠1+∠2之间的这种数量关系还会保持不变吗?如果改变,新的规律又是什么呢?请试着找一找.
∵∠2=∠3+∠A,
∠3=∠1+∠A,
∴∠2=∠1+2∠A.
∴∠2-∠1=2∠A.
(2)当点 A落在四边形BCDE外部时,则∠A与∠1+∠2之间的这种数量关系还会保持不变吗?如果改变,新的规律又是什么呢?请试着找一找.
∠2=∠A’AE+∠AA’E
∠1= ∠A’AD+∠AA’D
∴∠2-∠1=2∠A.
如图,△ABC中,∠B=∠C,∠BAD=40°,且∠ADE=∠AED,求∠CDE的度数.
如图,△ABC中,∠B=∠C,∠BAD=40°,且∠ADE=∠AED,求∠CDE的度数.
∠2是△CDE的外角,
∴ ∠2 =∠3 +∠C.
∠ADC是△ABD的外角,
∴ ∠1+ ∠3 =∠B +40°.
∠3是△CDE的内角,
观察∠3与其它角的关系
解:∵∠2是△CDE的外角,
∴∠2 =∠3 +∠C.
∵∠ADC是△ABD的外角,
∴∠ADC=∠B +∠BAD.
∴∠1+ ∠3 =∠B +40°.
∵∠1 =∠2 ,
∴∠3+ ∠3+ ∠C =∠B +40°.
∵∠B=∠C,
∴∠3 =20°.
如图,△ABC中,∠B=∠C,∠BAD=40°,且∠ADE=∠AED,求∠CDE的度数.
∴∠CDE= 20°.
∴y + (y x) = x+40°
2(y x) = 40°
y x = 20°.
解:设∠B=∠C = x,
∠ADE =∠AED = y,
则∠CDE=y x
课堂小结
与三角形的角有关的结论有哪些?
三角形的内角和等于180°;
三角形的一个外角等于与它不相邻的两个内角的和.
直角三角形的两个锐角互余;
课堂小结
在解决与三角形的角有关的问题时要注意哪些问题?
9. 如图,∠1=∠2,∠3=∠4,∠A=100°. 求x的值.
教科书 习题11.2 第17页
作 业
x
教科书 习题11.2 第17页
作 业
10. 如图,AB∥CD,∠BAE=∠DCE=45°. 填空:
∵AB∥CD,
∴∠1+45°+∠2+45°= .
∴∠1+∠2= .
∴∠E= .
11. 如图,CE是△ABC的外角∠ACD的平分线,且
CE交BA的延长线于点E. 求证∠BAC=∠B+2∠E.
教科书 习题11.2 第17页
作 业
同学们,再见!
复习回顾
与三角形的角有关的结论有哪些?
三角形的内角和等于180°;
三角形的一个外角等于与它不相邻的两个内角的和.
直角三角形的两个锐角互余;
∴∠2= 180°- 40°= 140°.
∴∠1=40°.
三角形内角和定理
∵∠2= 60°+ 80°= 140°,
∴∠1= 180° - ∠2 = 40°.
三角形外角性质
说出下列图形中∠1和∠2的度数:
说出下列图形中∠1和∠2的度数:
∠1=
∠2= 70°,∠ACD= 110°
∠1= 55°
说出下列图形中∠1和∠2的度数:
∠2= 140°
∠1= 90°- 40°= 50°
直角三角形的两个锐角互余
说出下列图形中∠1和∠2的度数:
∠1 = 80°
∠2 = 40°
如图,D是AB上一点,E是AC上一点,BE,CD相
交于点F,∠A= 62°, ∠ACD= 35°,∠ABE=20°.
求∠BDC和∠BFD的度数.
如图,D是AB上一点,E是AC上一点,BE,CD相
交于点F,∠A=62°, ∠ACD=35°,∠ABE=20°.
求∠BDC和∠BFD的度数.
∵∠BDC 是△ADC的外角,
∴∠ BDC =∠A+ ∠ACD
= 62°+35°= 97°.
∵∠BDC 是△ADC的外角,
∴∠ BDC =∠A+ ∠ACD
= 62°+35°= 97°.
在△BDF中,
∠ BFD +∠ABE+ ∠BDC
=180°,
∴ ∠ BFD = 63°
如图,D是AB上一点,E是AC上一点,BE,CD相
交于点F,∠A=62°, ∠ACD=35°,∠ABE=20°.
求∠BDC和∠BFD的度数.
如图,∠A=60°,∠B=30°,∠C=25°.
求∠BDC的度数.
如图,∠A=60°,∠B=30°,∠C=25°.
求∠BDC的度数.
这是一个不规则图形,如何化为规则图形呢?
割补法
不规则图形 三角形
如图,∠A=60°,∠B=30°,∠C=25°.
求∠BDC的度数.
解:延长BD交AC于E.
∵∠BEC是△ABE的外角,
∴ ∠BEC =∠A+ ∠B =90°.
∵∠BDC是△CDE的外角,
∴ ∠BDC =∠C+ ∠BEC
= 115°.
如图,∠A=60°,∠B=30°,∠C=25°.
求∠BDC的度数.
解:作射线AD
∵∠3是△ABD的外角,
∴ ∠3 =∠1+ ∠B.
∵∠4是△ACD的外角,
∴ ∠4 =∠2+ ∠C.
∴ ∠3+ ∠4 =∠1+∠2+∠B+∠C.
如图,∠A=60°,∠B=30°,∠C=25°.
求∠BDC的度数.
解:
∵∠1+∠2 =∠BAC = 60°,
∠BDC = ∠3+ ∠4 ,
∴ ∠BDC =∠BAC+∠B+∠C
= 115°.
如图,∠A=60°,∠B=30°,∠C=25°.
求∠BDC的度数.
解:连接CB
在△ABC中,∠A +∠ABC+ ∠ACB=180°,
∴ ∠ABC+ ∠ACB=180°-∠A=120°.
在△DBC中,
∠BDC +∠1+ ∠2=180°,
∴ ∠BDC=180°-(∠1+∠2)=115°.
∴ ∠1+∠2=∠ABC-∠ABD+ ∠ACB-∠ACB
=120°-∠ABD-∠ACB=65°.
∠BDC=∠A+∠B+∠C
如图,把三角形纸片沿DE折叠.
(1)当点 A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律.
如图,把三角形纸片沿DE折叠.
(1)当点 A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律.
∵∠3=∠4,∠5=∠6,
∠1+∠3+∠4=180°,
∠4+∠6+∠A=180°,
∠2+∠5+∠6=180°,
∴∠1+∠2=2∠A.
如图,把三角形纸片沿DE折叠.
(1)当点 A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律.
∠1+∠2=2∠A
(2)当点 A落在四边形BCDE外部时,则∠A与∠1+∠2之间的这种数量关系还会保持不变吗?如果改变,新的规律又是什么呢?请试着找一找.
∠1+∠2=2∠A
(2)当点 A落在四边形BCDE外部时,则∠A与∠1+∠2之间的这种数量关系还会保持不变吗?如果改变,新的规律又是什么呢?请试着找一找.
(2)当点 A落在四边形BCDE外部时,则∠A与∠1+∠2之间的这种数量关系还会保持不变吗?如果改变,新的规律又是什么呢?请试着找一找.
(2)当点 A落在四边形BCDE外部时,则∠A与∠1+∠2之间的这种数量关系还会保持不变吗?如果改变,新的规律又是什么呢?请试着找一找.
∠2=∠3+∠A
(2)当点 A落在四边形BCDE外部时,则∠A与∠1+∠2之间的这种数量关系还会保持不变吗?如果改变,新的规律又是什么呢?请试着找一找.
∠2=∠3+∠A
∠3=∠1+∠A
(2)当点 A落在四边形BCDE外部时,则∠A与∠1+∠2之间的这种数量关系还会保持不变吗?如果改变,新的规律又是什么呢?请试着找一找.
∵∠2=∠3+∠A,
∠3=∠1+∠A,
∴∠2=∠1+2∠A.
∴∠2-∠1=2∠A.
(2)当点 A落在四边形BCDE外部时,则∠A与∠1+∠2之间的这种数量关系还会保持不变吗?如果改变,新的规律又是什么呢?请试着找一找.
∠2=∠A’AE+∠AA’E
∠1= ∠A’AD+∠AA’D
∴∠2-∠1=2∠A.
如图,△ABC中,∠B=∠C,∠BAD=40°,且∠ADE=∠AED,求∠CDE的度数.
如图,△ABC中,∠B=∠C,∠BAD=40°,且∠ADE=∠AED,求∠CDE的度数.
∠2是△CDE的外角,
∴ ∠2 =∠3 +∠C.
∠ADC是△ABD的外角,
∴ ∠1+ ∠3 =∠B +40°.
∠3是△CDE的内角,
观察∠3与其它角的关系
解:∵∠2是△CDE的外角,
∴∠2 =∠3 +∠C.
∵∠ADC是△ABD的外角,
∴∠ADC=∠B +∠BAD.
∴∠1+ ∠3 =∠B +40°.
∵∠1 =∠2 ,
∴∠3+ ∠3+ ∠C =∠B +40°.
∵∠B=∠C,
∴∠3 =20°.
如图,△ABC中,∠B=∠C,∠BAD=40°,且∠ADE=∠AED,求∠CDE的度数.
∴∠CDE= 20°.
∴y + (y x) = x+40°
2(y x) = 40°
y x = 20°.
解:设∠B=∠C = x,
∠ADE =∠AED = y,
则∠CDE=y x
课堂小结
与三角形的角有关的结论有哪些?
三角形的内角和等于180°;
三角形的一个外角等于与它不相邻的两个内角的和.
直角三角形的两个锐角互余;
课堂小结
在解决与三角形的角有关的问题时要注意哪些问题?
9. 如图,∠1=∠2,∠3=∠4,∠A=100°. 求x的值.
教科书 习题11.2 第17页
作 业
x
教科书 习题11.2 第17页
作 业
10. 如图,AB∥CD,∠BAE=∠DCE=45°. 填空:
∵AB∥CD,
∴∠1+45°+∠2+45°= .
∴∠1+∠2= .
∴∠E= .
11. 如图,CE是△ABC的外角∠ACD的平分线,且
CE交BA的延长线于点E. 求证∠BAC=∠B+2∠E.
教科书 习题11.2 第17页
作 业
同学们,再见!
