人教版八年级数学上册11.1.1_三角形的边课件(23张)
文档属性
| 名称 | 人教版八年级数学上册11.1.1_三角形的边课件(23张) |  | |
| 格式 | ppt | ||
| 文件大小 | 602.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:21:22 | ||
图片预览



文档简介
第十一章 三角形
11.1 与三角形有关的线段
11.1.1 三角形的边
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
A
B
C
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
注意:1.不在同一条直线上. 2.首尾顺次相接.
注意:表示三角形时,字母没有先后顺序.即:可以记作△ABC,也可记作△ACB.
2.三角形的表示:
三角形用符号“△”表示,如上图的三角形,记作“△ABC”,读作“三角形ABC”.
1.三角形的定义:
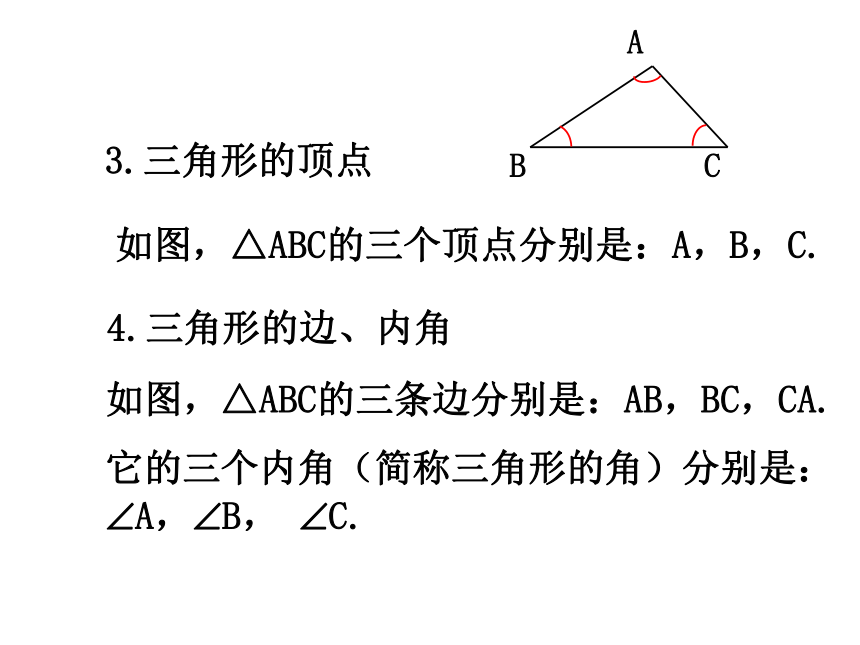
如图,△ABC的三个顶点分别是:A,B,C.
3.三角形的顶点
如图,△ABC的三条边分别是:AB,BC,CA.
它的三个内角(简称三角形的角)分别是: ?A,?B, ?C.
A
B
C
4.三角形的边、内角
A
B
C
a
b
c
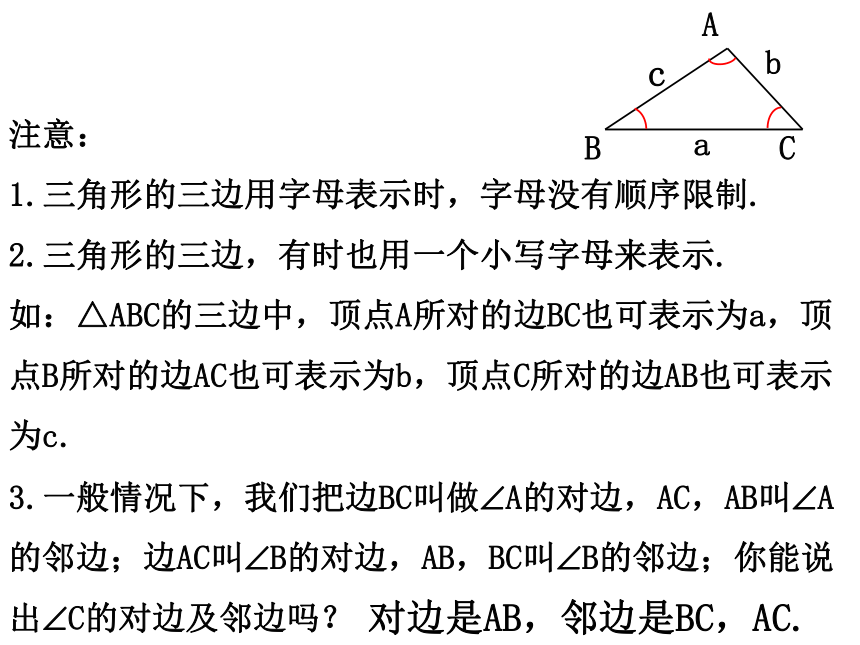
注意:
1.三角形的三边用字母表示时,字母没有顺序限制.
2.三角形的三边,有时也用一个小写字母来表示.
如:△ABC的三边中,顶点A所对的边BC也可表示为a,顶点B所对的边AC也可表示为b,顶点C所对的边AB也可表示为c.
3.一般情况下,我们把边BC叫做?A的对边,AC,AB叫?A的邻边;边AC叫?B的对边,AB,BC叫?B的邻边;你能说出?C的对边及邻边吗?
对边是AB,邻边是BC,AC.
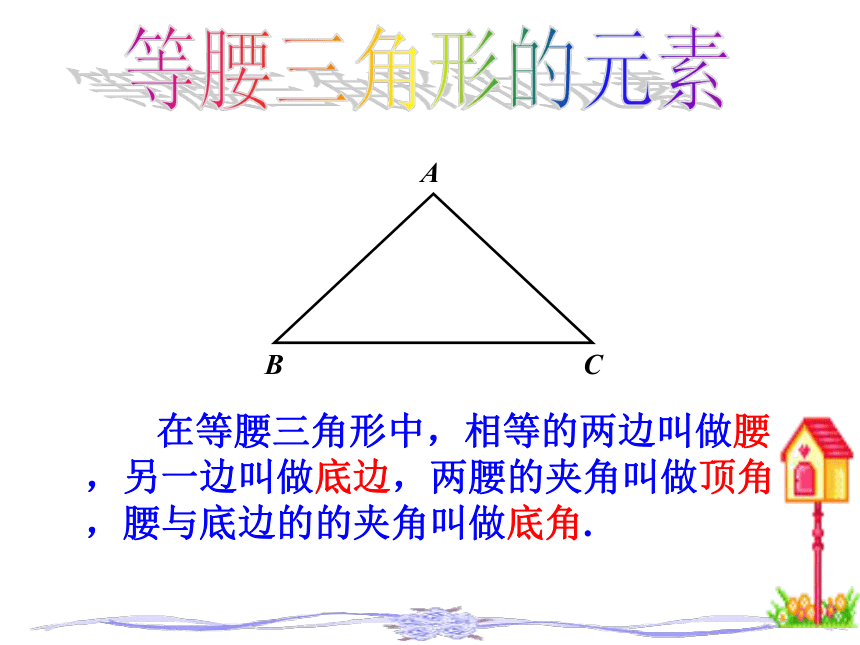
在等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰与底边的的夹角叫做底角.
等腰三角形的元素
A
B
C
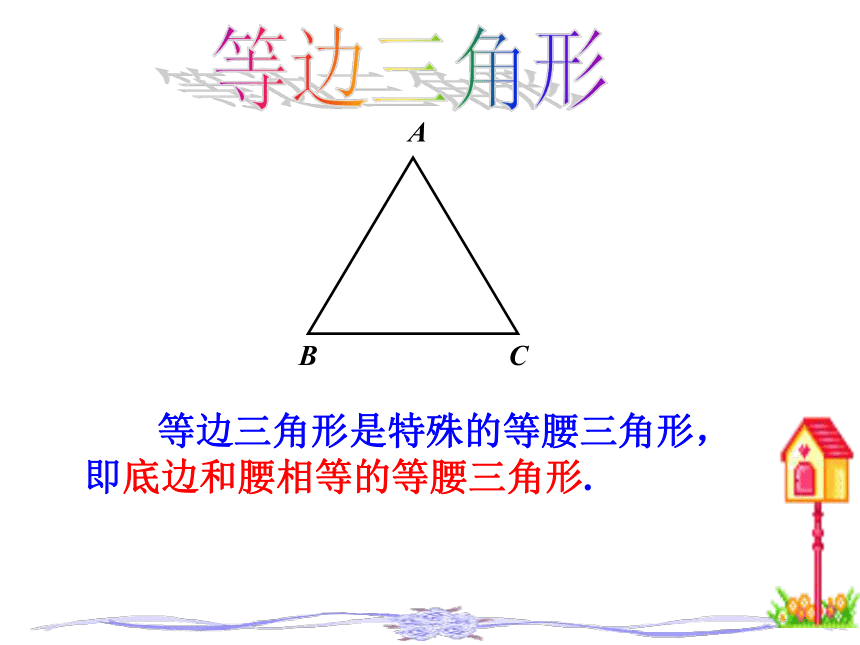
等边三角形
A
B
C
等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形.
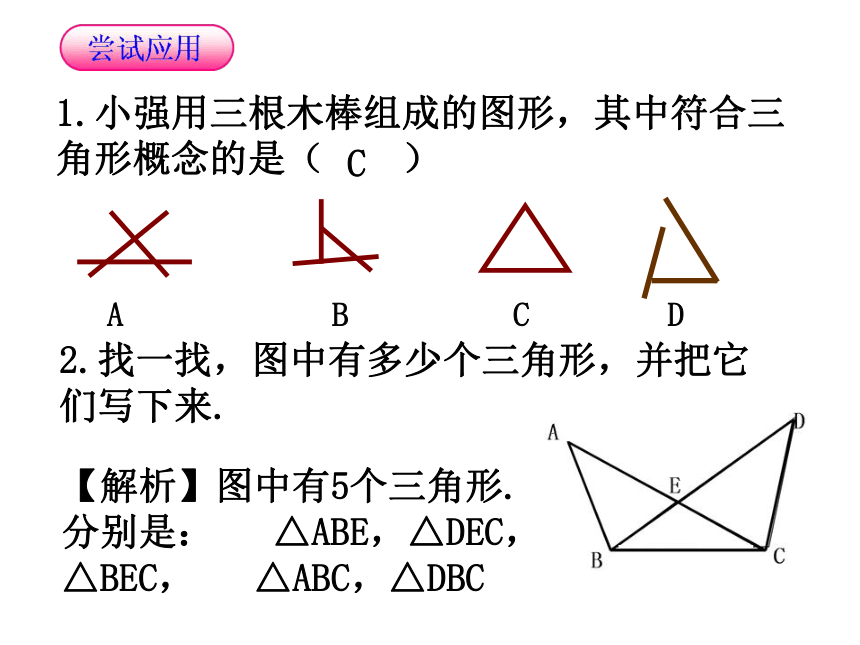
1.小强用三根木棒组成的图形,其中符合三角形概念的是( )
B
A
C
C
2.找一找,图中有多少个三角形,并把它们写下来.
【解析】图中有5个三角形.分别是: △ABE,△DEC, △BEC, △ABC,△DBC
D
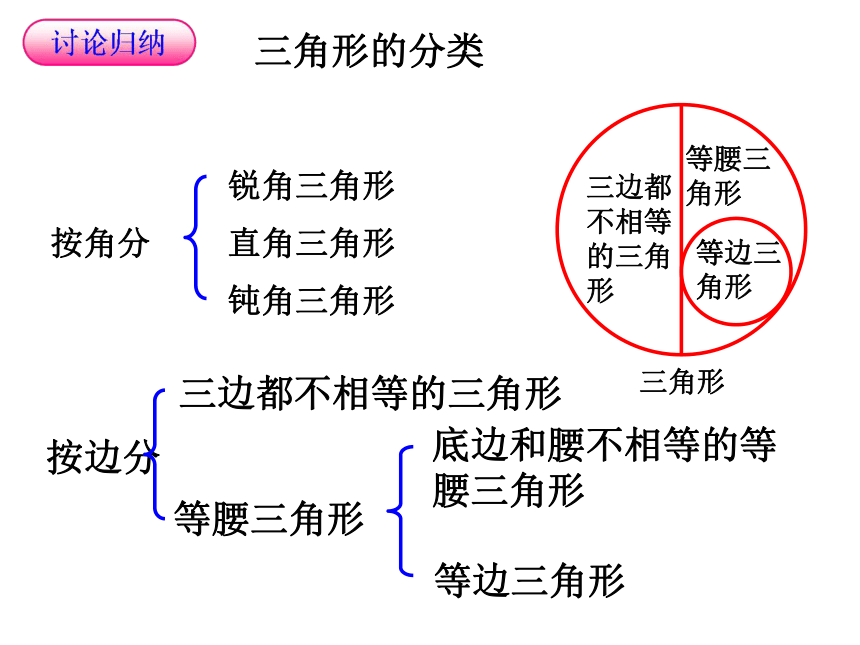
三角形
按角分
锐角三角形
直角三角形
钝角三角形
按边分
三边都不相等的三角形
三角形的分类
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
三边都不相等的三角形
等腰三角形
等边三角形
任意画一个△ABC,假设一条小虫从点B出发,沿三角形的边爬到点C,它有几条线路可以选择?各条线路的长一样吗?
探究
A
B
C
AB+AC
BC
>
想一想,为什么?
两点的所有连线中,线段最短.
同理:AC+BC>AB,AB+BC>AC.
探 究
A
B
C
AB+AC>BC, ①
AC+BC>AB, ②
AB+BC>AC. ③
AC-AB<BC, ④
BC-AC<AB, ⑤
BC-AB<AC. ⑥
问:式子④⑤⑥成立吗?
成立
三角形的三边关系:
三角形两边之和大于第三边;
三角形两边之差小于第三边.
下列长度的三条线段能否组成三角形?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
小窍门:用较短的两条线段之和与最长的线段比较,若和大,能组成三角形,反之,则不能.
【例】若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长.
【解析】设第三边的长为x,根据两边之和大于第三边得:x<2+7即x<9.
根据两边之差小于第三边得:x>7-2即x>5.
所以x的值大于5小于9,又因为它是奇数,
所以x只能取7.
答:第三边的长为7.
例 用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边长是多少?
(2)能围成有一边长为4cm的等腰三角形吗?为什么?
(1)解:设底边长为x cm,腰长2x cm.
x+2x+2x=18
解得 x=3.6
∴三边长分别为3.6cm、7.2cm、7.2cm.
例 用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边长是多少?
(2)能围成有一边长为4cm的等腰三角形吗?为什么?
(2)解:①如果4cm长的边为底边,那么设腰长为x cm.
4+2x=18
解得 x=7
则底边的取值范围为7-7<x<7+7
∴三边长分别为4cm、7cm、7cm
②如果4cm长的边为腰,那么设底边长为y cm.
2×4+y=18
解得 y=10
又∵底边的取值范围为4-4<y<4+4
∴不能围成腰长为4cm的等腰三角形
1.下列每组数分别是三根小木棒的长度,用它们能摆成三角形吗?实际摆一摆,验证你的结论.
(1)8 cm, 7 cm, 15 cm
(2)13 cm, 12 cm, 20 cm
(3)5 cm, 5 cm, 11 cm
2.现有长度分别为1 cm,2 cm,3 cm,4 cm,5 cm的五条线段,从其中选三条线段为边可以构成 个不同的三角形.
(2)能摆成三角形
3
【跟踪训练】
3.如果三角形的两边长分别是2和4,且第三边是奇数,那么第三边长为 .若第三边为偶数,那么三角形的周长为 .
3或5
10
4.有两根长度分别为5 cm和8 cm的木棒,用长度为2 cm的木棒与它们能摆成三角形吗?为什么?长度为13 cm的木棒呢?
解:取长度为2 cm的木棒时,由于2+5=7 < 8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.
取长度为13 cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
1. 在如图所示的图形中,三角形的个数共有( )
A.1个 B.2个
C. 3个 D.4个
A
B
C
D
图中有△ABC,△ABD,△ACD.
C
2. 下列长度的三条线段,不能组成三角形的是( )
A.3,8,4 B.4,9,6 C.15,20,8 D.9,15,8
3.若某三角形的两边长分别为3和4,则下列长度的线段能作为其第三边的是( )
A.1 B.5 C.7 D.9
B
A
4.若△ABC的三边为a,b,c,则化简
︱a+b-c︱+︱b-a-c︱的结果是( ).
A. 2a-2b B.2a+2b+2c
C. 2a D. 2a-2c
C
5.已知一个三角形的三边a=7,b=3,第三边c是一个正整数,满足这些条件的三角形共有 种,当c= 时,三角形的周长最长.
5
9
概念
三角形
分类
表示方法
三边关系
通过本课时的学习,需要我们掌握
11.1 与三角形有关的线段
11.1.1 三角形的边
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
A
B
C
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
注意:1.不在同一条直线上. 2.首尾顺次相接.
注意:表示三角形时,字母没有先后顺序.即:可以记作△ABC,也可记作△ACB.
2.三角形的表示:
三角形用符号“△”表示,如上图的三角形,记作“△ABC”,读作“三角形ABC”.
1.三角形的定义:
如图,△ABC的三个顶点分别是:A,B,C.
3.三角形的顶点
如图,△ABC的三条边分别是:AB,BC,CA.
它的三个内角(简称三角形的角)分别是: ?A,?B, ?C.
A
B
C
4.三角形的边、内角
A
B
C
a
b
c
注意:
1.三角形的三边用字母表示时,字母没有顺序限制.
2.三角形的三边,有时也用一个小写字母来表示.
如:△ABC的三边中,顶点A所对的边BC也可表示为a,顶点B所对的边AC也可表示为b,顶点C所对的边AB也可表示为c.
3.一般情况下,我们把边BC叫做?A的对边,AC,AB叫?A的邻边;边AC叫?B的对边,AB,BC叫?B的邻边;你能说出?C的对边及邻边吗?
对边是AB,邻边是BC,AC.
在等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰与底边的的夹角叫做底角.
等腰三角形的元素
A
B
C
等边三角形
A
B
C
等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形.
1.小强用三根木棒组成的图形,其中符合三角形概念的是( )
B
A
C
C
2.找一找,图中有多少个三角形,并把它们写下来.
【解析】图中有5个三角形.分别是: △ABE,△DEC, △BEC, △ABC,△DBC
D
三角形
按角分
锐角三角形
直角三角形
钝角三角形
按边分
三边都不相等的三角形
三角形的分类
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
三边都不相等的三角形
等腰三角形
等边三角形
任意画一个△ABC,假设一条小虫从点B出发,沿三角形的边爬到点C,它有几条线路可以选择?各条线路的长一样吗?
探究
A
B
C
AB+AC
BC
>
想一想,为什么?
两点的所有连线中,线段最短.
同理:AC+BC>AB,AB+BC>AC.
探 究
A
B
C
AB+AC>BC, ①
AC+BC>AB, ②
AB+BC>AC. ③
AC-AB<BC, ④
BC-AC<AB, ⑤
BC-AB<AC. ⑥
问:式子④⑤⑥成立吗?
成立
三角形的三边关系:
三角形两边之和大于第三边;
三角形两边之差小于第三边.
下列长度的三条线段能否组成三角形?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
小窍门:用较短的两条线段之和与最长的线段比较,若和大,能组成三角形,反之,则不能.
【例】若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长.
【解析】设第三边的长为x,根据两边之和大于第三边得:x<2+7即x<9.
根据两边之差小于第三边得:x>7-2即x>5.
所以x的值大于5小于9,又因为它是奇数,
所以x只能取7.
答:第三边的长为7.
例 用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边长是多少?
(2)能围成有一边长为4cm的等腰三角形吗?为什么?
(1)解:设底边长为x cm,腰长2x cm.
x+2x+2x=18
解得 x=3.6
∴三边长分别为3.6cm、7.2cm、7.2cm.
例 用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边长是多少?
(2)能围成有一边长为4cm的等腰三角形吗?为什么?
(2)解:①如果4cm长的边为底边,那么设腰长为x cm.
4+2x=18
解得 x=7
则底边的取值范围为7-7<x<7+7
∴三边长分别为4cm、7cm、7cm
②如果4cm长的边为腰,那么设底边长为y cm.
2×4+y=18
解得 y=10
又∵底边的取值范围为4-4<y<4+4
∴不能围成腰长为4cm的等腰三角形
1.下列每组数分别是三根小木棒的长度,用它们能摆成三角形吗?实际摆一摆,验证你的结论.
(1)8 cm, 7 cm, 15 cm
(2)13 cm, 12 cm, 20 cm
(3)5 cm, 5 cm, 11 cm
2.现有长度分别为1 cm,2 cm,3 cm,4 cm,5 cm的五条线段,从其中选三条线段为边可以构成 个不同的三角形.
(2)能摆成三角形
3
【跟踪训练】
3.如果三角形的两边长分别是2和4,且第三边是奇数,那么第三边长为 .若第三边为偶数,那么三角形的周长为 .
3或5
10
4.有两根长度分别为5 cm和8 cm的木棒,用长度为2 cm的木棒与它们能摆成三角形吗?为什么?长度为13 cm的木棒呢?
解:取长度为2 cm的木棒时,由于2+5=7 < 8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.
取长度为13 cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
1. 在如图所示的图形中,三角形的个数共有( )
A.1个 B.2个
C. 3个 D.4个
A
B
C
D
图中有△ABC,△ABD,△ACD.
C
2. 下列长度的三条线段,不能组成三角形的是( )
A.3,8,4 B.4,9,6 C.15,20,8 D.9,15,8
3.若某三角形的两边长分别为3和4,则下列长度的线段能作为其第三边的是( )
A.1 B.5 C.7 D.9
B
A
4.若△ABC的三边为a,b,c,则化简
︱a+b-c︱+︱b-a-c︱的结果是( ).
A. 2a-2b B.2a+2b+2c
C. 2a D. 2a-2c
C
5.已知一个三角形的三边a=7,b=3,第三边c是一个正整数,满足这些条件的三角形共有 种,当c= 时,三角形的周长最长.
5
9
概念
三角形
分类
表示方法
三边关系
通过本课时的学习,需要我们掌握
