人教版八年级数学上册课件:12.2.2三角形全等的判定(SAS)(26张)
文档属性
| 名称 | 人教版八年级数学上册课件:12.2.2三角形全等的判定(SAS)(26张) |  | |
| 格式 | ppt | ||
| 文件大小 | 332.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-12 21:23:02 | ||
图片预览





文档简介
12.2.2 三角形全等的判定
(SAS)
我们学过哪几种判定三角形全等的方法?
1、全等三角形概念:三条边对应相等,三个角对应相等。
2、全等三角形判定条件(一)
三边对应相等的两个三角形全等。
简称“边边边”或“SSS”
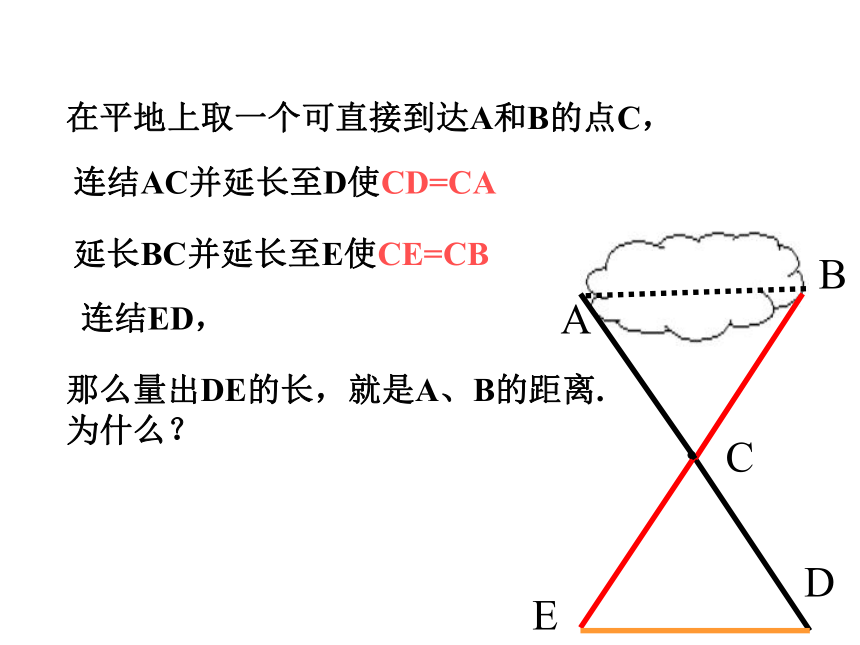
问题:如图有一池塘。要测池塘两端A、B的距离,可无法直接达到,因此这两点的距离无法直接量出。你能想出办法来吗?
A
B
A
B
C
E
D
在平地上取一个可直接到达A和B的点C,
连结AC并延长至D使CD=CA
延长BC并延长至E使CE=CB
连结ED,
那么量出DE的长,就是A、B的距离.为什么?
1. 画∠MA′N = ∠A
2. 在射线 A M ,A N 上分别取 A ′B ′ = AB ,
A ′C ′= AC .
3. 连接 B ′C ′ ,得 ?A ′B ′C ′.
已知△ABC是任意一个三角形,
画△A ′B′C ′使∠A ′ = ∠A, A ′B ′ =AB, A ′ C ′ =AC.
画法:
边角边公理
有两边和它们的夹角对应相等的
两个三角形全等.
可以简写成 “边角边” 或“ SAS ”
S ——边 A——角
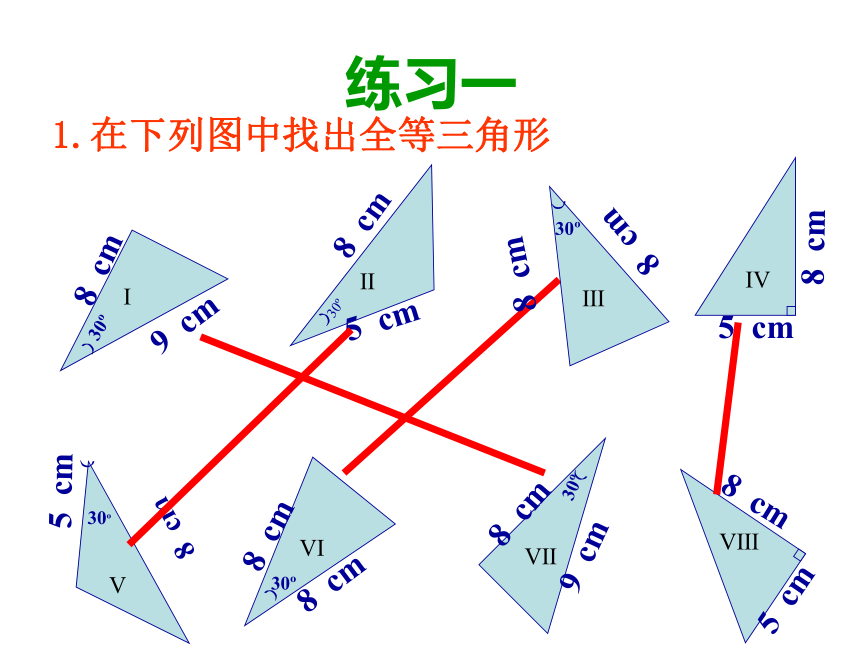
1.在下列图中找出全等三角形
Ⅰ
?
30?
8 cm
9 cm
Ⅵ
?
30?
8 cm
8 cm
Ⅳ
Ⅳ
8 cm
5 cm
Ⅱ
30?
?
8 cm
5 cm
Ⅴ
30?
8 cm
?
5 cm
Ⅷ
8 cm
5 cm
?
30?
8 cm
9 cm
Ⅶ
Ⅲ
?
30?
8 cm
8 cm
Ⅲ
练习一
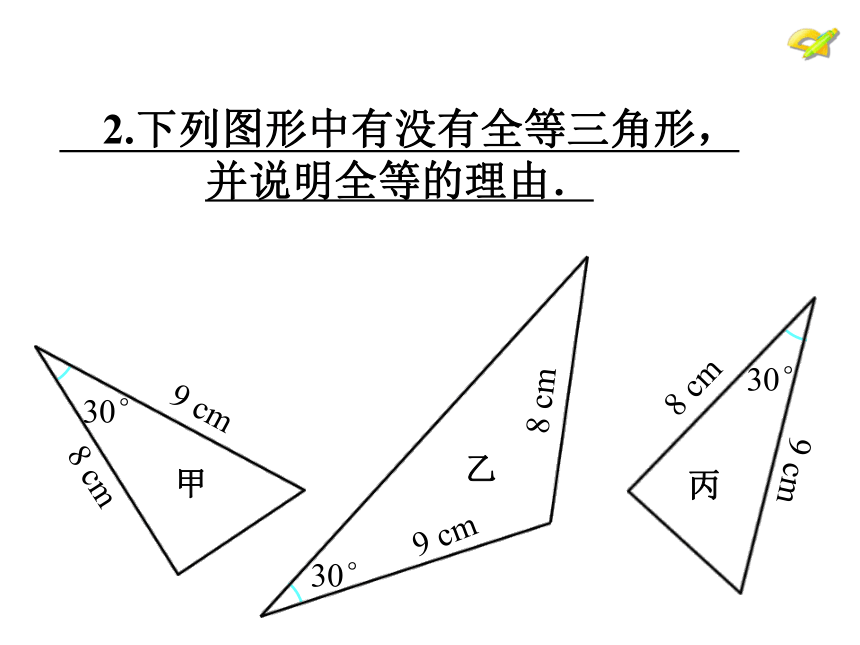
2.下列图形中有没有全等三角形,并说明全等的理由.
甲
8 cm
9 cm
丙
8 cm
9 cm
8 cm
9 cm
乙
30°
30°
30°
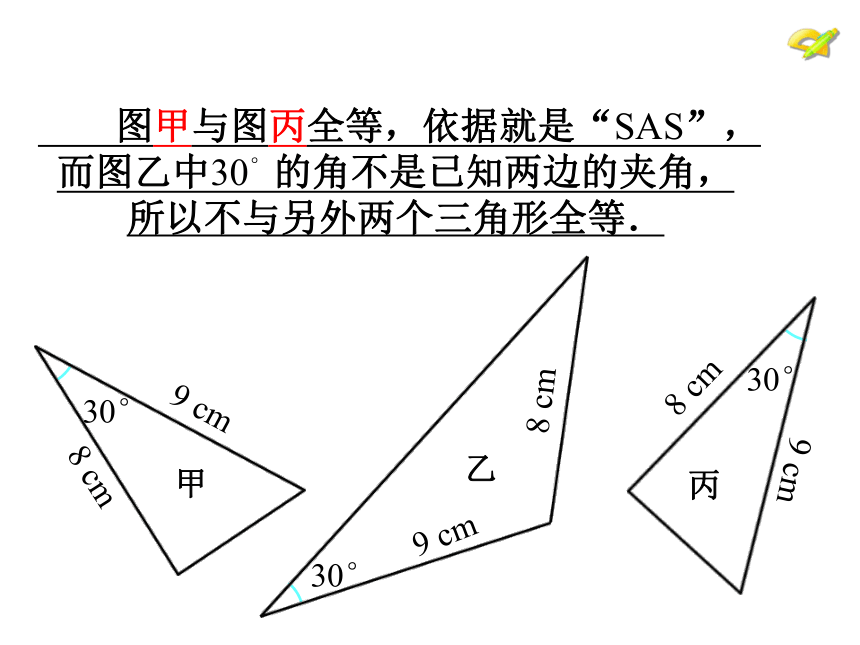
图甲与图丙全等,依据就是“SAS”,而图乙中30°的角不是已知两边的夹角,所以不与另外两个三角形全等.
甲
8 cm
9 cm
丙
8 cm
9 cm
8 cm
9 cm
乙
30°
30°
30°
利用今天所学“边角边”知识,带黑色的那块.因
为它完整地保留了两边及其夹角,
一个三角形两条边的长度和夹角的
大小确定了,这个三角形的形状、
大小就确定下来了.
应用“SAS”判定方法,解决简单实际问题
3. 某同学不小心把一块三角形的玻璃从两个顶点处打碎成两块(如图),现要到玻璃店去配一块完全一样的玻璃.请问如果只准带一块碎片,应该带哪一块去,能试着说明理由吗?
4.在下列推理中填写需要补充的条件,使结论成立:
(1)如图,在△AOB和△DOC中
AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC( )
∠ AOB
∠ DOC
对顶角相等
SAS
C
A
B
D
O
5.已知:如图,AC=AD ,∠CAB=∠DAB.
求证: △ACB ≌ △ADB.
A
B
C
D
证明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?
还要一条边
隐含条件:公共边,公共角,对顶角
已知: 如图,AC=AD ,∠CAB=∠DAB.
求证: △ACB ≌ △ADB.
A
B
C
D
证明:
在△ACB 和 △ADB中
AC = A D (已知)
∠CAB=∠DAB(已知)
A B = A B (公共边)
∴△ACB≌△ADB
(SAS)
A
B
C
E
D
在平地上取一个可直接到达A和B的点C,
连结AC并延长至D使CD=CA
延长BC并延长至E使CE=CB
连结ED,
那么量出DE的长,就是A、B的距离.为什么?
回到初始问题???
证明三角形全等的步骤:
?1.写出在哪两个三角形中证明全等。
(注意把表示对应顶点的字母写在对应的位置上).
?2.按边、角、边的顺序列出三个条件,用大括号合在一起.
?3.证明全等后要有推理的依据.
6.已知:如图,AB =AC AD = AE .求证:△ ABE≌ △ ACD.
证明: 在△ABE 和△ACD 中,
AB = AC(已知),
AE = AD(已知),
∠A = ∠A(公共角),
∴ △ ABE ≌ △ ACD(SAS).
B
E
A
C
D
如图,在△ABC 和△ABD 中,
AB =AB,AC = AD,∠B =∠B,
但△ABC 和△ABD 不全等.
探索“SSA”能否识别两三角形全等
7. 两边一角分别相等包括“两边夹角”和
“两边及其中一边的对角”分别相等两种情况,前面已
探索出“SAS”判定三角形全等的方法,那么由“SSA”
的条件能判定两个三角形全等吗?
A
B
C
D
画△ABC 和△DEF,使∠B =∠E =30°, AB =DE
=5 cm ,AC =DF =3 cm .观察所得的两个三角形是否全
等?
?
两边和其中一边的对角这三个条件无法唯一确定三
角形的形状,所以不能保证两个三角形全等.因此,
△ABC 和△DEF 不一定全等.
探索“SSA”能否识别两三角形全等
课堂小结
1.边角边公理:有两边和它们的______对应相等的 两个三角形全等(SAS)
夹角
2.边角边公理的应用中所用到的数学方法:
证明线段(或角相等) 证明线段(或角)所在的两个三角形全等.
转化
1.若AB=AC,则添加什么条件可得△ABD≌ △ACD?
△ABD≌ △ACD
AD=AD
AB=AC
A
B
D
C
∠BAD= ∠CAD
S
A
S
拓展
2.已知如图,点D 在AB上,点E在AC上,BE与CD交于点O,
△ABE≌ △ACD
S
A
S
AB=AC
∠A= ∠ A
AE=AD
要证△ABE≌ △ACD需添加什么条件?
B
E
A
A
C
D
O
2.已知如图,点D 在AB上,点E在AC上,BE与CD交于点O,
S
A
S
OB=OC
∠BOD= ∠ COE
OD=OE
要证△BOD≌ △COE需添加什么条件?
B
E
A
A
C
D
O
△BOD≌ △COE
3.如图,要证△ACB≌ △ADB ,至少选用哪些条件才可以?
A
B
C
D
△ACB≌ △ADB
S
A
S
证得△ACB≌ △ADB
AB=AB
∠CAB= ∠ DAB
AC=AD
3.如图,要证△ACB≌ △ADB ,至少选用哪些条件可
A
B
C
D
△ACB≌ △ADB
S
A
S
证得△ACB≌ △ADB
AB=AB
∠CBA= ∠ DBA
BC=BD
教科书习题12.2第2、3、10题.
Over!
(SAS)
我们学过哪几种判定三角形全等的方法?
1、全等三角形概念:三条边对应相等,三个角对应相等。
2、全等三角形判定条件(一)
三边对应相等的两个三角形全等。
简称“边边边”或“SSS”
问题:如图有一池塘。要测池塘两端A、B的距离,可无法直接达到,因此这两点的距离无法直接量出。你能想出办法来吗?
A
B
A
B
C
E
D
在平地上取一个可直接到达A和B的点C,
连结AC并延长至D使CD=CA
延长BC并延长至E使CE=CB
连结ED,
那么量出DE的长,就是A、B的距离.为什么?
1. 画∠MA′N = ∠A
2. 在射线 A M ,A N 上分别取 A ′B ′ = AB ,
A ′C ′= AC .
3. 连接 B ′C ′ ,得 ?A ′B ′C ′.
已知△ABC是任意一个三角形,
画△A ′B′C ′使∠A ′ = ∠A, A ′B ′ =AB, A ′ C ′ =AC.
画法:
边角边公理
有两边和它们的夹角对应相等的
两个三角形全等.
可以简写成 “边角边” 或“ SAS ”
S ——边 A——角
1.在下列图中找出全等三角形
Ⅰ
?
30?
8 cm
9 cm
Ⅵ
?
30?
8 cm
8 cm
Ⅳ
Ⅳ
8 cm
5 cm
Ⅱ
30?
?
8 cm
5 cm
Ⅴ
30?
8 cm
?
5 cm
Ⅷ
8 cm
5 cm
?
30?
8 cm
9 cm
Ⅶ
Ⅲ
?
30?
8 cm
8 cm
Ⅲ
练习一
2.下列图形中有没有全等三角形,并说明全等的理由.
甲
8 cm
9 cm
丙
8 cm
9 cm
8 cm
9 cm
乙
30°
30°
30°
图甲与图丙全等,依据就是“SAS”,而图乙中30°的角不是已知两边的夹角,所以不与另外两个三角形全等.
甲
8 cm
9 cm
丙
8 cm
9 cm
8 cm
9 cm
乙
30°
30°
30°
利用今天所学“边角边”知识,带黑色的那块.因
为它完整地保留了两边及其夹角,
一个三角形两条边的长度和夹角的
大小确定了,这个三角形的形状、
大小就确定下来了.
应用“SAS”判定方法,解决简单实际问题
3. 某同学不小心把一块三角形的玻璃从两个顶点处打碎成两块(如图),现要到玻璃店去配一块完全一样的玻璃.请问如果只准带一块碎片,应该带哪一块去,能试着说明理由吗?
4.在下列推理中填写需要补充的条件,使结论成立:
(1)如图,在△AOB和△DOC中
AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC( )
∠ AOB
∠ DOC
对顶角相等
SAS
C
A
B
D
O
5.已知:如图,AC=AD ,∠CAB=∠DAB.
求证: △ACB ≌ △ADB.
A
B
C
D
证明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?
还要一条边
隐含条件:公共边,公共角,对顶角
已知: 如图,AC=AD ,∠CAB=∠DAB.
求证: △ACB ≌ △ADB.
A
B
C
D
证明:
在△ACB 和 △ADB中
AC = A D (已知)
∠CAB=∠DAB(已知)
A B = A B (公共边)
∴△ACB≌△ADB
(SAS)
A
B
C
E
D
在平地上取一个可直接到达A和B的点C,
连结AC并延长至D使CD=CA
延长BC并延长至E使CE=CB
连结ED,
那么量出DE的长,就是A、B的距离.为什么?
回到初始问题???
证明三角形全等的步骤:
?1.写出在哪两个三角形中证明全等。
(注意把表示对应顶点的字母写在对应的位置上).
?2.按边、角、边的顺序列出三个条件,用大括号合在一起.
?3.证明全等后要有推理的依据.
6.已知:如图,AB =AC AD = AE .求证:△ ABE≌ △ ACD.
证明: 在△ABE 和△ACD 中,
AB = AC(已知),
AE = AD(已知),
∠A = ∠A(公共角),
∴ △ ABE ≌ △ ACD(SAS).
B
E
A
C
D
如图,在△ABC 和△ABD 中,
AB =AB,AC = AD,∠B =∠B,
但△ABC 和△ABD 不全等.
探索“SSA”能否识别两三角形全等
7. 两边一角分别相等包括“两边夹角”和
“两边及其中一边的对角”分别相等两种情况,前面已
探索出“SAS”判定三角形全等的方法,那么由“SSA”
的条件能判定两个三角形全等吗?
A
B
C
D
画△ABC 和△DEF,使∠B =∠E =30°, AB =DE
=5 cm ,AC =DF =3 cm .观察所得的两个三角形是否全
等?
?
两边和其中一边的对角这三个条件无法唯一确定三
角形的形状,所以不能保证两个三角形全等.因此,
△ABC 和△DEF 不一定全等.
探索“SSA”能否识别两三角形全等
课堂小结
1.边角边公理:有两边和它们的______对应相等的 两个三角形全等(SAS)
夹角
2.边角边公理的应用中所用到的数学方法:
证明线段(或角相等) 证明线段(或角)所在的两个三角形全等.
转化
1.若AB=AC,则添加什么条件可得△ABD≌ △ACD?
△ABD≌ △ACD
AD=AD
AB=AC
A
B
D
C
∠BAD= ∠CAD
S
A
S
拓展
2.已知如图,点D 在AB上,点E在AC上,BE与CD交于点O,
△ABE≌ △ACD
S
A
S
AB=AC
∠A= ∠ A
AE=AD
要证△ABE≌ △ACD需添加什么条件?
B
E
A
A
C
D
O
2.已知如图,点D 在AB上,点E在AC上,BE与CD交于点O,
S
A
S
OB=OC
∠BOD= ∠ COE
OD=OE
要证△BOD≌ △COE需添加什么条件?
B
E
A
A
C
D
O
△BOD≌ △COE
3.如图,要证△ACB≌ △ADB ,至少选用哪些条件才可以?
A
B
C
D
△ACB≌ △ADB
S
A
S
证得△ACB≌ △ADB
AB=AB
∠CAB= ∠ DAB
AC=AD
3.如图,要证△ACB≌ △ADB ,至少选用哪些条件可
A
B
C
D
△ACB≌ △ADB
S
A
S
证得△ACB≌ △ADB
AB=AB
∠CBA= ∠ DBA
BC=BD
教科书习题12.2第2、3、10题.
Over!
