人教版八年级数学下册 19.2.2.3待定系数课件(共17张ppt)
文档属性
| 名称 | 人教版八年级数学下册 19.2.2.3待定系数课件(共17张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 346.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-11 21:10:23 | ||
图片预览





文档简介
19.2.2待定系数法
学习目标:
1.掌握待定系数法,归纳用其方法求一次函数解析式的步骤。
2.具体感知数形结合思想在一次函数中的应用.
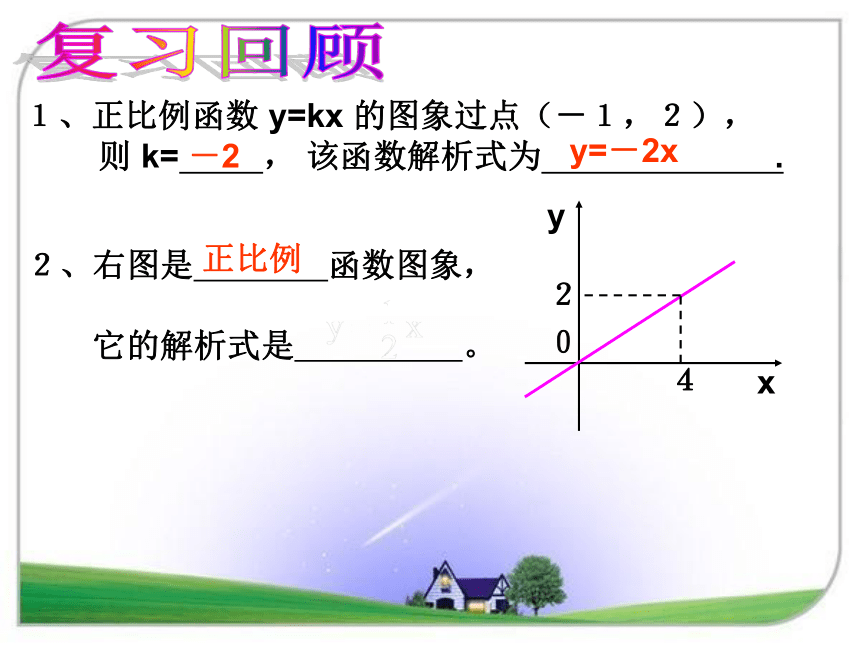
1、正比例函数 y=kx 的图象过点(-1,2),
则 k= , 该函数解析式为 .
2、右图是 函数图象,
它的解析式是 。
-2
y=-2x
0
2
4
y
x
正比例
复习回顾
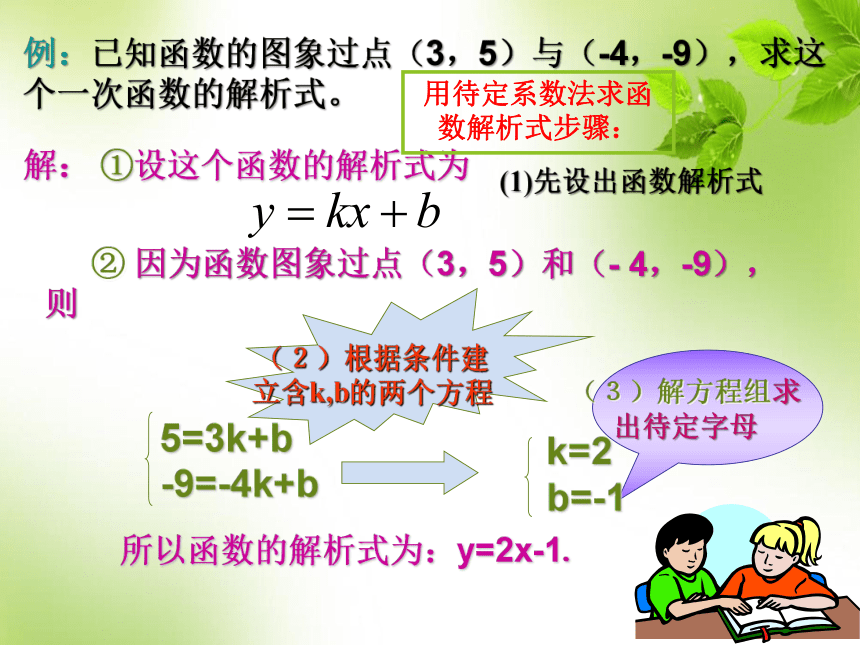
② 因为函数图象过点(3,5)和(- 4,-9),则
5=3k+b
-9=-4k+b
k=2
b=-1
例:已知函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式。
所以函数的解析式为:y=2x-1.
解: ①设这个函数的解析式为
(1)先设出函数解析式
用待定系数法求函数解析式步骤:
(2)根据条件建立含k,b的两个方程
(3)解方程组求出待定字母
先设出函数解析式,再根据条件确定解析式中未知的_____,从而得出函数解析式的方法,叫做_________.
概念:待定系数法
系数
待定系数法
归纳:用待定系数法求一次函数解析式的步骤
(1)设出一次函数解析式________;
(2)把已知条件(自变量与函数的对应值)代入 解析式得到关于待定系数的方程(组)
(3)解方程(组)求出待定系数__________;
(4)将 k、b 代入 y=kx+b,得到所求函数解析 式.
y=kx+b
k b
设
列
解
代
1.一次函数的图象经过点(2,1)和点(1,5),则这个一次函数是( )
A.y=4x+9 B.y=4x-9
C.y=-4x+9 D.y=-4x-9
C
学以致用
2、已知一次函数y=kx+b(k≠0)平行于直线 y=3x,且过点(1,4),求函数解析式
∴一次函数解析式为:y=3x+1
解: ∵一次函数y=kx+b(k≠0 )与直线y=3x平行
∴k=3
又∵一次函数y=3x+b过点(1,4)
∴3+b=4
b=1
3、在直角坐标系中,一次函数y=kx+b的图象经过三点A(2,0)、B(0,2)、C(m,3),求这个函数的关系式,并求m的值。
解: ∵一次函数y=kx+b过点A(2,0)、B(0,2),
∴
∴
∴一次函数的解析式为y=-x+2
又∵一次函数y=-x+2过点C(m,3)
∴-m+2=3 解得,m=-1 。
1、某车油箱现有汽油50升,行驶时,油箱中的余油量y(升)
是行驶路程x(km)的一次函数,其图象如图所示
求y与x的函数关系式,并写出自变量x的取值范围。
60
50
30
0
x/km
y/升
解:设函数解析式为y = kx+b,且图象过
点(60,30)和点(0,50),所以
①
②
解得
能力提升
1、已知一次函数解析式如何画它的函数图象?
函数解析式
y = kx+b
选取
满足条件的两定点
(x1,y1)与(x2,y2)
画出
一次函数的
图象:直线
选取
解出
2、已知一次函数的图象怎样求它的函数解析式?
x
y
2
-3
-4
-1
y = kx+b
从数到形
从形到数
课堂小结
待定系数法
1、通过这节课的学习,你知道利用什么方法确 定正比例函数或一次函数的解析式吗?
2、你还记得利用待定系数法确定函数解析式的一般步骤吗?
一设二列三解四写
3、体验了数形结合思想在解决函数问题作用!
2.已知一次函数的图象经过点A(2,-1)和点B,其
中点B是另一条直线 与y轴的交点,求这个一次函数的表达式。
解:设这个一次函数的解析式为y = kx+b,
由已知可知
点B是直线 与y轴交点, ∴点B(0,3)
∴一次函数y=kx+b过点A(2,-1)、B(0,3),
∴
∴
∴这个函数的解析式为y=-2x+3
课堂作业
谢谢聆听
再见
本节课学了哪些内容?
你认为最重要的是什么?
0
6
4
y
x
-3
点(0,6)
点(-3,4)
y = kx+b
4、根据图象求出函数解析式
解方程组得
k=
b=6
这个一次函数的解析式为:
3、已知一次函数y=kx-2(k≠0) ,且过点(1,3),求函数解析式
解: ∵一次函数y=kx-2( k≠0 )过点(1,3),
∴k-2=3
∴这个函数的解析式为y=5x-2
解得,k=5
学习目标:
1.掌握待定系数法,归纳用其方法求一次函数解析式的步骤。
2.具体感知数形结合思想在一次函数中的应用.
1、正比例函数 y=kx 的图象过点(-1,2),
则 k= , 该函数解析式为 .
2、右图是 函数图象,
它的解析式是 。
-2
y=-2x
0
2
4
y
x
正比例
复习回顾
② 因为函数图象过点(3,5)和(- 4,-9),则
5=3k+b
-9=-4k+b
k=2
b=-1
例:已知函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式。
所以函数的解析式为:y=2x-1.
解: ①设这个函数的解析式为
(1)先设出函数解析式
用待定系数法求函数解析式步骤:
(2)根据条件建立含k,b的两个方程
(3)解方程组求出待定字母
先设出函数解析式,再根据条件确定解析式中未知的_____,从而得出函数解析式的方法,叫做_________.
概念:待定系数法
系数
待定系数法
归纳:用待定系数法求一次函数解析式的步骤
(1)设出一次函数解析式________;
(2)把已知条件(自变量与函数的对应值)代入 解析式得到关于待定系数的方程(组)
(3)解方程(组)求出待定系数__________;
(4)将 k、b 代入 y=kx+b,得到所求函数解析 式.
y=kx+b
k b
设
列
解
代
1.一次函数的图象经过点(2,1)和点(1,5),则这个一次函数是( )
A.y=4x+9 B.y=4x-9
C.y=-4x+9 D.y=-4x-9
C
学以致用
2、已知一次函数y=kx+b(k≠0)平行于直线 y=3x,且过点(1,4),求函数解析式
∴一次函数解析式为:y=3x+1
解: ∵一次函数y=kx+b(k≠0 )与直线y=3x平行
∴k=3
又∵一次函数y=3x+b过点(1,4)
∴3+b=4
b=1
3、在直角坐标系中,一次函数y=kx+b的图象经过三点A(2,0)、B(0,2)、C(m,3),求这个函数的关系式,并求m的值。
解: ∵一次函数y=kx+b过点A(2,0)、B(0,2),
∴
∴
∴一次函数的解析式为y=-x+2
又∵一次函数y=-x+2过点C(m,3)
∴-m+2=3 解得,m=-1 。
1、某车油箱现有汽油50升,行驶时,油箱中的余油量y(升)
是行驶路程x(km)的一次函数,其图象如图所示
求y与x的函数关系式,并写出自变量x的取值范围。
60
50
30
0
x/km
y/升
解:设函数解析式为y = kx+b,且图象过
点(60,30)和点(0,50),所以
①
②
解得
能力提升
1、已知一次函数解析式如何画它的函数图象?
函数解析式
y = kx+b
选取
满足条件的两定点
(x1,y1)与(x2,y2)
画出
一次函数的
图象:直线
选取
解出
2、已知一次函数的图象怎样求它的函数解析式?
x
y
2
-3
-4
-1
y = kx+b
从数到形
从形到数
课堂小结
待定系数法
1、通过这节课的学习,你知道利用什么方法确 定正比例函数或一次函数的解析式吗?
2、你还记得利用待定系数法确定函数解析式的一般步骤吗?
一设二列三解四写
3、体验了数形结合思想在解决函数问题作用!
2.已知一次函数的图象经过点A(2,-1)和点B,其
中点B是另一条直线 与y轴的交点,求这个一次函数的表达式。
解:设这个一次函数的解析式为y = kx+b,
由已知可知
点B是直线 与y轴交点, ∴点B(0,3)
∴一次函数y=kx+b过点A(2,-1)、B(0,3),
∴
∴
∴这个函数的解析式为y=-2x+3
课堂作业
谢谢聆听
再见
本节课学了哪些内容?
你认为最重要的是什么?
0
6
4
y
x
-3
点(0,6)
点(-3,4)
y = kx+b
4、根据图象求出函数解析式
解方程组得
k=
b=6
这个一次函数的解析式为:
3、已知一次函数y=kx-2(k≠0) ,且过点(1,3),求函数解析式
解: ∵一次函数y=kx-2( k≠0 )过点(1,3),
∴k-2=3
∴这个函数的解析式为y=5x-2
解得,k=5
